Vorlesung “Modellierung 2”
Vorlesungsvideos & Lehreinheiten
Stand: 06.05.2022, 01:45
Blended Learning
Die Vorlesung wird in diesem Semester die Form einer “Blended-Learning” Veranstaltung haben. Dabei gibt es wöchentliche Treffen (“Präsenzveranstaltung”), aber die Teilnehmer/innen schauen sich vor jedem Treffen eine Vorlesung in Video-Form an. In der Präsenzveranstaltung können dann die Inhalte der Vorlesung ausführlich diskutiert werden, und es ist wesentlich mehr Interation möglich, als bei einer herkömmlichen Präsenzvorlesung.
Im folgenden finden Sie einzelne Lehreinheiten. Jede Lehreinheit entspricht einer Woche in einer konventionellen Vorlesung, wobei der Stoff in der Präsenzveranstaltung am Dienstag nach der angegebenen Bearbeitungsperiode persönlich besprochen wird.. Am Ende jeder Lehreinheit steht jeweils ein “Übungszettel”, der im Anschluss an die Präsenzveranstaltnug bearbeitet werden muss (die genaue Frist hierzu steht erst fest, wenn wir den Termin der Übungsgruppen festgelegt haben). Die Aufgaben werden nicht korrigiert, aber mit allen Teilnehmer/innen geteilt und in den Übungsgruppen besprochen.
Vorlesung in Lerneinheiten
Die Vorlesung besteht aus 14 Lehreinheiten. Für jede Lehreinheit stehen ein oder mehrere “Vorlesungs”-Videos zur Verfügung, in denen die Ideen und Hintergründe diskutiert werden.
Hinweis: Alle Videos werden auch auf dem Panopto-System der JGU gespiegelt. Anders als auf diesen Webseiten stehen die Videos dort im h264/mp4 Format zur Verfügung, das auf mehr Geräten (insbesondere Apple Safari/IPhone ohne Erweiterungen) abspielbar ist. Das Panopto System ist auch skalierbarer und kann noch genutzt werden, falls unser eigener Server die Last nicht bewältigen kann. Klicken Sie auf diesen Link, um auf die Panopto-Seite zu gelangen.
Lehreinheit 1: Wissen und Unsicherheit
(April 19 – April 25 2022)

Sokrates sagte so schön: “Ich weiß das ich nichts weiß.” – Aber was machen, wenn das nicht reicht?
-
Wie können wir Wissen aus Daten (Beobachtungen) gewinnen?
-
Wir besprechen hier den Zusammenhang von empirischem Wissen im philosophischen Sinne und den Modellen der Statistik.
Lecture:
Video: Uncertainty (73min)
Lehreinheit 2: Stochastik und Statistik
(April 26 – May 02 2022)

Mathematische Modellierung von Unsicherheit (und vor allem die nicht-mathematische Frage: Wie “darf” ich die Modelle benutzen?)
-
Als erstes gibt es eine Wiederholung von Konzepten der mathematischen Grundvorlesungen zur Statistik. Dieser Teil ist optional und dient nur zur Auffrischung des Wissens.
-
Danach sprechen wir im speziellen über den Zusammenhang von klassischer “frequentistischer” und Bayes’scher Statistik. Das ist besonders wichtig für algorithmische statistische Datenanalyse und maschinelles Lernen.
Lecture: Statistics & Stochastics Recap (69min, optional)
Video: Probability (18min)
Video: Statistical (In)dependence (21min)
Video: Moments and Measures of Distributions (30min)
Lecture: Classical vs. Bayesian Statistics (53min)
Video: Frequentist and Bayesian Statistics (53min)
Lehreinheit 3: Grundlagen statistischer Datenanalyse und Lernens
(May 03 – May 09 2022)
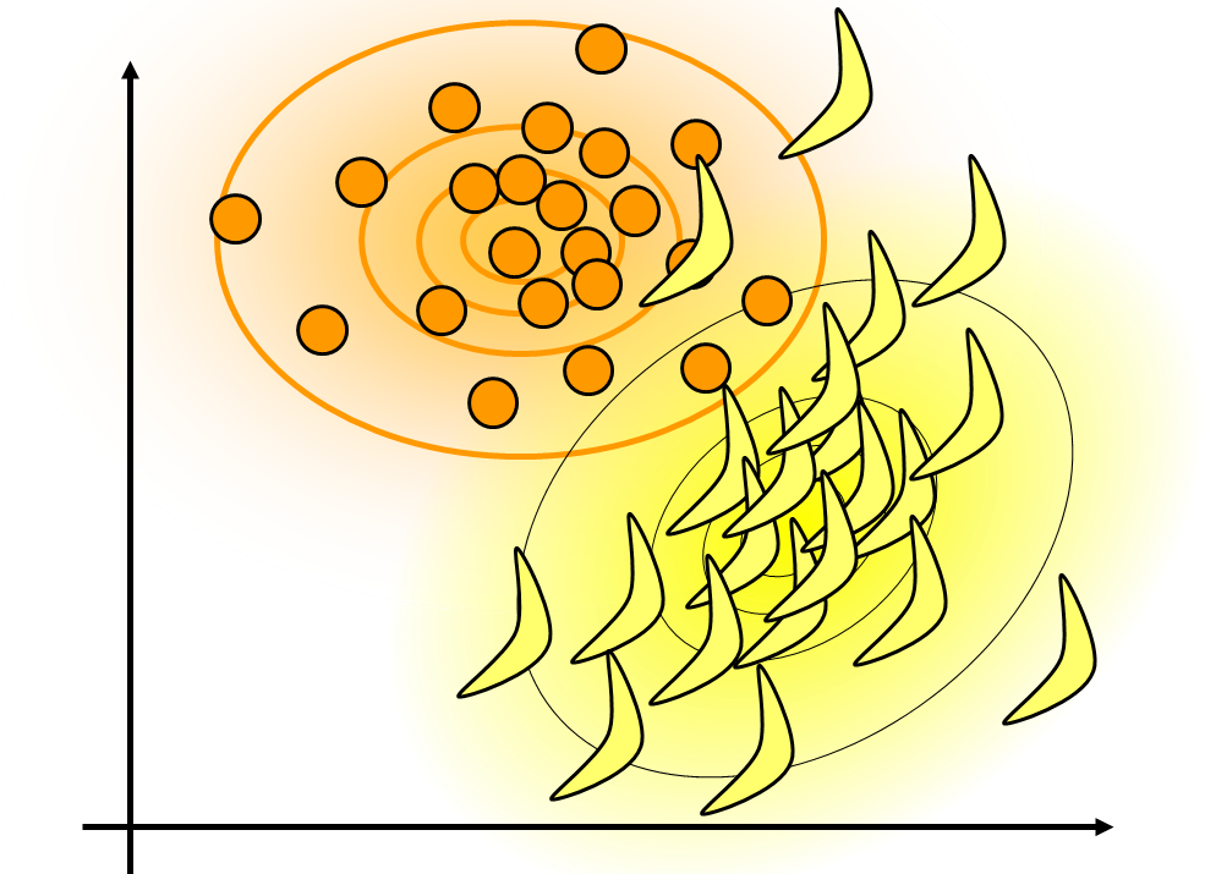
Nun benutzen wir die statistischen Werkzeuge, die wir uns zuvor erarbeitet haben, um mit mathematischen Methoden Wissen aus Daten zu extrahieren.
Wenn wir das verstehen, können wir das auch algorithmisch mit dem Computer umsetzen.
Lecture: Bayesian Data Analysis & Machine Learning (98min)
Video: Machine Learning Basics (33min)
Video: Baysian Methods for ML (35min)
Video: Learning and Inference (30min)
Hinweis: Das letzte Video “Learning and Inference” wurde am 06.05.2022 um 1:45am in einer überarbeiteten Version bereitgestellt, die das Prinzip des Bayesschen Lernens (von Modellparametern) hoffentlich klarer erklärt.
Literatur: Die folgenden Quellen, die zum Teil im Video bereits erwähnt wurden, vertiefen den Vorlesungsstoff:
- Aaron Hertzman: Introduction to Bayesian Learning. ACM Siggraph 2004 Course.
[Project Page] [Course Notes] [Course Slides]
Bemerkung: Eine kompakte und einsteigerfreundliche / praxisorientierte Einführung in Bayessche Statistik. Wenn man nicht viel Zeit zum Lesen hat, steht hier (fast) alles wichtige auf den Punkt gebracht.
- David J.C.MacKay: Information Theory, Inference, and Learning Algorithms. Cambridge University Press, 2003. Online Version.
Bemerkung: Ein sehr empfehlenswertes Lehrbuch über Bayessche Statistik, maschinelles Lernen und die Verbindung zur Informationstheorie.
- Richard O. Duda, Peter E. Hart, David G. Stork: Pattern Classification, Second Edition. Wiley, 2001.
Bemerkung: Eine einsteigerfreundliche Einführung in Bayessche Statistik und Klassifikationsalgorithmen, die darauf aufbauen. Das Buch startet mit dem Fisch-Classifier, der Vorbild für das Beispiel mit der automatischen Supermarktwaage im Video war.
Lehreinheit 4: Bayessche Datenanalyse und maschinelles Lernen – Beispiele und klassische Verfahren
(May 10 – May 16 2022)
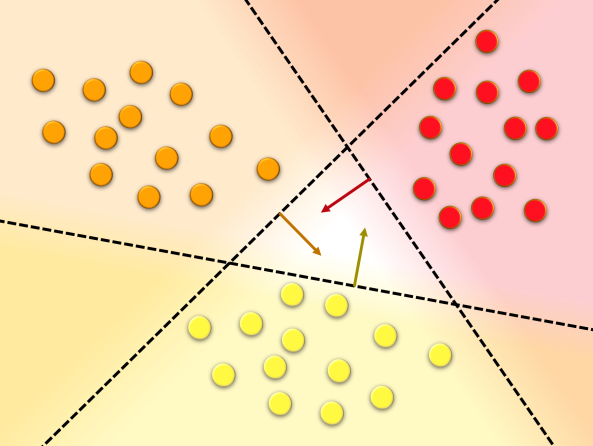
In diesem Abschnitt schauen wir uns einige Beispiele an, wie man Daten analysieren (z.B. Bildrekonstruktion) oder klassifizieren (z.B. Bilderkennung) kann.
Die Videos stellen verschiedene Beispiele zu elementaren maschinellen Lernverfahren bzw. Bayesscher Datenanalyse vor. Zwei Videos (5a,5c) greifen Beispiele auf, die bereits in Modellierung 1 ausführlich diskutiert wurden (Video 14, 16, 21).
Lecture: Bayesian Data Analysis and Classical Machine Learning (71 min + 36min optionale Wiederholung Mod-1)
Video: Gaussians, PCA, Least-Squares (Mod-1) (16min, optional)
Video: Klassische Klassifizierer (37min)
Video: Bildrekonstruktion (Mod-1) (20min, optional)
Video: Bayessche Regression (34min)
Literatur: Die folgenden Quellen, die im Video erwähnt wurden, vertiefen den Vorlesungsstoff:
Lehreinheit 6: Generalisierung I
(May 24 – May 30 2022)
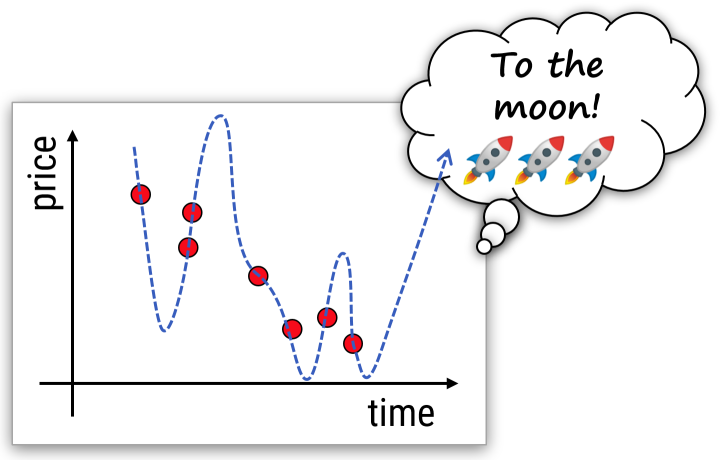
Daten fitten kann man so viel man will. Interessant ist das nur, wenn es auch auf zukünftigen Daten weiterhin funktioniert. Was wissen wir theoretisch darüber, ob das möglich ist, und können wir voraussehen, ob es klappen wird?
Dieser Abschnitt ist vielleicht der wichtigste der ganzen Vorlesung, denn er stellt die Frage, ob (bzw. wann) das ganze überhaupt Sinn macht. Die Argumente sind eigentlich sehr simpel, aber es geht wohl um den Kern der Sache.
Wir starten mit zwei grundlegenden (und nur scheinbar widersprüchlichen) Ergebnissen: Das Mittagessen ist nie umsonst, und Bias und Varianz kann trotzdem man gegeneinander ausspielen. Die Videos erklären, was das alles soll:
Lecture: Generalisierung (79 min)
Video: The No-Free Lunch Theorem (27min)
Video: Statistical Learning Theory: Bias-Variance Trade-Off (61min)
Literatur: Nachlesen kann man das alles nochmal hier
Lehreinheit 7: Generalisierung II
(May 31 – June 06 2022)

Nun geht es an die etwas technischeren / subtilen Aspekte des Problems (dennoch von zentraler Bedeutung):
- Wie kann man Occam’s Rasiermesser formalisieren? (hier am Beispiel mit Informationstheorie – es gibt noch diverse andere Ansätze)
- Warum macht Bayes’sche Inferenz über mehrere Modellvarianten das (mehr-oder weniger) automatisch?
Dieses Video ist wahrscheinlich das wichtigste der ganzen Vorlesung.
tl;dr – Bayes’sche Inferenz ist schon toll (wenn auch leider meist ziemlich teuer). Hier gibt es mehr:
Lecture: Generalisierung II (80 min)
Video: Bayesian Model Selection (80min)
Bemerkung: Gleicher Foliensatz für LE06 + LE 07.
Literatur: Die Hingergründe sind technisch etwas anspruchsvoller. Daher ist es hier besonders zu empfehlen, die Quellen genau zu lesen, auf denen das Video basiert.
- Als erstes geht es um MDL. Die zentrale Quelle dazu ist:
Peter Grunwald: A tutorial introduction to the minimum description length principle. https://arxiv.org/pdf/math/0406077.pdf, 2004.
- Eingangs wurden auch allgemeinere Coding-Length-Ansätze mit universellen Maschinen angesprochen, siehe hierzu z.B.: Materialien von J. Schmidhuber zu universellen Lernalgorithmen (mit weiteren Quellen) und dem Speed-Prior.
- Der Zusammenhang von MDL und Bayes’scher Inferenz wird im Buch von D. MacKay gut erklärt (Kapitel IV-28):
David J.C.MacKay: Information Theory, Inference, and Learning Algorithms. Cambridge University Press, 2003. Online Version.
Bemerkung: Grunwald widerspricht der Einstellung zu einem gewissen grade; siehe daher auch die Diskussion dazu in der ersten Quelle.
- Wer noch tiefer einsteigen möchte: MacKay erwähnt, dass Bayes’sche Inferenz mit Modellgewichtung “echte” Priors braucht. Die folgende Quelle erklärt, wo es sonst schiefgehen kann:
A.P. Dawid, M. Stone, J.V. Zidek: Critique of E.T. Jaynes’s “Paradox of Probability Theory”, https://www.ucl.ac.uk/drupal/site_statistics/sites/statistics/files/rr172.pdf, 2003.
Hinweis: Nach aktueller Planung ist das folgende Kapitel nicht Teil der Vorlesung. Änderungen sind im Laufe des Semesters noch möglich.
Optionales Kapitel: Markov’sche Modelle
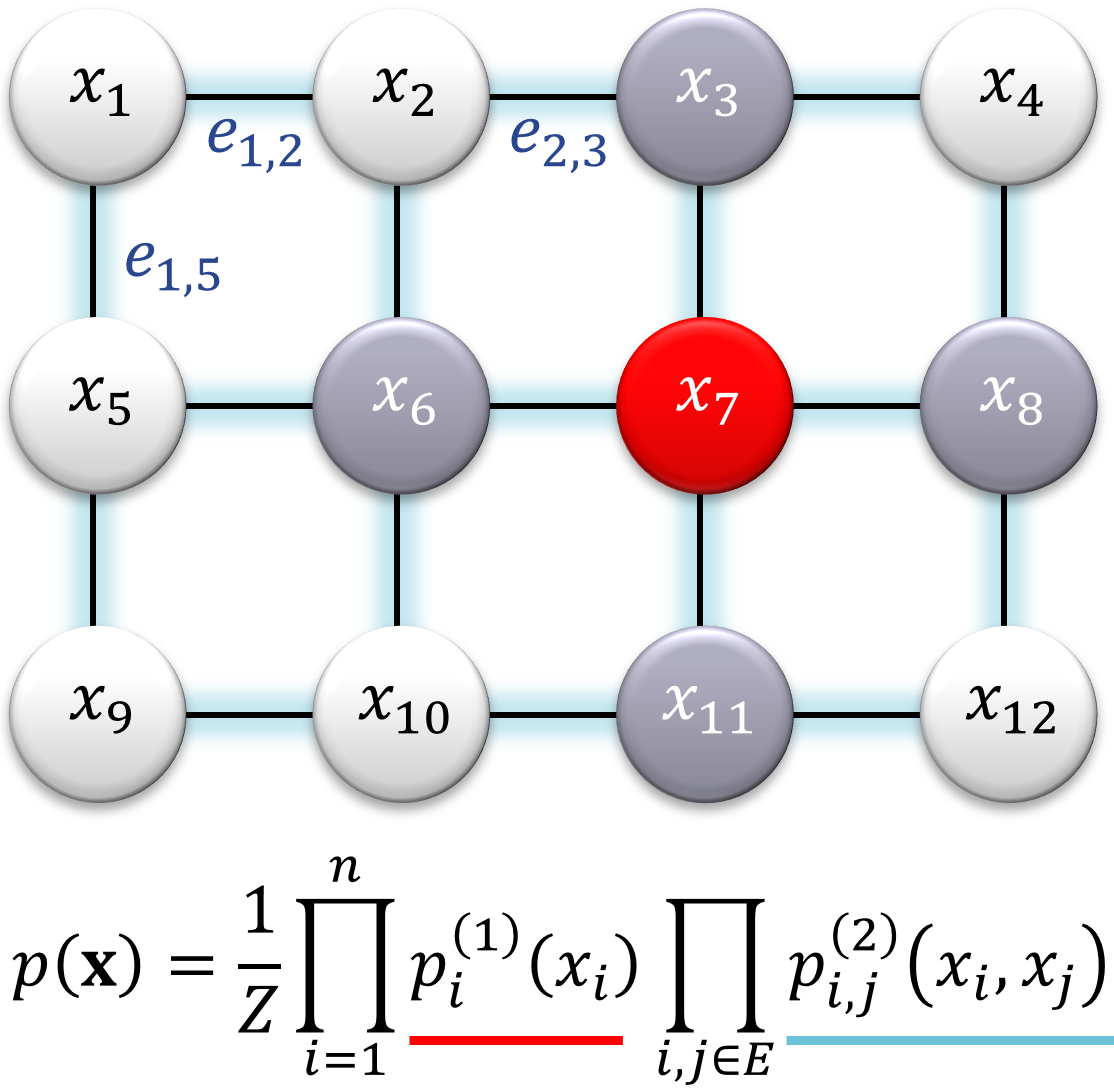
Oft ist es sinnvoll statistische Abhängigkeiten einzuschränken. Eine wichtige Klasse von Modellen sind Markov-Random-Fields (mit Markovketten als Spezialfall). Hier hängen Zufallsvariablen nur von direkten zeitlichen oder räumlichen Nachbarn ab.
Diese Modelle sind besonders wichtig für die Modellierung physikalischer Systeme, bei denen elementare Wechselwirkungen immer mit der unmittelbaren räumlichen und zeitlichen Nachbarschaft stattfinden.
Man kann die Idee auch approximativ auf Systeme anwenden, die das “nur so ungefähr” erfüllen. Naja, wie immer halt.
Lecture: Markovsche Modelle (101min)
Video: Markov Ketten (17min)
Video: Hidden Markov Models (27min)
Video: Markov Random Fields (57min)
Lehreinheit 8: Grundlagen tiefer Netze
(June 07 – June 13 2022)
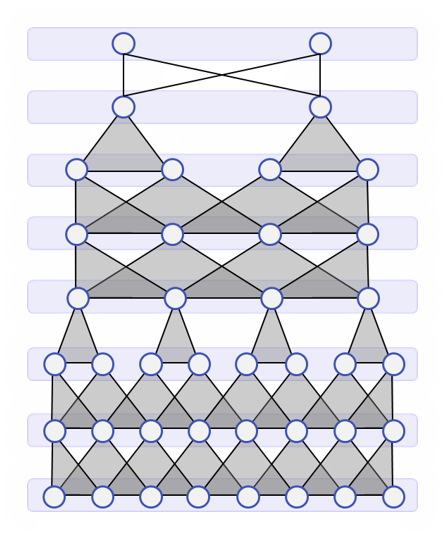
Nun schauen wir uns Deep Learning an, die Technik die uns den jüngsten KI-Sommer beschert hat.
In diesem Teil geht es erstmal um die Grundlagen und einige Beispielarchitekturen.
Stack moah’ layers! (reddit)
Lecture: Deep Learning (96min)
Video: Deep Learning Basics (43min)
Video: Deep Learning Methods and Architectures (53min)
Hinweis: Die Videos auf Folie 80/81 sind in der aktuellen Fassung sehr ruckelig – die Orginale kann man
hier anschauen (externer Link auf Youtube).
Hinweis: Hier beginnen die “fortgeschrittenen”, “forschungsnäheren” Themen; entsprechend sind noch kurzfristige Änderungen für alle Lehreinheiten ab LE09 möglich auch im späteren Verlauf der Veranstaltung noch möglich.
Lehreinheit 9: Generative Modelle auf Basis tiefer Netze
(June 14 – June 20 2022)

Als ein (wichtiges und interessantes) Beispiel für komplexere Techniken für die Modellierung tiefer Netze schauen wir uns das Problem an, generative Modelle zu lernen. Das heißt, wir möchten aus Beispielen eine Wahrscheinlichkeitsverteilung rekonstruieren, um diese danach für allerlei Anwendungen einsetzen zu können. Was auf den ersten Blick nach einen recht harmlosen und grundlegenden Problem klingt, entpuppt sich als doch ziemlich herausfordernd.
Lecture: Generative Deep Networks (95min)
Video: Generative Deep Networks (95min)
Bemerkung: Generative Modelle im Foliensatz für LE09 enthalten.
Literatur: Mehr zu GANs:
- Blog Artikel mit Übersicht über GAN und WGAN (und vielen weiteren Quellen): Lillian Weng: From GAN to WGAN, https://lilianweng.github.io/lil-log/2017/08/20/from-GAN-to-WGAN.html
- Tero Karras, Timo Aila, Samuli Laine, Jaakko Lehtinen: Progressive Growing of GANs, ICLR 2018 [paper], [code].
Diese Arbeit ist nicht nur die Grundlage der derzeit besten GAN-Implementierungen – das Paper enthält auch eine sehr gut Anleitung, wie man ein (W-)GAN stabil trainieren kann. Wenn man den Schritte im Paper genau folgt, sollte es funktionieren.
- Karras et al.: ProGAN, StyleGAN, StyleGAN2,… – Eine Übersicht über State-of-the-Art GAN Methoden von diesem Team.
Beispiel für Normalizing Flows:
Lehreinheit 10: Distanzen, Sampling, Kernels
(June 21 – June 27 2022)
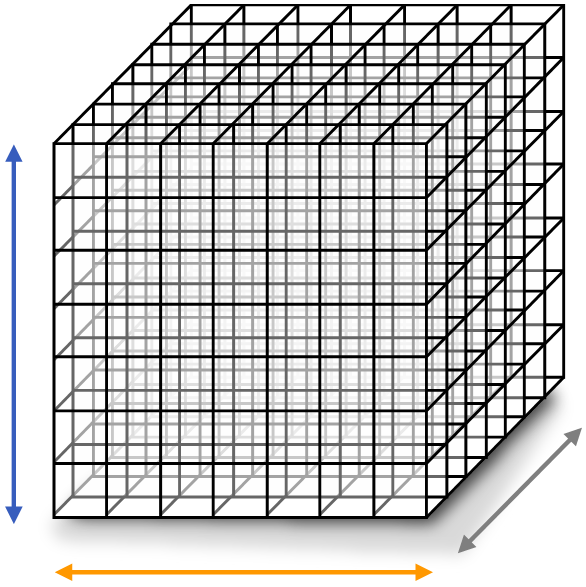
Dieses Mal wollen wir besser verstehen, warum viele klassische Lernverfahren nicht funktionieren können, und wo wir zumindest wissen, dass tiefe Netze mehr Potential bieten: Wir schauen uns die Limitierungen distanz-basierter Lernverfahren an, indem wir das mit Samplingtheorie in Verbindung bringen.
Danach steigen wir in Kernelverfahren ein: Was, wenn wir doch einfach nur die Distanz anpassen müssen (und ganz allgemein ist das etwas, was auch ein tiefes Netzwerk macht)? Hier schauen wir uns die Grundlagen dazu an.
Vorschau: Beim nächsten Mal benutzen wir das dann, um verblüffende Eigenschaften von tiefen Netzen in einem einfachen, approximativen Kernel-Modell zu erklären.
Lecture: Zwischenstand (11min)
Video: Deep Learning ist also magic; was nun? (11min)
Abschließend fassen wir nochmal zusammen, was wir bislang gelernt haben, und wo die großen offenen Fragen sind (auch als Motivation & Ausblick auf das letzte Drittel der Vorlesung). Wie können wir besser verstehen, warum (künstliche) neuronale Netzwerke eigentlich funktionieren?
Lecture: Distances, Sampling, and kernels (74min)
Video: The Curse of Dimensionality (28min)
Video: Algorithms for High Dimensions (19min)
Video: Kernel methods (bis 27min / Folie 71). (27min)
Bemerkung:Das letzte Video zu Kernel Methoden brauchen Sie für die Diskussion diese Woche nur bis Minute 27 anschauen (Folie 71). Gauß’sche Prozesse machen wir nächstes Mal.
Außerdem ein Hinweis: Die Folien für diese und die nächsten beiden Lehreinheiten sind derzeit in einer Datei zusammengefasst.
Literatur: Der Fluch der hohen Dimension. Außerdem: Kernels
- Hoch-dimensionale Räume
- Kernel-Methoden
Lehreinheit 11: Gaußsche Prozesse
(June 28 – July 04 2022)

Ein Spezialfall von Kernelmethoden sind “Gaußsche Prozesse”. Sie verallgemeinern eigentlich nur das Konzept von least-squares-fitting mit Basisfunktionen, wie wir es aus Modellierung 1 (oder LE04 in dieser Vorlesung) kennen auf den Fall unendlich-dimensionaler Basen.
Das ist nicht nur an sich ganz praktisch; es hilft auch dabei, komplexere Systeme wie tiefe Netzwerke zu modellieren und Analysieren. Die Ergebnisse sind durchaus überraschend.
Wir schauen uns nun an, wie man GPs baut, und wie man damit einige der Geheimnisse des tiefen Lernens lüften kann.
Lecture: Gaussche Prozesse (53min)
Video: Kernel Methods & Gaussian Processes (53min; ab 27min / F. 72)
Bemerkung:Das Video zu bitte ab Minute 27 (Folie 72) weiterschauen (Fortsetzung von LE10).
Hinweis: Die Folien für die vorherige, diese und die nächste Lehreinheit sind derzeit in einer Datei zusammengefasst.
Literatur: Gaussche Prozesse & Analyse von tiefen Netzen:
- Gaussche Prozesse Allgemein
- Analyse von DNNs / Netzwerke als GPs
- R.M. Neal: Bayesian Learning for Neural Networks. Springer-Verlag, 1996. https://www.cs.toronto.edu/~radford/ftp/pin.ps
- C. Zhang, S. Bengio, M. Hardt, B. Recht, O. Vinyals: Understanding deep learning requires rethinking generalization. ICLR 2017. https://arxiv.org/pdf/1611.03530.pdf
- A. Achille, S. Soatto: Emergence of Invariance and Disentanglement in Deep Representations. Journal of Machine Learning Research 18 (2018) 1-34. https://arxiv.org/pdf/1706.01350.pdf
- M. Belkin, D. Hsu, S. Ma, S. Mandal: Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proc. of the National Academy of Sciences 116 (32), 15849-15854, 2019. https://arxiv.org/pdf/1812.11118.pdf
- P. Nakkiran, G. Kaplun, Y. Bansal, T. Yang, B. Barak I. Sutskever: Deep Double Descent: Where Bigger Models and More Data Hurt. ICLR 2020. https://openreview.net/forum?id=B1g5sA4twr
- Bayesian Model Averaging for DNNs
Lehreinheit 13: Physik I: Symmetrie
(13 July 12 – July 18 2022)
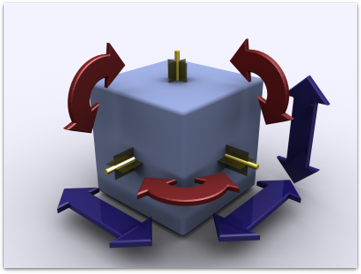
Empirische Wissenschaften beschäftigen sich seit Jahrtausenden damit, Modelle der Welt zu bauen; hier können wir uns sicherlich ein paar Tricks abschauen. Besonders nah an unseren Bedürfnissen (mathematisch, reduktionistisch, in der Regel simulier- und implementierbar) sind die Ideen der Physiker.
Gehen wir also Ideen sammeln bei den theoretischen und statistischen Physikern. Als erstes fällt uns die Idee der Symmetrie in die Hände.
Lecture: Zur Einstimmung ins Thema: Übersicht Physik (53min, optional)
Video: Kurzüberblick: Physikalische Modelle aus Informatiksicht (53min)
Einordnung: Das Video ist nützlich um insbesondere die letzte Lehreinheit (LE14) zu verstehen. Der Stoff ist nicht prüfungsrelevant, da es nicht um Informatikthemen geht.
Lecture: Symmetrie (74min)
Video: Symmetrie ist nicht vorhandene Information (16min)
Video: Etwas Gruppentheorie (34min)
Video: Equivarianz – strukturerhaltende Änderungen (24min)
Literatur: Zur Symmetrie
- Mary Phuong, Christoph H. Lampert: Functional vs. parametric equivalence of ReLU networks. ICLR 2020. https://openreview.net/forum?id=Bylx-TNKvH
Das Paper diskutiert, welche unterschiedlichen ReLU Netzwerke die selbe Funktion berechnen können. Für diese Repräsentationssymmetrie gibt es (vielleicht überraschend) relativ wenige Freiheiten.
- Taco S. Cohen, Max Welling: Group Equivariant Convolutional Networks. ICML 2016. https://arxiv.org/abs/1602.07576 Das Paper erklärt, wie man CNNs zu Netzwerken verallgemeinern kann, die unter allgemeinen Symmetriegruppen equivariant sind.
- Allan Zhou, Tom Knowles, Chelsea Finn: Meta-learning Symmetries by Reparameterization. ICLR 2021. https://openreview.net/pdf?id=-QxT4mJdijq
Das Paper zeigt eine Methode, mit der man Symmetrien für ein Netzwerk lernen kann.
- Crystallographic Space Groups: Wikipedia – alle zweihundernd-und-ein-paar verschiedenen Strukturen für Kristalle (Raumgruppen), und die wilde Geschichte, wie sie entdeckt wurden. Bonus: Dann hat noch jemand 5-fache Rotationssymmetrie gefunden, die es beweisbar nicht geben kann. Quasikristalle
- Niloy J. Mitra, Mark Pauly, Michael Wand, Duygu Ceylan: Symmetry in 3D Geometry: Extraction and Applications. Eurographics State-of-the-Art-Report, 2012.
Ein Survey-Paper aus der Computergraphik über Symmetrie, mit einem etwas pragmatischeren und algorithmischem Ansatz. Aus alten Zeiten :-)
Lehreinheit 14: Physik II: Emergenz
(14 July 19 – July 23 2022)
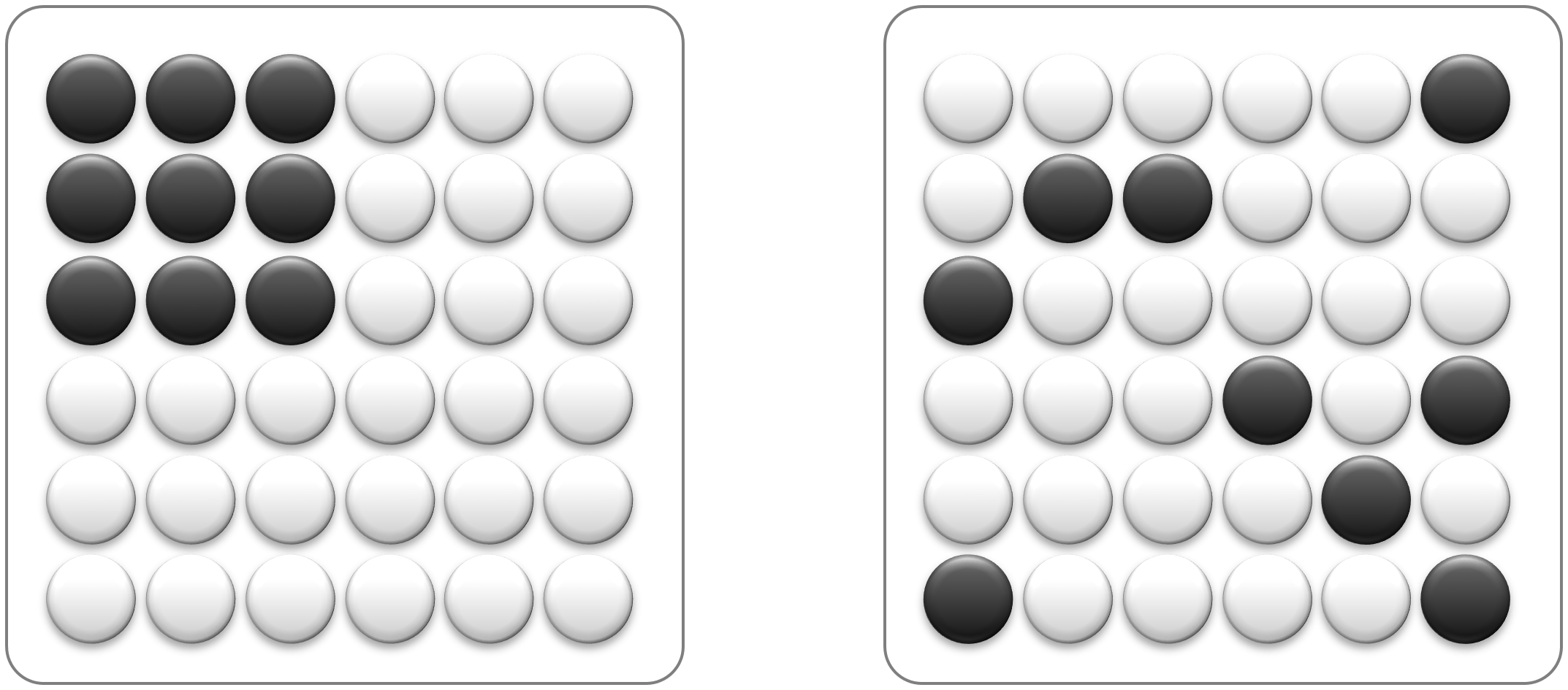
Was uns besonders interessiert, sind effektive Theorien: Wir haben ein System aus unglaublich vielen kleinen Bestandteilen, und wir verstehen auch ungefähr, was die machen (wobei wir nicht alle Details genau messen können).
Was wir aber nicht wissen, ist was das ganze Ding im Groben so ungefähr machen wird. Statistische Datenmodellierung und statistisches Lernen versucht in der Regel ein solches Problem zu beantworten: Ist das eine Katze - ja oder nein? Egal, wie genau die Pixel aussehen.
Die statistiche Physik beschäftigt sich mit dem Problem, wie aus unwichtigen, mikroskopischen Details, die bekannten physikalischen Gesetzen folgen, gröbere, beobachtbare Strukturen entstehen. Hier ein erster Einstieg in die Methoden, die man sich dort abschauen kann.
Lecture: Self-Organization & Emergent Structure (62min)
Video: Self-Organization & Emergent Structure (62min)
Übungsaufgaben: Zur letzten LE gibt es keine Übungsaufgaben mehr.
Zusammenfassung/Rückblick: Zum Schluss gibt es noch ein kurzes Video mit einem Rückblick auf alle Vorlesungsinhalte, das dazu dienen soll, den Stoff insgesamt nochmal einzuordnen.
Lecture: Zusammenfassung und Rückblick (10min)
Video: Concluding Remarks (10min)
Literatur: Physik + ML
- Henry W. Lin, Max Tegmark, David Rolnick: Why does deep and cheap learning work so well? Journal of Statistical Physics volume 168, pages 1223–1247, 2017. https://arxiv.org/abs/1608.08225
Das Paper stellt genau die Fragen aus dem Video, und gibt einige Analysen, aber wohl keine endgültige Antwort. Trotzdem sehr zu empfehlen.
- Daniel A. Roberts, Sho Yaida, Boris Hanin: The Principles of Deep Learning Theory: An Effective Theory Approach to Understanding Neural Networks. Cambridge University Press 2022. Online: https://arxiv.org/abs/2106.10165
Hier wird noch tiefer in die Trickkiste der theoretischen Physik gepackt, mit erstaunlichen Einsichten.
Datenschutz
Impressum