Institut für Informatik
Modellierung 2
Michael Wand
David Hartmann
Sommersemester 2021 • DIGITAL
Aufgabe: Forward Pass
Wir starten mit dem Problem. Gegeben ein einfacher 2D-Datensatz, bestehend aus jeweils wenigen Klassen von Punkten. Wir wollen ein Neuronales Netz entwerfen, das solche Datenssätze selbstständig zu klassifizieren lernt.
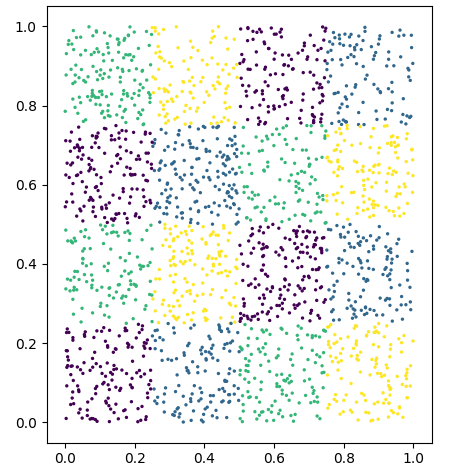



Als Datensatz dient uns entweder ein selbstgebauter Datensatz, beispielsweise ein Gitter mit einer festen und ungefähr gleichverteilte Anzahl an Klassen (siehe Bild) oder aber einer der vorgefertigten Spielzeug-Datensätze von SciKit-Learn.
Wichtig: Damit Sie gute Ergebnisse erziehlen müssen Sie vorher dafür sorgen, dass der Datensatz normiert in das Netz kommt, d.h. den Mittelwert 0 hat bei einer Standardabweichung von 1.
Wir schauen uns Netze der Form \[
f(x) := \left(f_n \circ a \circ f_{n-1} \circ a \circ \dots a \circ f_2 \circ a \circ f_1\right)(x)
\] an, wobei \(a\) die oben beschriebene ReLU-Aktivierungsfunktion ist und \(f_i\) Lineare Layer mit den jeweiligen Parametern \(W_i \in \mathbb{R}^{c_{i-1}\times c_{i}}\) und \(b_i\in \mathbb{R}^{c_i}\).
Wir starten mit zufällig gewählten Parametern. Konkret wählen wir \(W_i \sim \mathcal{N}(0,1)\) und \(b=0.1\).
Aufgabe: Implementieren Sie den Forward-Pass, d.h. eine Auswertung des Netzes auf einem Datenpunkt \(x\).
Hinweise:
- Wir können hier die parallelisierbarkeit des Matrix-Vektorproduktes ausnutzen indem wir die Operationen direkt für mehrere Datenpunkte implementieren, also für einen Datentensor der Dimension \(n\times 2\).
- Versuchen Sie ruhig verschiedene Anzahlen von Layern. Wichtig hierbei ist lediglich, dass die letzte Operation des Netzes keine Aktivierungsfunktion ist.
- Implementieren Sie auch die Bewertung des aktuellen Netzwerkstadiums; die Softmax-Cross-Entropie der Ausgabe stellt dabei eine Ableitbare Energiefunktion dar, die Accuracy, die wir bereits in Lehreinheit 4 kennen gelernt haben gibt uns den Anteil an richtig klassifizierten Datenpunkten zurück.
Aufgabe: Backward Pass / BackProp
Nun zur Optimierung. Wir schauen uns die Cross-Entropie der Ausgabe des Netzwerks an, \(y(x) := \operatorname{SingleClassSoftmaxCE}(f(x), y)\). Die Frage, wie wir die Gewichte ändern müssen, damit sich die Energiefunktion (a.k.a. Loss) lokal verbessert, lässt sich leicht Beantworten: Die Ableitung zeigt in die Richtung des steilsten Anstiegs. Wir haben in Lehreinheit 8 bereits verschiedene Algorithmen kennengelernt, die diese Idee zur Optimierung nutzen.
Der einfachheit Halber implementieren wir Stochastic Gradient Descent:
Um den Loss zu minimieren gehen wir einfach eine strikte Distanz \(W_i \rightarrow \lambda \cdot \nabla \frac{\partial y}{\partial W_i}\).
Doch wie erhalten wir diese Gradienten effizient? Die Antwort darauf zeigt uns die Kettenregel. Wir leiten den Loss nach einem beliebigen Gewicht mitten im Netzwerk ab. \[ \frac{\partial y}{\partial W_i} = \frac{\partial \operatorname{SCSCE}}{\partial f_n} \cdot \frac{\partial f_n}{\partial a} \cdot \frac{\partial a}{\partial f_{n-1}} \cdot \dots \cdot \frac{\partial f_{i+1}}{\partial a} \cdot \frac{\partial a}{\partial f_i} \cdot \frac{\partial f_i}{\partial W_i} \]
Die Faktorisierung der Ableitung durch die Kettenregel ermöglicht es uns den folgenden Algorithmus.
Für jeden Layer im Netzwerk berechnen wir die lokale Ableitung des Ergebnisses nach den Eingaben und nach den Gewichten. Für einen linearen Layer \(f_i(x) := x\cdot W_i + b_i\) ist dies einfach (siehe auch hier): \[ \begin{align} \frac{\partial f_i}{\partial W_i} &:= x\\ \frac{\partial f_i}{\partial x} &:= W_i^T\\ \frac{\partial f_i}{\partial b_i} &:= 1 \end{align} \]
Aufgaben:
- Wie sieht das im Fall der Aktivierungsfunktion \(a\) aus und im Falle des Softmax-CrossEntropy-Losses?
- Um also ein spezifisches Gewicht \(W_i\) anzupassen, müssen wir zuerst den Loss bestimmen und dann der Kettenregel folgend alle Faktoren bis zum Layer \(f_{i+1}\) aufmultiplizieren und zuletzt mit \(W_i^T\) multiplizieren. Das Ergebnis skaliert mit \(\lambda\) können wir direkt auf die Gewichte anwenden. Praktischerweise ändern sich die Multiplikationen für alle folgenden Layer nicht, d.h. wir können eine Menge Rechnungen sparen.
- Implementieren Sie die ganze Optimierungspipeline und plotten Sie die Verläufe von Loss und Accuracy.
- Testen Sie verschiedene Netz-Größen (Anzahl Layer, Anzahl Dimensionen \(c_i\) auf den verschiedenen Layern) und verschiedene Batch-Größen (also die Anzahl an Punkten, die bei jedem Forward-/Backwardpass neu gewürfelt werden).
Aufgabe: Visualisierung
Die starke Expressivität der Neuronalen Netze kommt von den Nichtlinearitäten. (Falls wir uns alle nichtlinearen Layer im oben beschriebenen Netzwerk \(f\) wegdenken würden, könnten wir nämlich alle linearen Teile in einen einzigen linearen Layer zusammenfassen. In der Vorlesung wurde erklärt, wie ein Neuronales Netz den Eingaberaum in Zellen unterteilt und es so schafft in verschiedenen Bereichen des Eingaberaumes unterschiedliche Rechnungen durchzuführen. Wir dies hier nachimplementieren.
- Zeigen Sie, dass ein Neuronales Netz ohne Aktivierungsfunktionen durch einen einzigen linearen Layer dargestellt werden kann.
- Wir definieren ein festes Gitter von 2D-Punkten, zum Beispiel \(\{(h,w) |h,w \in \{-5,-4.9,-4.8,\dots\}\}\). Wir können dies Beispielsweise als Bild verstehen, das wir per
matplotlib.plt.imshowdarstellen können. - Nun zur Farbe: Wir möchten die Zellen „sehen“, in die das Neuronale Netz den Eingaberaum unterteilt. Dazu inferieren alle Zwischenergebnisse bis Layer \(i\).
Konkret schauen wir uns also zuerst das Zwischenergebniss des \(i\)-ten linearen Layers an, \[ y_i(x) := \left(f_{i} \circ a \circ \dots a \circ f_2 \circ a \circ f_1\right)(x). \] Dadurch, dass im nächsten Layer die Aktivierungsfunktion alle Komponenten, die kleiner als 0 sind auf 0 setzt, können wir die Zellen messen, indem wir alle Punkte gleich einfärben, die das selbe Aktiviergunsmuster \(\operatorname{sign}(y_i(x)) \in \{-1,1\}^{c_i}\) haben. (Den Fall, dass wir die 0 genau treffen ignorieren wir).
Färben Sie die Pixel des Bildes nach den Aktiviergunsmustermustern. (Also alle Pixel mit dem Muster \({-1,1,-1,...}\) gelb, alle Pixel mit dem Muster \({1,1,1,...}\) grün, usw. - Was ist der Grund, dass der in 3. beschriebene Algorithmus Voronoi-artige Zellen aufzeigt? (Schauen Sie dazu noch einmal in die Vorlesungsvideos rein.)
- Was können Sie beobachten?
- In der Initialisierung des Netzwerkes (noch keine Optimierung geschehen?)
- Im fertig trainierten Netz?
- Wie verhält sich die Visualisierung während des Trainings?
- Insbesondere: Was ist der Anteil an mit Daten gefüllten Zellen zur Anzahl an möglichen Zellen?
