---

---

Aufgabe 5.1: 2D-Ableitung

[20 Punkte]

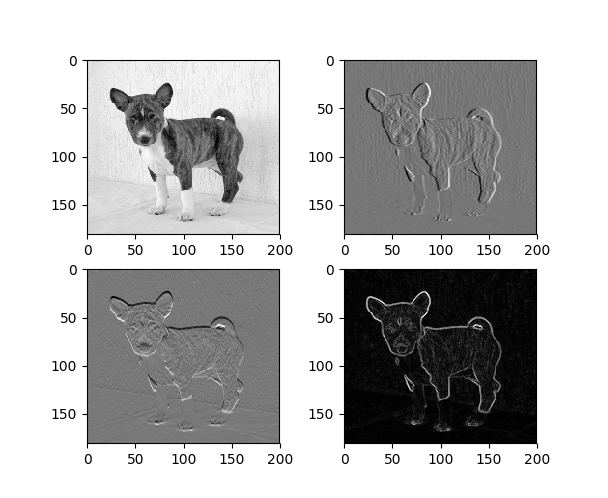
Trotz der Schwächen der numerischen Ableitung, die wir auf dem letzten Blatt beobachten konnten, gibt es viele praktische Anwendungen. Neben der offensichtlichen — der Abschätzung der Ableitung eines gemessenen Datensatzes — können wir die Ableitung auch auf Bilder anwenden!
Wir berechnen dazu den Gradientenvektor in Bildern, wie folgt: Analog zum obigen eindimensionalen Fall definieren wir die numerischen Richtungsableitungen im zweidimensionalen Raum als \[\begin{aligned} \frac{d}{dx}f(x,y) &:\approx \frac{f(x+h,y) - f(x-h,y)}{2h} \qquad \text{und}\\ \frac{d}{dy}f(x,y) &:\approx \frac{f(x,y+h) - f(x,y-h)}{2h}. \end{aligned} \] (Man kann hier auch eine unsymmetrische Version, wie auf dem letzten Aufgabenblatt nehmen.)
Mathematisch tun wir so, als wäre die Funktion eindimensional und leiten wie gewohnt ab, und betrachten alle Terme, die von der jeweils anderen Variable abhängen als Konstanten. Was wir erhalten, ist eine zweidimensionale Größe: den Gradientenvektor. Die Länge gibt an, wie Stark der Wert der Funktion sich an der Stelle ändert, und die Richtung zeigt in die Richtung des stärksten Anstiegs.
Anmerkung: Wir benutzen hier, der Einfachheit halber, nur einfache Differenzenquotienten mit endlich kleinem \(h\) (in der Regel wählt man \(h=1\text{ Pixel}\)); wenn die Bilder stark verrauscht sind, müssten wir erst filtern bzw. am besten ein 2D-MLS-Schema verwenden. Das geht im Prinzip genauso wie im 1D Fall, wird uns hier aber zu aufwendig. Also nur Bilder ohne zuviel Rauschen!

Aufgabe

• Lesen Sie ein Graustufen-Bild ein und zeigen Sie dieses an. Im Skript erklären wir Ihnen wie Sie dies auch leicht mit Matplotlib realisieren können (siehe das für dieses Aufgabenblatt neu geschriebene Kapitel 1.3.10 „Bild mit Matplotlib visualisieren.“ im Skript). Alternativ können Sie (auch ohne ein aufwendiges GUI zu erstellen) als QImage mit einem QLabel anzeigen lassen.
  
  Hinweis:
  Eine Sammlung von Graustufenbildern können Sie beispielsweise mit Google-image finden (suchen Sie z.B. nach „grayscale image“), oder man nimmt GIMP/Paint.net/Photoshop und entfernt die Farbe aus einem Farbbild (wie man Bilder ohne QT einliest, steht auch in Kapitel 1.3.10 im Skript erklärt).
• Bestimmen Sie nun die Richtungsableitungen des Bildes in \(x\)- bzw. \(y\)-Richtung.
• Visualisieren Sie nun das Bild, die Richtungsableitung und auch die Länge der Ableitungen \(\sqrt{\frac{d}{dx}f^2 + \frac{d}{dy}f^2}\) in einem einzigen Plot (siehe obige Abbildung).
  
  Hinweis:
  (Im Skript wurde ein Eintrag im Matplotlib-Unterkapitel angefügt wie sie mehrere Plots zusammenfassen können. Siehe: Subplots)
• Was können Sie beobachten? Was tun die Richtungsableitungen und was erkennt man mithilfe der Länge der kombinierten Ableitung?

Numerische Integration von Differentialgleichungen

Im zweiten Teil dieses Aufgabenblattes möchten wir zeitabhängige Differentialgleichungen lösen. Dies sind Gleichungen, die die Ableitungen einer Funktion und die Funktion selbst enthalten. Somit ist die Funktion selbst als Variable zu betrachten.

Hinweis: Lesen Sie Kapitel 6.1-6.3 im Skript durch, um die Theorie zu erarbeiten, die man für die Lösung dieser Aufgaben braucht.

Motivation: Auf dem letzten Übungsblatt wollen wir diese Konzepte dazu verwenden, ein Spiel zu programmieren, in dem die dynamische Flugbahn von Wurfgeschossen berechnet werden soll (es war von lat. Annelida die Rede). Hier üben wir schonmal das Prinzip.

Aufgabe 5.2.1: Das Federpendel
(a.k.a.: „harmonischer Oszillator“)

[20 Punkte]

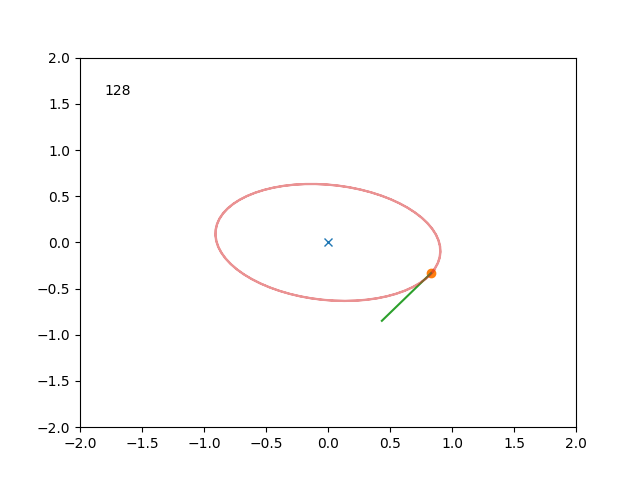
Unser erstes Beispiel ist ein Federpendel: Wir nehmen an, dass eine Masse an einer Feder hängt. Bei einer Hookschen (linearen) Feder, was für echte Federn durchaus realistisch ist, ist die Rückholkraft ist proportional zur Auslenkung \(x\), allerdings mit negativem Vorzeichen. Wir beschreiben die Rückholkraft \(F\), die einen Körper zum Ursprung zurück zieht, durch \[F = -Dx, \quad D > 0, \] wobei \(x\) die aktuelle Position und \(D\) eine positive Konstante ist. Mithilfe des zweiten Newtonschen Gesetzes \(F=ma\) (\(a\) beschreibt die Beschleunigung, \(m\) die Masse des Objektes) und der Einsicht \(a(t)=x''(t)\) können wir die Gleichung zu
\[x''(t) = -\frac{Dx(t)}{m} \] und weiter zu dem System
\[\frac{d}{dt} \left( \begin{array}{c} x(t) \\ x'(t) \end{array} \right) = \left( \begin{array}{c} x'(t) \\ -\frac{Dx(t)}{m}\\ \end{array} \right) \]

umschreiben (siehe Skript!). Unter der Annahme, dass diese Kraft zu jedem Zeitpunkt auf das Objekt an der Stelle \(x\) wirkt, haben wir die Position durch eine Funktion \(x(t)\) ersetzt.

Numerische Lösung von Differentialgleichungen: Für eine feste Funktion können wir stets symbolisch Prüfen, ob sie die Differentialgleichung erfüllt oder nicht. Beispielsweise ist die Null-Funktion \(x(t)=0\) eine Funktion, die die obige Gleichung erfüllt (dies ist eine Lösung für ganz spezielle Anfangsbedingungen, nämlich keine initiale Auslenkung und keine initiale Geschwindigkeit). Es gibt jedoch weitaus mehr; z.B. gibt es mathematische Tools, um symbolisch die Familie von Funktionen zu finden, die eine solche Differentialgleichung erfüllen. Im Allgemeinen ist dies jedoch eine schwierige Aufgabe.
Glücklicherweise können wir uns jedoch der Lösung numerisch nähern: Wir starten mit einer Startbelegung zum Zeitpunkt \(t=0\) (z.B. \(x(0) = c\)). Wir wissen bereits, wie wir die Ableitung einer Funktion numerisch bestimmen können (siehe letztes Übungsblatt), nämlich durch den Differenzenquotienten zweier aufeinanderfolgender Stadien unseres Systems \(x_t\) und \(x_{t+1}\), \[x'(t) \approx \frac{x(t)-x(t+h_t)}{h_t} \]

unter der Annahme, dass die Stadien \(h_t\) Zeiteinheiten entfernt sind. Der Einfachheit halber können Sie annehmen, dass die Zeit stets gleichmäßig abläuft, \(h_t = h, h\in \mathbb{R}\). Falls wir also bereits die Ableitung kennen, können wir durch Umstellen der Gleichung sogar den neuen Status des Systems extrapolieren: \[x(t+h) = x(t) + x'(t)\cdot h. \] Dieses Wissen können wir nun verwenden, um eine einfache physikalische Simulation zu programmieren.

Aufgabe

• Schreiben Sie ein Programm, mit dem Sie (z.B. mit Matplotlib) einen Punkt in der Ebene anzeigen lassen können und seine Position nachträglich verändern können. Sie können dabei gerne insbesondere das im Skript angeführte Beispiel in Kapitel 1.3.11 „Animieren mit Matplotlib“ als Anhaltspunkt zum Animieren des Plots verwenden.
• Definieren Sie eine zufällige Startbelegung. Die obige Differentialgleichung zum Harmonischen Oszillator liefert uns ausgehend von der Position die Beschleunigung. Mithilfe von dieser können wir die Geschwindigkeit auf den nächsten Zeitschritt extrapolieren. Um jedoch die Position auch auf den nächsten Zeitschritt extrapolieren möchten, benötigen wir also auch Startbelegungen für die Geschwindigkeit. Der Einfachheit halber können Sie annehmen, dass die Position \(x\) und die Geschwindigkeit \(x'\) jeweils in \([-1,1]^2\) enthalten sind.
  
  Hinweis: Indem wir komponentenweise rechnen (dies geschieht automatisch, wenn Sie die Rechnungen auf Numpy-Arrays ausführen), wurde die eindimensionale Gleichung auf zwei Dimensionen erweitert. Alternativ können Sie auch zwei getrennte Gleichungen, jeweils für die \(x\)- und \(y\)-Richtung, definieren.
• Verwenden Sie die Differentialgleichung, um aus dem aktuellen Status die aktuelle Beschleunigung zu bestimmen.
  
  Wenden Sie nun eine Euler-Integration an, um aus der aktuellen Geschwindigkeit die Position des Folgeschrittes und aus der aktuellen Beschleunigung die Geschwindigkeit des Folgeschrittes zu bestimmen.
• Erstellen Sie einen Timer (z.B. per QTimer, der das Lösen der Differentialgleichung, das Anwenden des Integrationschrittes und die Aktualisierung des Plots übernimmt. Starten Sie nun die Simulation.)
• Zeichnen Sie auch den Geschwindigkeitsvektor vom Punkt \(x\) aus und den insgesamt zurückgelegten Weg.

Aufgabe 5.2.2: einfache Pendelgleichung

[20 Punkte]

Ein weiteres Beispiel einer Differentialgleichung ist die Pendelgleichung unter Gravitation in einem isolierten System \[\alpha''(t) = -\frac{g}{l} \sin(\alpha(t)).\]

Erklärung der Gleichung:

Die Funktion \(\alpha(t)\) beschreibt die Auslenkung des Pendels zum Lot zur Zeit \(t\) (siehe Abbildung, \(\alpha=0\) entspricht einem ruhigen Pendel).

Der Term \(\frac{d^2}{dt^2} \alpha(t) =: \alpha''(t)\) beschreibt dabei die zweite Ableitung von \(\alpha\), \(l\) die Länge des Lots, \(g\) die Erdanziehungskraft (\(g=9.81 \frac{m}{s^2}\)).
Die Gleichung beschreibt, wie sich die Auslenkung im Allgemeinen über die Zeit verhält. Physikalisch gesprochen beschreibt sie, dass die Winkel-Beschleunigung \(\alpha''(t)\) davon abhängt wie stark das Pendel in \(x\)-Richtung ausgelenkt ist.

Die Gleichung ist ganz ähnlich zum Federpendel aus der vorherigen Aufgabe; bei kleiner Auslenkung verhält es sich fast genauso (weil \(\sin(x) \approx x\) für kleine \(x\)); bei größeren Auslenkungen wird die Gleichung nichtlinear, weil die Rückholkraft immer nur in Richtung Erde zeigt, und dieser Richtungsvektor dreht sich nicht mit dem Pendel mit. Dramatisch anders sieht die Lösung allerdings, wie Sie sehen werden, nicht aus.

Aufgabe

• Starten Sie wieder damit, dass sie das System als solches beispielsweise in Maptlotlib darstellen können. (Zeichnen Sie dabei das Lot, die Kugel und auch den Fixpunkt des Lots ein).
• Simulieren Sie nun wie in der Aufgabe davor die Pendelbewegung.
• Sie werden beobachten, dass durch die Euler-Integration, die lediglich eine approximative Lösung darstellt schnell Energie in das System kommt (das Pendel bewegt sich immer schneller). Die kann beispielsweise durch bessere Methoden (wie das Runge-Kutta-Verfahren) gelöst werden. Die Verfahren unterscheiden sich hauptsächlich darin, wie sie die numerische Ableitung verrechnen; z.B. als Ableitung des aktuellen Schrittes oder als Ableitung des nächsten Schrittes.
  
  Eine weitere (nicht ganz akkurate) Lösung ist es, die Physik kontrolliert zu stören, indem man die Geschwindigkeit insgesamt durch eine Multiplikation mit einer konstante \(c\in (0,1]\) langsam dämpft.
  Implementieren Sie dies.

Aufgabe 5.2.3: Doppelpendelgleichung

[20 Punkte]

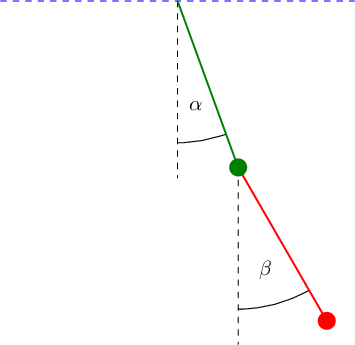
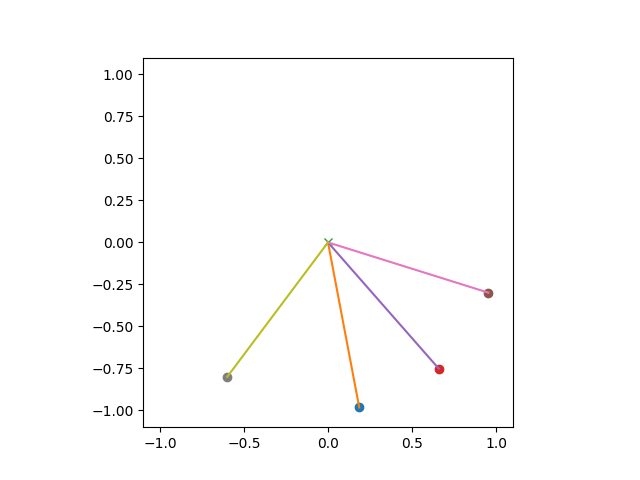
Etwas interessanter ist es zwei zusammenhängende Pendel zu betrachten, da sich hier die beiden Pendel gegenseitig beeinflussen. Wir definieren die Winkel \(\alpha,\beta\) wie in der Abbildung.
Die Doppelpendelgleichung lautet \[ \begin{aligned} \alpha'' &= -\frac{g}{l_1}\sin \alpha - \frac{l_2m_2}{l_1(m_1+m_2)}\left( \cos(\alpha - \beta)\beta'' + \sin(\alpha - \beta)\cdot(\beta')^2\right) \\ \beta'' &= -\frac{g}{l_2}\sin \beta - \frac{l_1}{l_2}\left( \cos(\alpha - \beta)\alpha'' - \sin(\alpha - \beta)\cdot(\alpha')^2\right) \\ \end{aligned} \]

Im Grunde sollte Implementierung mithilfe der letzten Aufgabe schnell zu realisieren sein. Ziel ist es, einzusehen, dass Differentialgleichungen schnell chaotisches Verhalten aufweisen können und meist numerisch instabil sind.

Aufgabe

• Starten Sie wieder damit, dass sie das System als solches beispielsweise in Matplotlib darstellen können. (Zeichnen Sie dabei beide Fäden, die Kugeln und auch den Fixpunkt des gesamten Pendels ein).
• Simulieren Sie nun wie in den beiden Aufgaben davor die Pendelbewegung. Sie werden schnell merken, dass diese Differentialgleichung um ein Vielfaches instabiler ist, als die einfache Pendelgleichung. Wir können auch hier wieder bessere Verfahren anwenden oder dämpfen (wobei das gedämpfte System ein ganz anderes Verhalten hätte). In diesem Fall berechnen wir die Simulation einfach genauer:
  
  Berechnen Sie in jedem Animationsschritt mehrere Integrationsschritte und zeigen diesen jedoch nur als einen an. Falls die Simulation dennoch zu langsam abläuft, können Sie auch alternativ die Simulation (also die resultierenden Positionen) vorausberechnen, und später aus einer Liste ablesen und als Animation abspielen.
• Das Doppelpendel kann als chaotisch erklärt werden: sehr kleine Änderungen der Startbelegung können zu immensen Änderungen nach nur wenigen Schritten führen. Dieses Video zeigt dies für ein Dreifach-Pendel. Wenn sie möchten können Sie dies auch mit Ihrem Code leicht nach implementieren. Berechnen Sie statt einem Pendel mehrere (im Video sind es 41) und geben Sie jeder Trajektorie eine andere Farbe mithilfe der Color-Map-Methode, die auf dem letzten Blatt erklärt wurde. Verschieben Sie die Startbelegungen nun sukzessive und minimal.

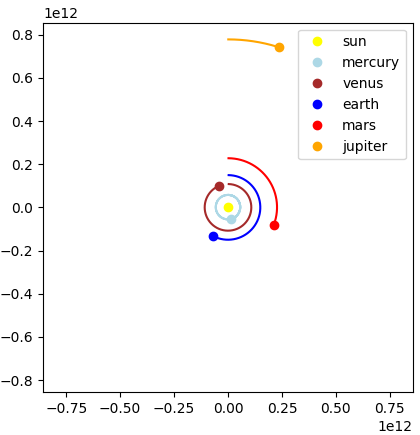
Aufgabe 5.2.4: Simulation des Sonnensystems

[20 Punkte]

Wir betrachten die Gleichung \[F = \gamma_0 \frac{m_1\cdot m_2}{r^2},\]

die die Anziehungskraft zwischen zwei Objekten mit den Massen \(m_1\) bzw. \(m_2\) erklärt. Die Variable \(r\) bezeichne dabei den Abstand zueinander und \(\gamma_0 \approx 6,674 \cdot 10^{-11} \frac{m^3}{kg\cdot s^2}\) die Gravitationskonstante. Zusammen mit \(F=ma\) können wir daraus schließen, dass das Objekt mit der Masse \(m_1\) die Beschleunigung \[x''(t) = a(t) = \gamma_0 \frac{m_2}{r^2},\] in Richtung des Objektes mit der Masse \(m_2\) aufweist.

Wir nutzen dies, um die Bewegungen des Sonnensystems zu simulieren.

Aufgabe

• Entnehmen Sie der angegebenen Tabelle die Masse der Sonne, die Massen der ersten fünf Planeten, die (mittlere) Entfernungen zur Sonne und ihre (mittlere) Bahngeschwindigkeit.
  
  Hinweis: In der Gravitationskonstante kommt \(m^3\) vor, die Geschwindigkeiten und die Entfernungen jedoch in \(km\); vereinheitlichen Sie dies vorher. Hinweis: Python erlaubt die wissenschaftliche Notation, z.B. a = 123.45e-23 für \(123,45\cdot 10^{-23}\)
• Implementieren Sie die Startbelegung ihres Sonnensystems: Startposition, Startgeschwindigkeit, Massen.
  (Um es leichter zu machen, dürfen sich die Planeten zu Beginn auf einer Linie befinden.).
  
  Hinweis: Es lohnt sich die Daten in Listen, etwa \[ M = [ m_\text{merkur}, m_\text{venus}, m_\text{erde}, \,\dots ], \] statt einzelnen Variablen zu speichern, damit wir leicht beliebig viele Objekte anlegen können. Dies werden wir nämlich später benötigen.
• Implementieren Sie nun die nötigen Funktionalitäten, um mithilfe von Matplotlib das System zu visualisieren und wie vorher auch mit einer Update-Funktion zu aktualisieren.
• Implementieren Sie den einen Euler-Integrationsschritt zur Auflösung der Anziehungskraft zwischen den Planeten und der Sonne, und visualisieren Sie die sukzessive Anwendung.
• Asteroiden: Fügen Sie \(100\) Asteroiden in der Nähe von \(r=400\cdot 10^9 \pm 30\cdot 10^9 m\), den ungefähren Massen \(m=0.00001\cdot 10^{24}\) und den Bahngeschwindigkeiten von ca. \(v=18217 \text{ m/s}\) ein. Beobachten Sie, was passiert! Was sagt uns das über den Asteroidengürtel?
  
  Python: Wie üblich können Sie mit np.random.random() Zufallszahlen generieren.
• Optional: Implementieren Sie außer der Anziehung zur Sonne auch alle paarweisen Anziehungen zwischen den Planeten. Was sollte sich ändern?
• Optional: Fügen Sie ihrem System den Mond hinzu. Der Abstand zwischen Mond und Erde ist ziemlich gering im Vergleich zum Abstand zwischen Erde und Sonne; wenn das System stabil ist, sollten Sie sehen, dass der Mond in der Umlaufbahn der Erde bleibt.