Analysis II - Differentialgleichungen

Die Infinitesimalrechnung (Differential- & Integralrechnung) war ursprünglich physikalisch motiviert. In diesem Kapitel schauen wir uns daher mal grob an, wie man dynamische Phänomene (also die Bewegung von Dingen) mit Differentialgleichungen modellieren kann. Wir bleiben dabei eng an der Praxis, und beschränken uns auf einfache Simulationsprobleme (Anfangswertprobleme). Das brauchen wir, um die letzte Praktikumsaufgabe lösen zu können.

Newtonsche Mechanik

Wie bereits im vorherigen Kapitel 5 angedeutet, ist die Ableitung ein Modell, dass eine Antwort auf eine Frage aus der Physik gibt: Wir stellen uns vor, dass die Welt sich mit der Zeit verändert. Wie sich die Zukunft entwickelt, ist vollständig in jedem Zeitpunkt kodiert. Anders gesagt: Wenn wir alles über den Zustand der Welt zu einem festen Zeitpunkt wissen, dann ist die gesamte Zukünftige Entwicklung eindeutig bestimmt. Alle physikalischen Modelle gehorchen bis heute im Wesentlichen dieser Idee (wobei man für gekrümmte Raumzeiten in der Relativitätstheorie etwas vorsichtig sein muss, wenn man fragt, was ein Zeitpunkt ist, und in der Quantenphysik werden Aussagen probabilistisch; das Prinzip ändert sich aber nicht grundlegend).

Nehmen wir die klassische Mechanik als Beispiel: Herr Newton macht einen Spaziergang über eine Obstwiese (diese Geschichte ist wohl nur eine Legende) und sieht, wie ein Apfel vom Baum fällt. Wir können den Zustand des Apfels ganz einfach als Abstand über dem Boden beschreiben. Dieser Zustand ändert sich natürlich kontinuierlich, über die Zeit:

\[{\color{red}x}: \mathbb{R} \rightarrow \mathbb{R};\, \,\,\, {\color{darkblue}t} \text{ [Zeit]} \mapsto {\color{red}x}({\color{darkblue}t}) \text{ [Hoehe]}\]

Mit diesem Modell beschreiben wir die gesamte Geschichte unserer Welt, indem wir die Koordinaten aller relevanten Objekte (Apfel; hier: Höhe über Grund in Metern) als Funktion über die Zeit modellieren. Der Wert dieser Funktion zu einem festen Zeitpunkt beschreibt den aktuellen Zustand der Welt.

Dieses Modell hat leider ein Problem: Wir können nicht unterscheiden zwischen einem Apfel, der in die Luft geworfen wurde, und einem Apfel, der gerade von einem Baum fällt. Was fehlt, ist die „Bewegung“ in den Zustand mit aufzunehmen. Die Geschwindigkeit, mit der sich ein Objekt gerade, momentan bewegt, gehört anscheinend inhärent zum „aktuellen Zustand“ der Welt. Lässt man dies weg, so bekommt man kein sinnvolles Modell (nichts bewegt sich). Wir können dieses Problem lösen, indem wir die Änderung der Position des Apfels über die Zeit als weitere Variable aufnehmen:

\[\text{Zustand der Welt: } {\color{red}x},{\color{red}v}: \mathbb{R} \rightarrow \mathbb{R}\\ {\color{darkblue}t} \text{ [Zeit]} \mapsto {\color{red}x}({\color{darkblue}t}), {\color{red}v}({\color{darkblue}t}) \text{ [Hoehe, Fallgeschwindigkeit]}\]

Die Geschwindigkeit, \({\color{red}v}({\color{darkblue}t})\), ist genau die Änderung des Ortes über die Zeit, das heißt:

\[\frac{d}{d{\color{darkblue}t}}{\color{red}x}({\color{darkblue}t})= {\color{red}v}({\color{darkblue}t})\]

Dies ist eine Differentialgleichung (engl. differential equation): Die Position des Apfels ändert sich mit der Zeit. Wenn wir vorgeben, wie sich die Geschwindigkeitsfunktion verhält (möglicherweise in Abhängigkeit von Zeit \({\color{darkblue}t}\) und aktueller Position \({\color{red}x}({\color{darkblue}t})\)), dann können wir eine Lösung ausrechnen.
In unserem Beispiel wissen wir, dass die Geschwindigkeit linear ansteigt: Zum Zeitpunkt 0 (Apfel beginnt Fall) ist die Geschwindigkeit 0, danach wächst der Betrag gleichmäßig mit \(9.81\frac{m/s}{s}\) (wir messen alle Längen in Metern, und alle Zeiten in Sekunden; außerdem bezeichnen wir die Geschwindigkeit als negativ, da sich die Höhe des Apfels beim Fallen verringert, nicht erhöht):

\[{\color{red}v}({\color{darkblue}t}) = -9.81 \cdot {\color{darkblue}t}\,\,\,\, ({\color{darkblue}t} \ge 0)\]

Warum das so ist, sehen wir etwas später; natürlich ist die Funktion \({\color{red}v}\) selbst Lösung einer Differentialgleichung. Man sollte auch festhalten, dass dieses Beispiel sehr einfach ist, da die Ableitung des Ortes (also die Funktion \({\color{red}v}\)) nicht vom Ort selbst abhängt. Aber als einleitendes Beispiel ist das ganz ok.

Lösung von Differentialgleichungen (Anfangswertprobleme)

Lösung der Gleichung (numerisch)

Wir können jede solche Differentialgleichung sehr einfach näherungsweise numerisch lösen. Das ganze geht in drei Schritten:

• Theorie: Als erstes nehmen wir an, dass alle Funktionen, mit denen wir es hier zu tun haben, glatt sind \(C^\infty\). Für eine stetig differenzierbare Funktion \({\color{red}x}({\color{darkblue}t})\) wissen wir, dass diese in einem kleinen, lokalen Bereich \([{\color{darkblue}t}-\epsilon, {\color{darkblue}t}+\epsilon]\) beliebig genau durch eine einfache Grade angenähert werden kann.
  • Steigung ausrechnen: Naja, dann nutzen wir das: Nehmen wir an, wir kennen den Systemzustand \({\color{red}x}({\color{darkblue}t})\) zu einem Zeitpunkt \(\color{darkblue}t\). Dann können wir die Steigung der Funktion \({\color{red}v}({\color{darkblue}t})\) einfach ausrechnen.
  • Ein Schritt weitergehen: Nun nutzen wir, dass die Funktion näherungsweise linear weiterverläuft. Für einen kleinen Schritt \(\epsilon\) können wir also einfach folgendes rechnen:

\[{\color{red}x}({\color{darkblue}t}+\epsilon) \approx {\color{red}x}({\color{darkblue}t}) + \epsilon \cdot {\color{red}v}({\color{darkblue}t}) \] Das ganze kann man dann iterieren: Wir haben jetzt einen neuen Wert, an dem können wir wieder die Steigung bestimmen, und einen Schritt gehen, usw. Diesen Vorgang bezeichnet man auch (etwas verwirrend) als numerische Integration (engl. numerical integration) einer Differentialgleichung. In dem hier angeführten Beispiel ist dieser Name übrigens sehr treffend; da \({\color{red}v}({\color{darkblue}t})\) nicht von der aktuellen Posution \({\color{red}x}({\color{darkblue}t})\) abhängt, berechnen wir tatsächlich genau das Integral. Man nennt dies aber auch sonst Integration (auch wenn man mehr als ein Integral für die Lösung braucht; es ist sozusagen eine Verallgemeinerung der Integration).
Das hier erklärte Verfahren ist als explizites Eulerverfahren (engl. explicit Euler integrator) bekannt.

Lösung der Gleichung (symbolisch)

Unsere Beispielgleichung ist so einfach, dass wir sie auch analytisch Lösen können. Man sieht, dass wir eigentlich nur die Stammfunktion von \({\color{red}v}({\color{darkblue}t})\) berechnen müssen; deren Ableitung ist genau das gesuchte \({\color{red}x}({\color{darkblue}t})\). Anders gesagt:

\[{\color{red}x}({\color{darkblue}t}) = {\color{red}x}({\color{darkblue}0}) + \int_0^x{{\color{red}v}({\color{darkblue}t})d{\color{darkblue}t} = 9.81 \cdot \frac{1}{2} \cdot {\color{darkblue}t}^2} \]

Der Anfangswert \({\color{red}x}({\color{darkblue}0})\) ist genau diejenige Höhe über Grund, die der Apfel hat, wenn er seinen Fall beginnt. Die Geschwindigkeit zu diesem Zeitpunkt ist in unserem Modell (realistischerweise) null.

Gleichungen höherer Ordnung

Das ganze hat noch einen Haken: Woher kennen wir eigentlich den Verlauf der Geschwindigkeitsfunktion? Die ist hier (no pun intended) einfach vom Himmel gefallen.

Newton hatte die Idee, dass Objekte durch Kräfte beschleunigt werden. Wie stark ein Objekt beschleunigt, hängt aber nicht nur von der Kraft ab, die wirkt, sondern auch von der Masse des beschleunigten Objektes. Wir kennen das aus dem Alltag: Autoschieben beschleunigt schlechter als Fahrradschieben bei gleicher Kraft (gib alles). In Newtons Modell ist die Beziehung wie folgt:

\[{\color{red}a}(t) = \frac{{\color{red}F}(t)}{m}\]

Hierbei gibt die Funktion \({\color{red}a}\) die Beschleunigung eines Objektes an, und \(m\) ist seine Masse (die Formel ist auch besser bekannt als „\({\color{red}F} = m \cdot {\color{red}a}\)“ ).
Wie zuvor ist die Beschleunigung (per Definition) genau die Ableitung der Geschwindigkeit:
\[\frac{d}{d{\color{darkblue}t}}{\color{red}v}({\color{darkblue}t})= {\color{red}a}({\color{darkblue}t})\]

Damit können wir berechnen, wie die Geschwindigkeit sich ändert, und damit auch, wie die Position sich ändert (wir machen zwei Schritte im expliziten Eulerverfahren; eine Schätzung der neuen Geschwindigkeit in Abhängigkeit der Kräfte; danach eine Schätzung der neuen Position gemäß der aktualisierten Geschwindigkeit.

Damit haben wir fast ein vollständiges Modell; wir müssen nur noch beschreiben, wie die Kräfte entstehen. Um Äpfel zu Boden fallen zu lassen, oder auch Planeten und Sonnen umeinander kreisen zu lassen, benutzt man das newtonsche Gravitationsgesetz:

\[{\color{red}F}({\color{darkblue}t})=\gamma_0 \cdot \frac{m_1 \cdot m_2}{{\color{red}r}({\color{darkblue}t})^2}\]

Dabei sind \(m_1,m_2\) die Massen der beiden beteiligten Objekte (üblicherweise gemessen in kg; in unserem Beispiel: Apfel und Planet Erde) und \({\color{red}r}\) die Distanz (der Mittelpunkte) der beiden beteiligten Objekte (normalerweise in Metern). \(\gamma_0 \approx 6,674 \cdot 10^{-11} \frac{m^3}{kg\cdot s^2}\) ist die Gravitationskonstante (in Einheiten von Meter, Sekunden, und kg). Diese Konstante gibt in unserem Universum an, wie stark die Gravitationskraft wirkt. In der Tat ist die Kraft relativ schwach; man braucht schon planetare Objekte, bevor etwas größeres passiert. Die Kraft wirkt natürlich auf beide Objekte (Erde und Apfel); die Beschleunigung der Erde kann man aber in diesem Beispiel getrost vernachlässigen (die Masse \(m\) im Nenner vom \(F=a/m\) sorgt dafür, dass hier praktisch nichts passiert).

Wir können nun unser Modell etwas generischer Schreiben, indem wir überall die Ableitungen einsetzen, die die Größen \({\color{red}v},{\color{red}a}\) eigentlich definieren:

\[{\color{red}a}({\color{darkblue}t}) := \ddot{{\color{red}x}}({\color{darkblue}t})\\ {\color{red}v}({\color{darkblue}t}) := \dot{{\color{red}x}}({\color{darkblue}t}) \]

Damit bekommen wir insgesamt das folgende Gleichungssystem:

\[ \begin{aligned} \ddot{{\color{red}x}}({\color{darkblue}t}) &= {\color{red}F}({\color{darkblue}t},{\color{red}x}({\color{darkblue}t}))\\ \dot{{\color{red}x}}({\color{darkblue}t}) &= \frac{d}{d{\color{darkblue}t}}{\big[\color{red}x}({\color{darkblue}t})\big] \text{ (trivial)} \end{aligned} \]

Die zweite Gleichung lässt man in der Regel weg. Sie dient hier nur zur Erinnerung, dass wir den Zustand des Ortes dadurch einen kleinen Zeitschritt \(\epsilon\) weiterschreiben können, indem wir \(\epsilon \cdot \dot{{\color{red}x}}({\color{darkblue}t})\) darauf addieren. Das selbe machen wir zuvor mit der Beschleunigung \(\ddot{{\color{red}x}}({\color{darkblue}t})\) und der Geschwindigkeit \(\dot{{\color{red}x}}({\color{darkblue}t})\) und können so (näherungsweise) die Lösung bestimmen.

In der Mathematik schreibt man eine solche Gleichung zweiter Ordnung (engl. second order differential equation) kurz als:

\[\begin{aligned} \ddot{{\color{red}x}}({\color{darkblue}t}) &= {\color{red}F}({\color{darkblue}t},{\color{red}x}({\color{darkblue}t})) \end{aligned} \]

Eine Gleichung \(n\)-ter Ordnung entspricht aber immer einem System von \(n\) Gleichungen, bei denen immer nur eine Funktion und deren Ableitung betrachtet werden (genauso wie in unserem Beispiel). Der Systemzustand besteht dann aus den \((n-1)\) niedrigeren Ableitungen. In der klassischen Mechanik sind alle Gleichungen zweiter Ordnung; Kräfte, die vom Systemzustand abhängen, bestimmen die Beschleunigung, und die ist die zweite Ableitung der Position(en).

Um eine solche Gleichung konkret lösen zu können, müssen wir Anfangsbedingungen (engl. initial conditions) vorschreiben. Die Differentialgleichung (11) bzw. (13) beschreibt nur die Dynamik, also den weiteren Verlauf unseres Systems; um eine feste Lösung (Orts- und Geschwindigkeitsfunktion, müssen wir vorgeben, in welchem Zustand das System losläuft. Das sieht man schön, wenn man sich den numerischen Integrator (expliziter Euler) anschaut; dieser startet ja in einem festen Zustand — danach ist die Lösung berechenbar. Diesen Startzustand nennt man genau die Anfangsbedingungen.

\[ \begin{aligned} \dot{{\color{red}x}}({\color{darkblue}0}) &= {\color{red}0} \text{ (Apfel war gerade noch fest.)}\\ {\color{red}x}({\color{darkblue}0}) &= {\color{red}{\text{Baumhöhe}} } \end{aligned} \]

Man beachte hier nochmal, dass der Zustand einer DGL n-ten Grades genau aus den unteren Ableitungen vom Grad \(0\) (Position selbst) bis \(n-1\) (hier: Grad 1, entspr. Geschwindigkeit) besteht; entsprechend müssen wir genau diese Information am Anfang festsetzen.

Allgemeine Systeme von gewöhnlichen Differentialgleichungen

Höhere Dimensionen

Unser Modell hat noch einen wichtige Einschränkung: Bislang können wir nur ein einziges Objekt modellieren, und für dieses auch nur eine skalare Größe; hier z.B. die Höhe des Apfels über Grund. Reale Systeme haben aber oft viele Freiheitsgrade (z.B. die allgemeine Bewegung eines Objektes im Raum — die hätte 3 Freiheitsgrade. Bewegen sich \(n\) Objekte, hätten wir \(3n\) Freiheitsgrade).

Grundidee: Die Grundidee ist ganz einfach: Wir sammeln einfach mehrere Variablen, die Positionen beschreiben (Koordinaten komponentenweise). Das selbe machen wir für Ableitungen (wieder komponentenweise). Danach „integrieren“ wir die Ableitungen auf (auch komponentenweise), ausgehend von einem Startzustand (bei dem jede Komponente von allen Variablen und deren niedrigeren Ableitungen auf einen Anfangswert initialisiert sind).

Nehmen wir die klassische Mechanik als Beispiel: Wir haben eine Menge von Punkten gegeben (z.B. die Sonne und die 8 Planeten). Die Positionen aller \(n\) Objekte in diesem System sind \(n \times 3=9\times 3 = 27\)-dimensional:

\[(({\color{red}x}_1,{\color{red}y}_1,{\color{red}z}_1), ({\color{red}x}_2,{\color{red}y}_2,{\color{red}z}_2), ..., ({\color{red}x}_n,{\color{red}y}_n,{\color{red}z}_n)) \in \mathbb{R}^{3n}\]

(Die Klammern in dem großen Tupel sind nur Verzierung, damit man sieht, was zusammengehört. Vektoren (aka. Tupel) von Vektoren sind auch nur bloß große Vektoren). Der Einfachheit halber schreiben wir im folgenden die Sammlung aller Tripel von x-,y- und z-Koordinaten als Vektor \(\mathbf{\color{red}x}\); fett gedruckt heißt hier „Vektor“, also die Sammlung aller Koordinaten:

\[({\mathbf{\color{red}x}}_1, {\mathbf{\color{red}x}}_2, ..., {\mathbf{\color{red}x}}_n) \in (\mathbb{R}^{3})^n = \mathbb{R}^{3n}\]

Die Geschwindigkeit, mit der sich ein Objekt gerade bewegt, gehört auch hier wieder inhärent zum „aktuellen Zustand“ der Welt. Also nehmen wir alle Ableitungen der Positionen nach der Zeit auf:

\[(({\color{red}x}_1,{\color{red}y}_1,{\color{red}z}_1), ({\color{darkred}v_x}_1,{\color{darkred}v_y}_1,{\color{darkred}v_z}_1), ..., ({\color{red}x}_n,{\color{red}y}_n,{\color{red}z}_n), ({\color{darkred}v_x}_n,{\color{darkred}v_y}_n,{\color{darkred}v_z}_n)) \in \mathbb{R}^{2\cdot 3\cdot n} = \mathbb{R}^{6 n}\]

Auch dies schreiben wir wieder kürzer als:

\[\left(({\mathbf{\color{red}x}}_1, \dot{\mathbf{\color{red}x}}_1), ..., ({\mathbf{\color{red}x}}_n, \dot{\mathbf{\color{red}x}}_n)\right) \in \mathbb{R}^{3n}\]

Wobei wir uns aussuchen können, ob wir \({\mathbf{\color{red}v}}\) oder \(\dot{\mathbf{\color{red}x}}\) schreiben möchten.

Wir können es auch ganz abstrakt auffassen, und den ganzen Systemzustand als einen einzigen Vektor \(\color{red}{\mathbf{X}}\) auffassen (wir schreiben den hier mal in Großbuchstaben). Damit bekommt man eine ganz einfache Formulierung für ein Differentialgleichungssystem:

\[\frac{d}{d{\color{darkblue}{t}}}{\color{red}{\mathbf{X}}}({\color{darkblue}{t}}) = {\mathbf{\color{red}f}}\Big({\color{red}{\mathbf{X}}}({\color{darkblue}{t}}), {\color{darkblue}{t}}\Big)\]

Hierbei werden wieder alle Ableitungen komponentenweise angewandt. Ausgeschrieben ergibt das:

\[%\frac{d}{d{\color{darkblue}{t}}}{\color{red}{\mathbf{X}}}({\color{darkblue}{t}}) = \left[ \begin{matrix} \frac{d}{d{\color{darkblue}{t}}} {\color{red}x}_1({\color{darkblue}{t}})\\ \vdots \\ \frac{d}{d{\color{darkblue}{t}}} {\color{red}x}_n({\color{darkblue}{t}}) \end{matrix} \right] %= {\mathbf{\color{red}f}}\Big({\color{red}{\mathbf{X}}}({\color{darkblue}{t}}), {\color{darkblue}{t}}\Big) = \left[\begin{matrix} {\color{red}f}_1\big({\color{red}x}_1({\color{darkblue}{t}}),...,{\color{red}x}_n({\color{darkblue}{t}}), {\color{darkblue}{t}}\big)\\ \vdots \\ {\color{red}f}_n\big({\color{red}x}_1({\color{darkblue}{t}}),...,{\color{red}x}_n({\color{darkblue}{t}}), {\color{darkblue}{t}}\big) \end{matrix} \right] \] Beispiel: Als Beispiel schauen wir uns mal die Gleichungen an, die die Rotation von Erde und Sonne umeinander (Hauptsächlich erstere um letztere) beschreiben. Hier schreiben wir die Positionen und Geschwindigkeiten wieder als 3D-Vektoren, sonst wird es zu unübersichtlich:

\[\frac{d}{d{\color{darkblue}{t}}} \left[ \begin{array}{c} {\mathbf{\color{red}x}}_{Erde}({\color{darkblue}{t}})\\[5pt] {\dot{\mathbf{\color{red}x}}}_{Erde}({\color{darkblue}{t}})\\[5pt] {\mathbf{\color{red}x}}_{Sonne}({\color{darkblue}{t}})\\[5pt] {\dot{\mathbf{\color{red}x}}}_{Sonne}({\color{darkblue}{t}}) \end{array} \right] = \left[\begin{array}{c} {\dot{\mathbf{\color{red}x}}}_{Erde}({\color{darkblue}{t}})\\ \gamma_0 \cdot \Big({\mathbf{\color{red}x}}_{Sonne}({\color{darkblue}{t}}) - {\mathbf{\color{red}x}}_{Erde}({\color{darkblue}{t}})\Big) \cdot \frac{m_{Sonne}}{\left\| {\mathbf{\color{red}x}}_{Sonne}({\color{darkblue}{t}}) - {\mathbf{\color{red}x}}_{Erde}({\color{darkblue}{t}}) \right\|^3}\\ {\dot{\mathbf{\color{red}x}}}_{Sonne}({\color{darkblue}{t}})\\ \gamma_0 \cdot \Big({\mathbf{\color{red}x}}_{Sonne}({\color{darkblue}{t}}) - {\mathbf{\color{red}x}}_{Erde}({\color{darkblue}{t}})\Big) \cdot \frac{m_{Erde}}{\left\| {\mathbf{\color{red}x}}_{Sonne}({\color{darkblue}{t}}) - {\mathbf{\color{red}x}}_{Erde}({\color{darkblue}{t}}) \right\|^3} \end{array} \right] \]

Die rechte Seite ergibt sich, indem wir das newtonsche Gravitationsgesetz anwenden, was auch für 3D Vektoren gilt (nicht nur für skalare Abstände). In der Formel oben steht dann die Länge des Abstandsvektors (Längen werden mit \(\| \cdot \|\) bezeichnet) in der dritten Potenz, um die Länge des Abstandsvektors, mit dem wir multiplizieren, wieder herauszukürzen (es bleibt also genau \(r^2\) übrig, wie zuvor). Danach haben wir \(a=F/m\) angewandt; dadurch kürzt sich für die Beschleunigung diejenige Masse des Himmelskörpers raus, der gerade beschleunigt wird.

Die numerische Lösung mit dem „expliziten Eulerverfahren“ funktioniert im Prinzip genauso wie zuvor: Wir aktualisieren die Geschwindigkeiten, indem wir die 3D Beschleunigungen ausrechnen und dies auf die Geschwindigkeiten aufaddieren (immer mit dem Zeitintervall \(\epsilon\) skaliert, um das wir fortschreiten wollen. Danach aktualisieren wir die Positionen, indem wir die Geschwindigkeiten aufaddieren.

Wenn man diese Gleichung lösen will, muss man initiale Positionen für Erde und Sonne, sowie initiale Bahngeschwindigkeiten für beide Himmelskörper festlegen. Vergisst man letzteres, stürzt die Erde in die Sonne und in der nähe der Singularität (kurz vor der Gleichheit der Werte) fliegt einem beim Eulerverfahren typischerweise die Erde aus dem Wertebereich (da die Kräfte so groß werden, dass die Position im nächsten Schritt extrem groß wird). Also merke: Beim Bauen von Sonnensystemen (kommt ja immer wieder mal vor), die Geschwindigkeiten nicht vergessen!

Nach dem gleichen Prinzip kann man beliebige Differentialgleichungen (auch mit höherem Grad und vielen Freiheitsgraden) in ein System von Gleichungen ersten Grades umwandeln und dann ein Anfangswertproblem numerisch Lösen.

Andere Kräfte

Zu guter Letzt sei noch erwähnt, dass man in Modellen der klassischen Mechanik noch weitere Wechselwirkungen zwischen Partikeln zur Verfügung stehen. Beliebt sind die folgenden:

Coulombsches Gesetz: Anziehung/Abstoßung elektrisch geladener Teilchen:
\[{\color{red}F}=\frac{1}{4i\epsilon_0} \cdot \frac{q_1 \cdot q_2}{{\color{red}r}^2}\]

Hier ist \(\epsilon_0\) die elektrische Feldkonstante und \(q_1\) und \(q_2\) sind die vorzeichenbehafteten Ladungen der Partikel. Aufpassen: gleiche Ladungen stoßen sich ab, verschiedene ziehen sich an. Man kann dieses Gesetz auch (wie in Formel (20) benutzt) in vektorieller Form schreiben. Der Kraftvektor wirkt zwischen den Ladungen und hat die Länge aus (21) und das Vorzeichen entsprechend der Ladungskombination. Elektrische Kräfte sind wesentlich stärker als Gravitation; allerdings treten gleiche Ladungen selten gemeinsame und ohne gegenteilig geladene Teilchen am selben Ort auf (sonst explodiert das Objekt halt sofort). Daher bemerkt man sie in der Praxis meist nicht direkt.

Hooksche Federn: Ein lineares Modell für Federn; wenn keine extremen Auslenkungen auftreten, ist dieses Modell ein sehr realistisches Abbild echter Federn (z.B. klassische Spiralfedern aus Stahl): \[{\color{red}F}= -D \cdot ({\color{red}r}-r_0)\]

Die Kraft nimmt hier linear mit der Federauslenkung zu (und wird entgegen der Auslenkung). \(D\) ist die Federkonstante (je höher desto stärker ist die Feder; es treten höhere Rückstellkräfte auf), und \({\color{red}r}\) bzw. \(r_0\) sind die Auslenkung und die entsprechende Ruhelänge der Feder. Vektoriell sieht die Gleichung wieder ganz ähnlich aus — die Kräfte wirken entsprechend in Richtung des Verbindungsvektors.

Reibung & Dämpfung: Zu guter Letzt treten in allen realistischen physikalische Systemen auch Reibungskräfte auf, die nach und nach die Bewegung des Systems dämpfen und es zum Stillstand bringen (was bleibt, sind die thermischen Bewegungen der Elementarteilchen, aber das modellieren wir in einem klassischen Newtonschen Modell nicht explizit). Typischerweise wird dies formal so modelliert, dass man eine Kraft definiert, die der Bewegungsgeschwindigkeit entgegenwirkt. Für einfache Reibung (auf Oberflächen, oder in Achsen), nimmt man in der Regel an, dass die Reibungskraft proportional zur Geschwindigkeit ansteigt:
\[{\color{red}F}= -c \cdot {\color{red}v}({\color{darkblue}{t}})\] Für Luftwiderstand (oder auch unter Wasser), beobachtet man eher einen quadratischen Anstieg der Reibungskräfte:
\[{\color{red}F}= -c \cdot {\color{red}v}({\color{darkblue}{t}})^2\] Der Koeffizient \(c\) gibt jeweils an, wie stark die Reibung ist.
Diese Formulierung hat gewisse numerische Risiken: Bei sehr stark gedämpften Systemen (der Fachbegriff in der Numerik ist „steife Differentialgleichungen“) treten sofort sehr große Gegenkräfte auf. Dies bedeutet, dass man in sehr kleinen Schrittweiten lösen muss; sonst kann es sein, das der Schritt in die Gegenrichtung stärker als die ursprüngliche Bewegung ausfällt und die approximative Lösung sich aufschaukelt; die Lösung „explodiert“ innerhalb weniger Schritte (siehe nächster Abschnitt). Ein beliebter Trick ist daher, einfach in jeden Zeitschritt einen Bruchteil der Geschwindigkeit zu nehmen, also z.B. \(v(t+h) = 0.99 \cdot v(t)\). Für einfache Anwendungen, wie in unseren Aufgaben, ist so eine Form von Dämpfung ausreichend und vermeidet Stabilitätsprobleme. Bei Simulationen von „echten“ physikalischen Systemen, muss man hier mehr Arbeit aufwenden, um Stabilität zu erhalten (z.B. durch bestimmte Varianten von sogenannten „implizite“ Lösungsverfahren).

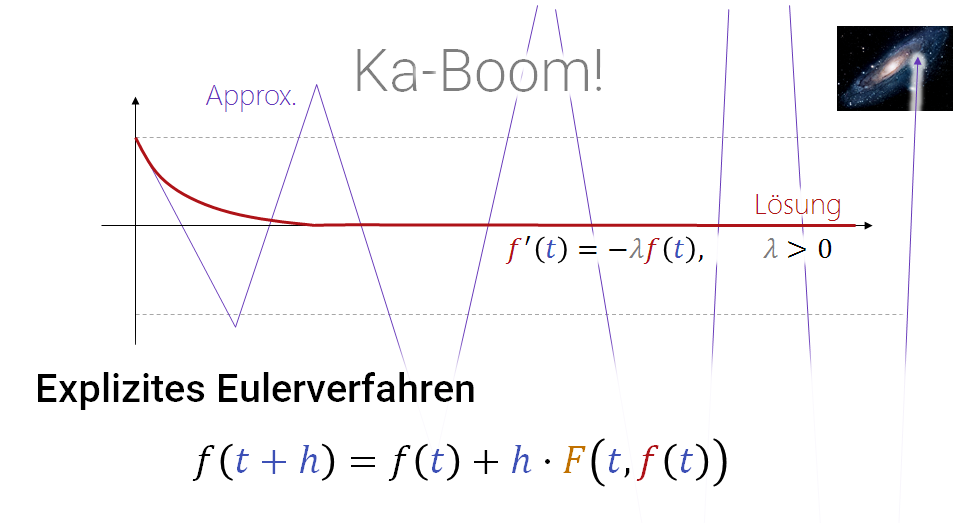
Numerische Stabilität: Bei sehr steifen Federn oder bei starker Reibung muss man bei der numerischen Lösung besonders aufpassen. Grundsätzlich liefern Näherungsverfahren, wie das hier besprochene explizite Eulerverfahren, nur ungefähre Lösungen, die von der richtigen Lösung noch abweichen. Bei Systemen, die sehr stark auf kleine Zustandsänderungen reagieren (z.B. starke Federn oder starke Dämpfungskräfte), können die Näherungsfehler sich „katastrophal“ aufschütteln, wenn man nicht in sehr kleinen Schrittweiten simuliert. Das hier in diesem Dokument diskutierte „explizite Eulerverfahren“ ist für solche Probleme anfällig: Wenn die Rückstellbeschleunigung (Feder oder auch Dämpfung) z.B. um einen Faktor 1000 pro Zeiteinheit steigt, darf man höchstens einen Schritt um \(h \ll 2/1000\) machen. Überschreitet man diese Schranke, so würde die verwendete linearen Extrapolation eine rückwärtsgewandte Geschwindigkeit erzeugen, die im Betrag um einen Faktor größer ist als die zuvor herrschende (mit umgekehrtem Vorzeichen). Dieser Prozess setzt sich dann exponentiell fort, und die Fehler „schaukeln“ sich exponentiell auf (umgangssprachlich auch bekannt als „Ka-Bumm“: nach kürzester Zeit bekommt man einen Fließkommaüberlauf). Diese Probleme kann man vermeiden, indem man eine unbeschränkte Extrapolation verhindert. Dies geschieht bei vielen der sogenannten „impliziten“ Lösungsverfahren. Für unsere Veranstaltung gehen diese Feinheiten zu weit — hier nur der Hinweis, dass man bei den Schrittweiten aufpassen muss, und das hohe Rückstell- oder Dämpfungskräfte numerisch „gefährlich“ sind.

„Solid & Fluid Dynamics“ — Simulation von ausgedehnten, elastischen Objekten und/oder Flüssigkeiten

Das hier vorgestellte Partikelmodell beschreibt nur eine recht einfache Klasse von Modellen. Elastische Festkörper sind nur schwer damit zu realisieren; Flüssigkeiten machen noch mehr Probleme. Ein beliebter Trick, um nicht-punktförmige, elastische Objekte zu modellieren, besteht darin, diese in viele Partikel zu zerlegen, die man dann mit relativ steifen Feder verbindet. Leider funktioniert das in der Praxis nicht sehr gut — zum einen hat dieses Modell „Anisotropieartefakte“ (die Richtungen der Feder merkt man der Simulation an; man bekommt auch bei feiner Aufteilung kein wirklich realistisches Ergebnis). Bei Flüssigkeiten müsste man komplexere Anziehungs- und Abstoßungskräfte modellieren. In der Regel weicht man in beiden Fällen auf andere Modelle aus, die mit partiellen Differentialgleichungen arbeiten, die ein Kontinuum von Materie (Wasser, Festkörper, Mischungen davon) beschreiben, ohne eine explizite Zerlegung in atomare Partikel. Auch dies geht erst einmal über den Rahmen unserer Veranstaltung hinaus (mehr dazu später im Studium in vertiefenden Veranstaltungen der Mathematik oder der Computergraphik / mathematischen Modellierung in der Informatik).