
Institut für Informatik
Michael WAND
Christian ALI MEHMETI-GÖPEL
Sommersemester 2024

|
Institut für Informatik
Michael WAND Sommersemester 2024 |
Michael Wand, Institut für Informatik,
23. August 2020
(aktualisiert: 06. Oktober 2021)

Eine (noch unvollständige) Wiederholung der Konzepte der Vorlesung Modellierung 1
Dieses Dokument fasst einige der Themen der Vorlesung Modellierung 1 nochmal in Textform zusammen. Es erhebt nicht den Anspruch auf Vollständigkeit. Zum einen sind einige Teile und Kapitel noch nicht zu Ende geschrieben, zum anderen wurden auch Aspekte bewußt ausgelassen (z.B. um eine gradlinigere Erklärung liefern zu können, oder auch weil die Ideen in den Folien besser erklärt werden konnten). Das Dokument soll bei der Prüfungsvorbereitung helfen, ersetzt aber nicht die Vorlesung selbst. Insbesondere können in Prüfungen auch Fragen über den Stoff dieser Zusammenfassung hinaus gestellt werden.
Das Ziel dieses Aufschrieb ist auch, für die ersten Kapitel der Vorlesung die formalen Hintergründe etwas genauer zu sammeln und als Nachschlagewerk zur Verfügung zu stellen. Aus Komplexitätsgründen konnte wird hier aber auch auf Literaturquellen für viele der Details verwiesen. Stichwort Literatur: Viele Links führen zu Wikipedia, da dort viele Konzepte sehr schön aufbereitet sind. Man sollte Webquellen (und insbesondere solche, die von der Allgemeinheit frei bearbeitet werden können), aber immer aufmerksam lesen, da sich vielleicht noch hier und da ein Fehler eingeschlichen haben könnte. Das gilt leider auch für diesen Aufschrieb - der Text ist keinem formalen Review unterzogen worden und kann daher auch durchaus noch den ein oder anderen kleinen (oder größeren) Fehler enthalten.
Übungsaufgaben
Im Dokument sind immer wieder Übungsaufgaben zur Vertiefung des Stoffes eingebaut (immer am Ende des Kapitels). Diese sind rot markiert, damit man sie leicht findet, falls man vor allem an den Aufgaben interessiert ist.
Noch ein Wort zum Konzept: Ziel der Vorlesung wie auch dieses Aufschriebs ist eine informelle, übersichtsartige Einführung in die Modellierung, die “gut genug” sein sollte, um Probleme im Visual Computing (Graphik, Computer Vision) lösen zu können. Es besteht aber kein hoher Anspruch an mathematische Strenge und Präzision. Wenn Sie dies richtig lernen wollen, müssen Sie eine Vorlesung in Mathematik oder (theoretischer) Physik besuchen. Bevor Sie eine FEM-Simulation zur Bruchfestigkeit einer Konstruktion für ein Verkehrsflugzeug durchführen: Besuchen Sie unbedingt eine professionellere Vorlesung zu diesen Themen! Die Techniken hier sind auf einem Niveau dargestellt, das eher für Computerspiele als für Anwendungen mit ernsten Konsequenzen gedacht ist.
Ich hoffe natürlich, dass man trotzdem etwas lernt, und weil alles nicht in die letzten Details sauber durchexerziert wird, schneller einen guten Überblick über die Konzepte und Zusammenhänge erhält.
Nun viel Spaßt beim Lesen.
tl;dr – Hoch-dimensionale Vektoren sind der Schlüssel
Die Vorlesung Modellierung 1 beschäftigt sich mit der Techniken für die Modellierung “natürlicher” oder “realer” Phänomene. Dabei nimmt man an (und die Erfahrung gibt uns recht - es scheint tatsächlich zu funktionieren), dass man die Dinge der Welt in (halbwegs) einfache und kompakte mathematische Formeln fassen kann. Um dies zu tun, brauchen wir zwei Dinge:
Es gibt durchaus abgefahrene Repräsentationen, mit denen man theoretisch arbeiten kann. Ein unkonventionelles Beispiel wären geometrische Grammatiken (Shape Grammars), die in der Computergraphik für die Modellierung von Architektur eingesetzt werden. In den allermeisten Fällen verwendet man in der modernen Wissenschaft jedoch lineare Repräsentationen. Dabei wird das Modell durch einen Vektor in einem Vektorraum repräsentiert, welcher in der Praxis schlicht durch eine Liste von Zahlen repräsentiert wird.
Von der Wettersimulation, über Crash-Tests bis hin zur Quantenmechanik - überall wird der Systemzustand als Vektor in einem linearen Raum repräsentiert. Durch Änderung der Koordinaten kann man dann verschiedene Zustände auswählen, bis derjenige gefunden ist, der nach den Regeln das System richtig beschreibt.
Entsprechend schauen wir uns in dieser Vorlesung nur lineare Repräsentationen an.
Abstrakt gesprochen sind die Regeln mathematische Gleichungen, die (bei einem linearen Modell) die Wahl des richtigen Vektors aus der Menge aller möglichen Vektoren bewirken sollen. Dazu gehören Fall-spezifische Randbedingungen wie auch allgemeine Regeln. Oft spricht man von Modellierung, wenn man die Repräsentation und die allgemeingültigen Regeln aufstellt, und von Simulation oder Lösung des Modells, wenn man für spezielle Randbedingungen durchrechnet, welche Modellparameter alles erfüllen.
Ok. Was nun? Wir müssen als erstes verstehen, wie man (allgemein) Vektoren formulieren kann. Dabei ist die lineare algebraische Struktur der Schlüssel, mit dem man effiziente Algorithmen zur Lösung (Simulation) finden kann. Daher müssen wir uns genauer anschauen, was das heißt.
Vektoren sind ein mathematisches Konzept, mit dem man geometrische Objekte in mehrdimensionalen (flachen, im Sinn von nicht intrinisch gekrümmten; man nennt dies auch “Euklidische Geometrie”) Räume beschreiben kann.
Die Idee kennen wir aus der Schule. Vektoren sind Pfeile, die man aneinanderhängen (addieren) und skalieren (Multiplikation mit Zahlen) kann:

Außerdem kennen wir aus der Schule auch noch das Skalarprodukt, mit dem man Längen und Winkel messen kann:
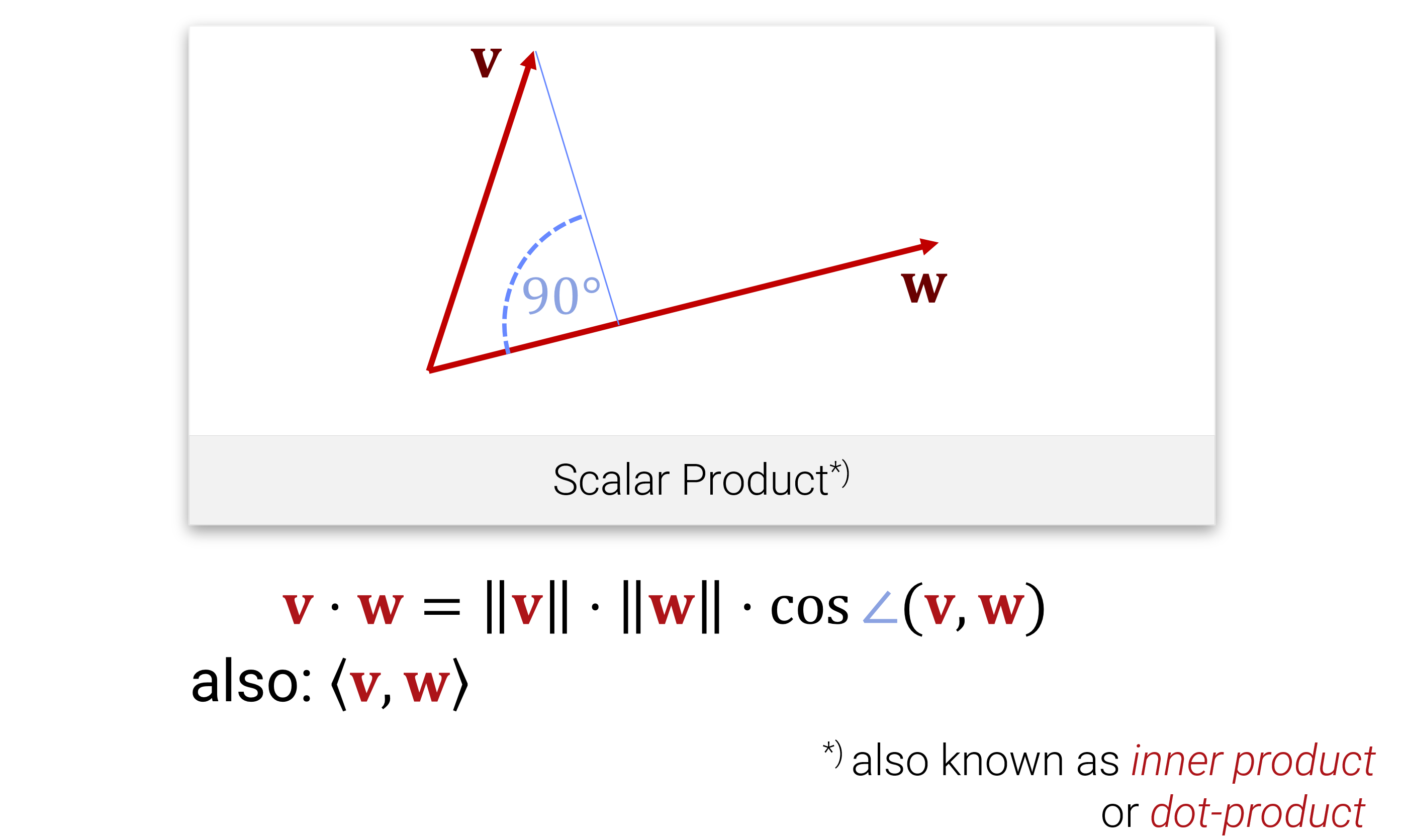
Entsprechend definiert man die Länge eines Vektors als \[||\mathbf{x}|| := \sqrt{\langle \mathbf{x} , \mathbf{x} \rangle }\] und den Winkel zwischen zwei Vektoren als \[\angle (\mathbf{x}, \mathbf{y}) := \operatorname{cos}^{-1}\Big \langle \frac{\mathbf{x}, \mathbf{y}}{||\mathbf{x}|| \cdot ||\mathbf{y}||} \Big \rangle.\]
Wenn der Winkel \(90^\circ\) ist, also \(\langle \mathbf{x}, \mathbf{y} \rangle = 0\), dann nennt man die Vektoren orthogonal.
Die geometrische Formel kann man übrigens auch so interpretieren, dass \(\langle \mathbf{x}, \mathbf{y} \rangle\) eine Projektion des einen Vektors auf den anderen ist. Falls wir annehmen, dass einer der beiden normiert ist, also die Länge 1 hat, dann misst man, wie weit der andere in die richtung des normierten zeigt. Sagen wir obdA. dass der zweite normiert ist, \(||\mathbf{y}||=1\), dann erhält mal das \(\langle \mathbf{x}, \mathbf{y} \rangle = ||y|| \cdot \cos \angle \mathbf{x}, \mathbf{y}\). Man fällt also das senkrechte Lot vom Ende des Pfeiles \(\mathbf{x}\) herunter auf die gerade durch \(\mathbf{y}\) und das Skalarprodukt liefert genau die Länge des Abschnitts in die Richtung von \(\mathbf{y}\) (mit Vorzeichen):
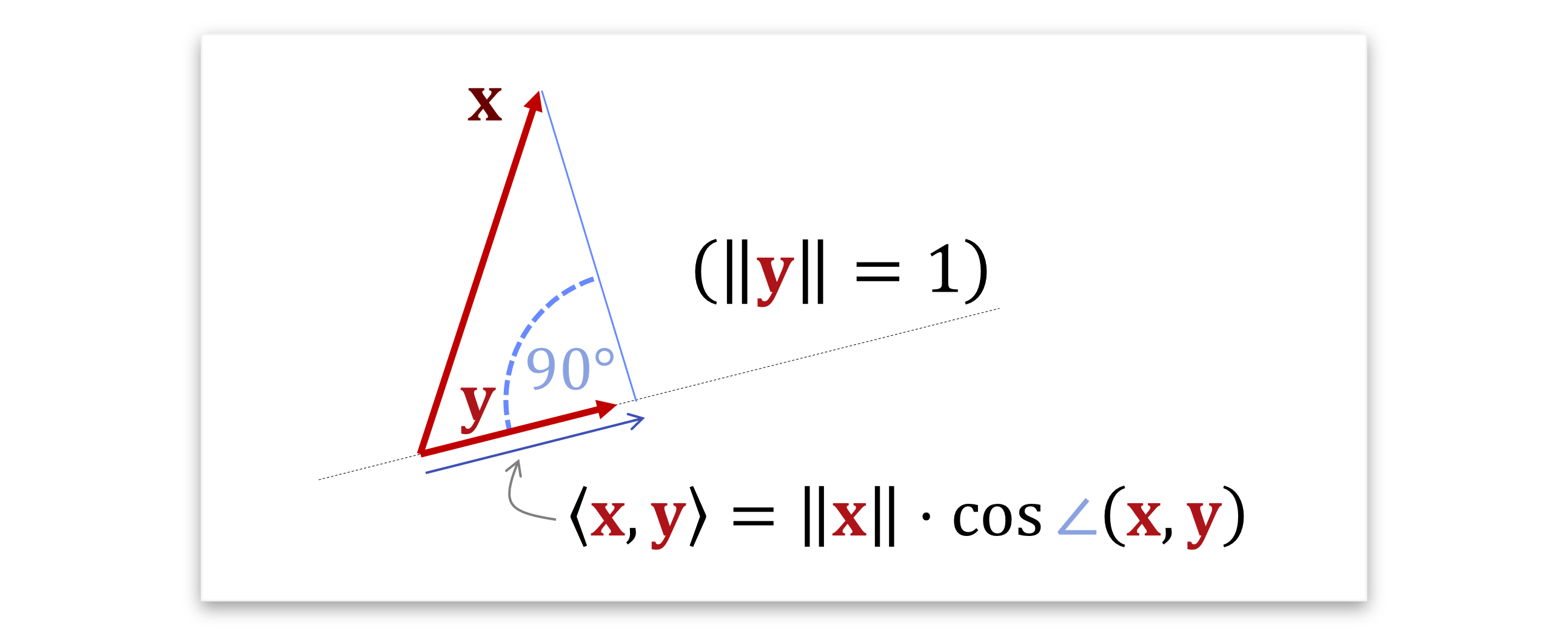
Notation: Damit wir nicht durcheinanderkommen, schreiben wir geometrische Vektoren (z.B. \(\mathbf{x} \in \mathbb{R}^d\)) fett, und Zahlen normal-kursiv (z.B. \(a \in \mathbb{R}\)). Matrizen werden wir später auch fett notieren (z.B. \(\mathbf{M} \in \mathbb{R}^{m\times n}\)). Außerdem nehmen wir hier immer an, das Vektoren als Spalten geschrieben werden (und später entsprechend von rechts mit Matrizen multipliziert werden müssen). Die einzelnen Einträge in einem Vektor \(\mathbf{x} \in \mathbb{R}^d\) bezeichnen wir als \(x_1,...,x_d \in \mathbb{R}\). Das gleiche machen wir für Matrizen: \[ \mathbf{M} \in \mathbb{R}^{n \times k}, \ \ \ \mathbf{M} = \left( \begin{array}{rrr} m_{1,1} & \cdots & m_{n,1} \\ \vdots & \ddots & \vdots \\ m_{1,k} & \cdots & m_{n,k} \end{array} \right) \]
PS: Es ist durchaus üblich, die Koordinaten der Matrix andersherum (Zeile, Spalte) zu schreiben. Mir gefällt die hier benutzte “(x,y)”-Konvention besser; aber das ist Geschmackssache.
Wenn man im Rechner mit solchen Vektoren rechnen will, dann repräsentiert man die Pfeile mit ihren (x-,y-,z- etc.) Achsenabschnitten und speichert sie als Liste von Zahlen. Im \(d\)-dimensionalen Raum nutzt man also Arrays aus \(\mathbb{R}^d\). Die Addition und Multiplikation mit einer Zahl werden dann komponentenweise durchgeführt (was ziemlich offensichtlich das richtige macht), und für das Skalarprodukt muss man die Komponenten einzeln zusammenmultiplizieren und aufaddieren (man kann beweisen, dass dies alles der geometrischen Intuition entspricht).
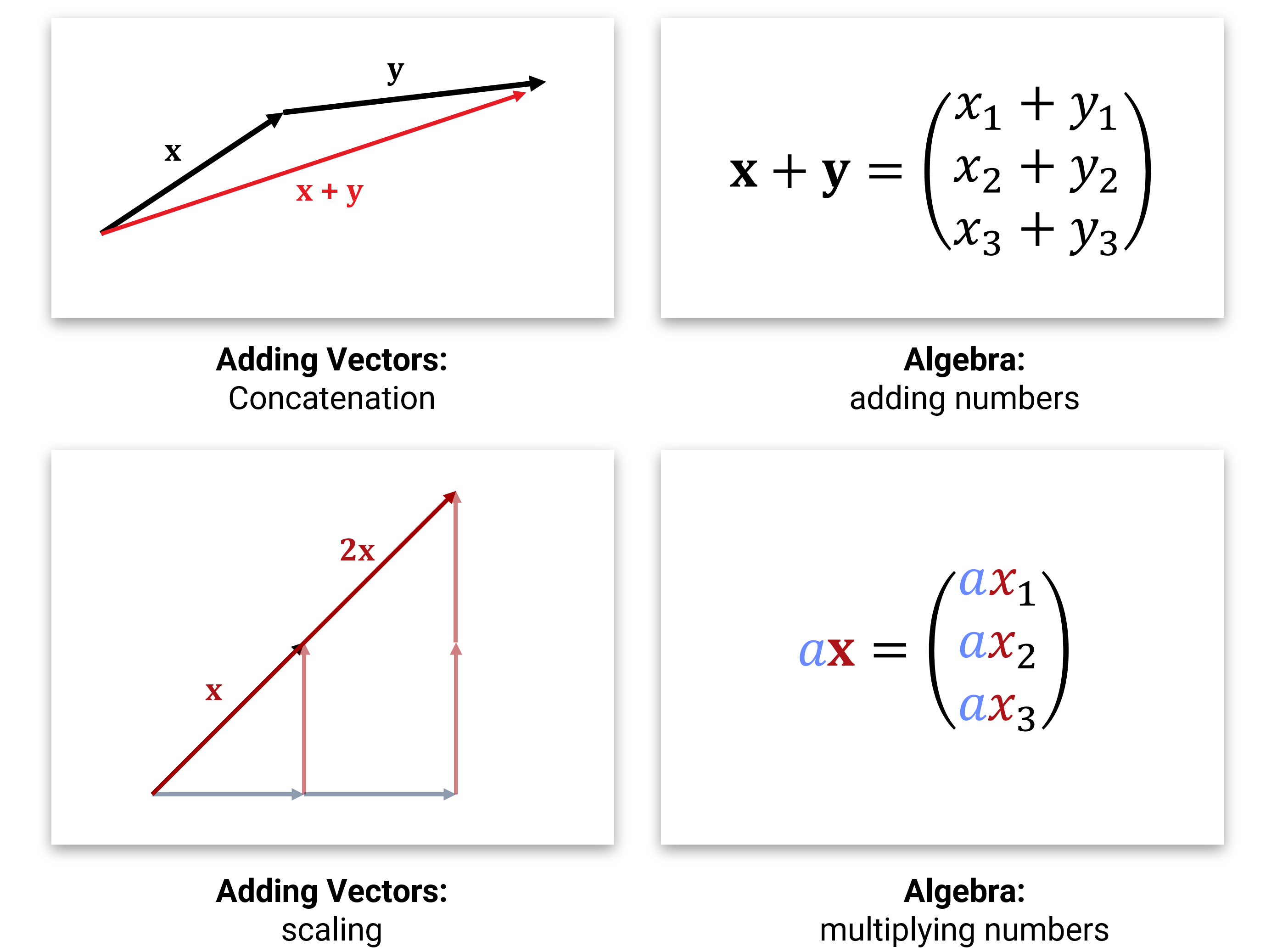
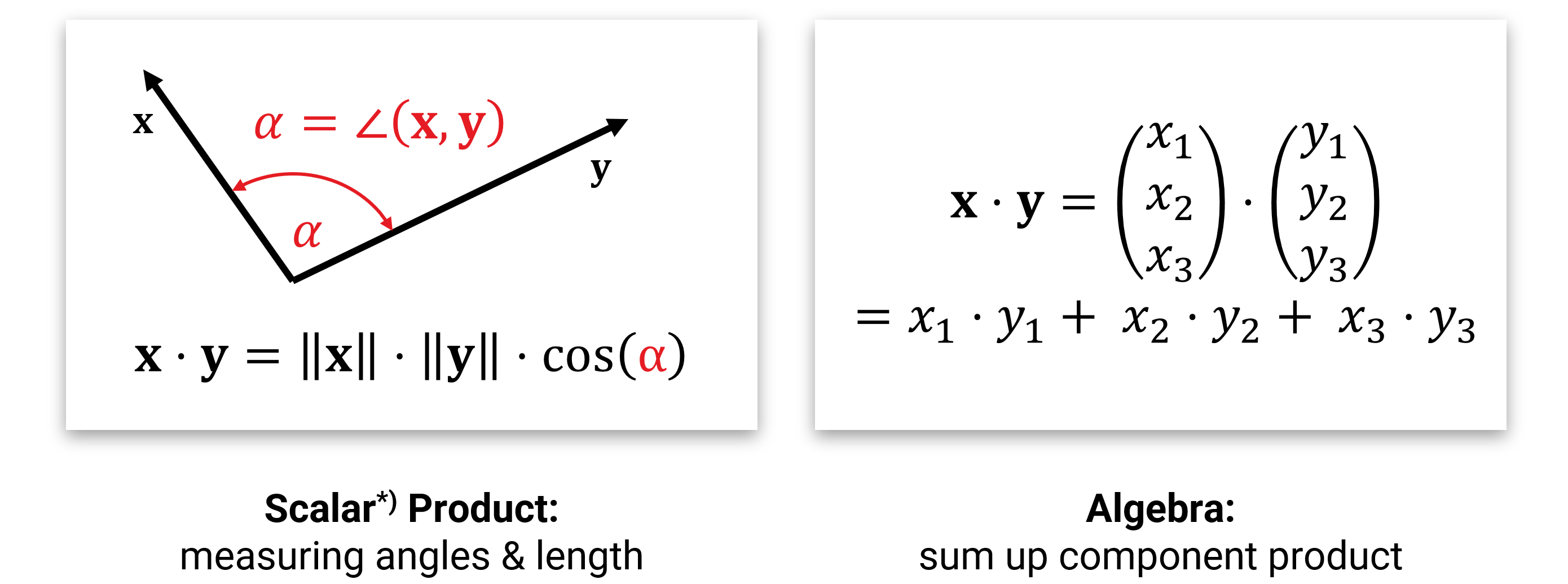
Mit diesen Werkzeugen kann man nun z.B. geometrische Objekte (typischerweise im zwei- oder dreidimensionalen Raum) darstellen. Hier eine kurze Übersicht, wie man das anstellen kann:
Punkte: Wir benutzen “Ortsvektoren”, d.h., wir merken uns die Abstand des zu beschreibenen Punkt vom Ursprung.
Geraden: Wir betrachten die Menge aller \[\mathbf{x}(t)= \mathbf{m} \cdot t + \mathbf{n}\] für alle \(t \in \mathbb{R}\) und für feste \(\mathbf{m}, \mathbf{n} \in \mathbb{R}^d\). Wenn wir \(t\) variieren, laufen wir entlang der Gerade. Wir können Geraden auch implizit beschreiben, als die Menge aller \(\mathbf{x} \in \mathbb{R}^d\), die die Gleichung \[\langle \mathbf{m} , \mathbf{x} \rangle + \mathbf{n} = 0\] löst.
(Hyper-) Ebenen: Nun bauen wir eine \(k\)-dimensionale Hyperebene im \(\mathbf{R}^d, 0 \le k \le d\). Sehr oft ist \(k=2\) und \(d=3\), d.h., wir interessieren uns für eine ganz profane Ebene im 3D Raum. Wir beschreiben wir soetwas mathematisch? Wir betrachten die Menge aller \[\mathbf{x}(t_1,...,t_k) = \sum_{i=1}^k \mathbf{m_i} \cdot t_i + \mathbf{n}\] für alle \(\mathbf{t} \in \mathbb{R}^k\) und für feste \(\mathbf{m}, \mathbf{n} \in \mathbb{R}^d\). Wenn wir \(t\) variieren, laufen wir entlang der Gerade.
Wenn \(k=d-1\) (und leider nur dann), dann können wir auch die (selbe!) implizit Form benutzen, wie für die Gerade (das wäre genau der Fall \(d=2, k=1\)). Also, wir stellen uns alle \(\mathbf{x} \in \mathbb{R}^d\) vor, für die \(\langle \mathbf{m} , \mathbf{x} \rangle + \mathbf{n} = 0\) ist.
Dreiecke: Ein Dreieck kann mit drei Punkten kodiert werden. Die Fläche selbst können wir auch explizit als
\[\mathbf{x}(t_1,t_2) = \mathbf{m_1} \cdot t_1 + \mathbf{m_2} \cdot t_2 + \mathbf{n} \\ \text{ mit } t_1 \ge 0, t_2 \ge 0 \text{ und } t_1 + t_2 \le 1\]
darstellen (wir dürfen auf der Ebene also nur innerhalb des Dreiecks laufen). Implizite Dreiecke sind leider sportlich (viel Glück).
Teekannen und Tonhasen: Komplexere geometrische Objekte kann man durch Dreiecke (für 2D oder, analog, Liniensegmente für 1D, Tetraeder für 3D oder ähnliches) approximativ zusammenbauen. Man nennt das ganze ein Dreicksnetz (bzw. “Simplizialkomplex” in allgemeinen Dimensionen). Hier ein Beispiel von einem berühmten Tonhasen:

Parametrische Kurven und Flächen: Man kann auch glatte Objekte modellieren, indem man eine nichtlineare Funktion von einen oder mehreren Paramtern bildet. Eine Funktion mit einem Parameter \[ f: \mathbb{R} \rightarrow \mathbb{R}^d \] nennt man eine parametrische Kurve, und eine Funktion von zwei Variablen \[ f: \mathbb{R}^2 \rightarrow \mathbb{R}^d \] nennt man eine parametrische Fläche. Man kann natürlich auch noch mehr Eingaben machen; das ganze ergibt dann höherdimensionale Objekte (eingebettet in einem noch höher-dimensionalen Raum). In der Vorlesung hatten wir ein paar Beispiele dafür; hier nochmal eine Übersichtsgraphik mit solchen Beispielen:
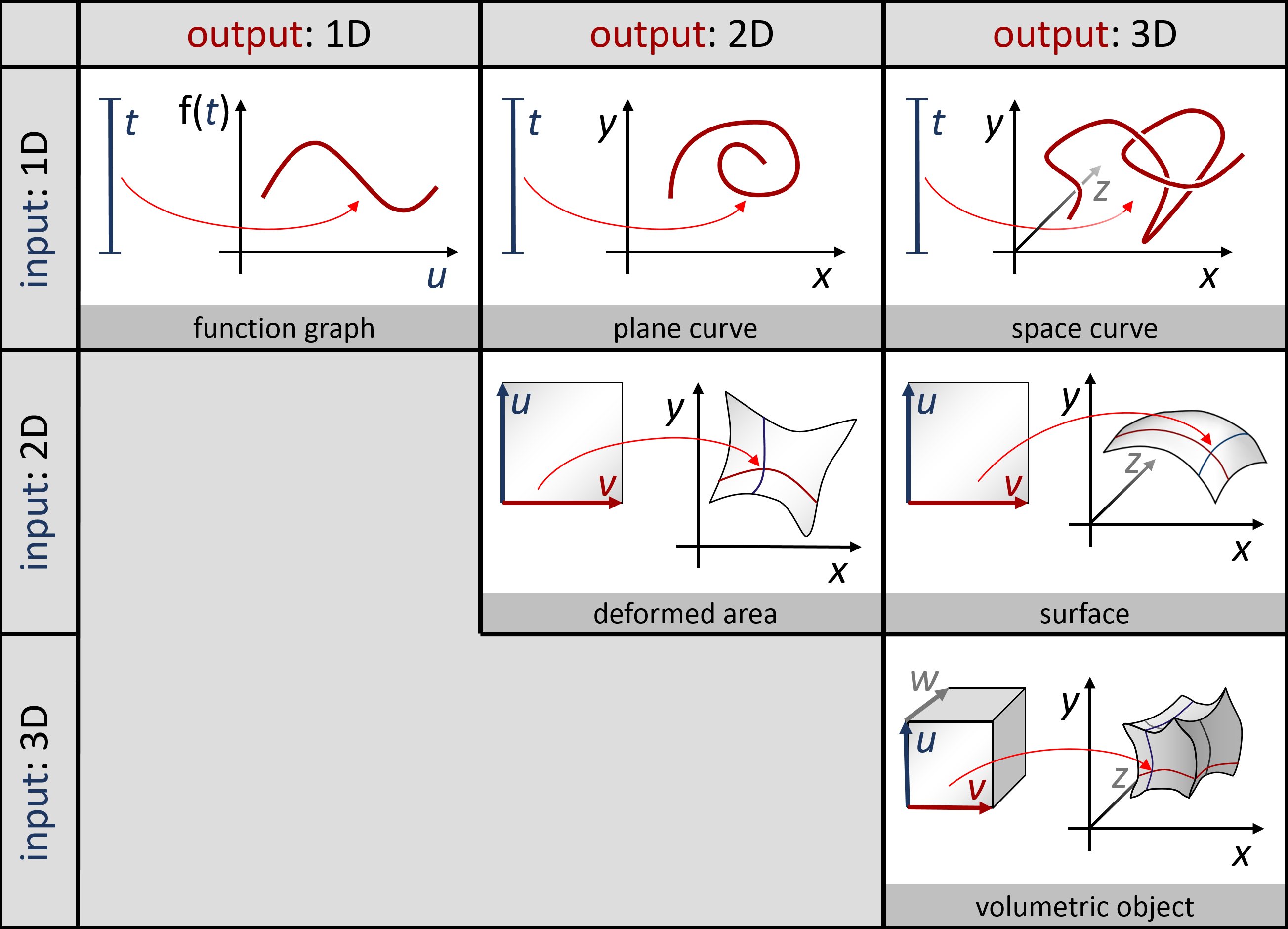
In praktischen Anwendungen werden gerne Splines (stückweise polynomielle Funktionen) benutzt, um schön glatte Kurven und Flächen zusammenzubasteln.
So, jetzt beherrschen wir die Geometrie - was kann man damit machen? Die Kernidee ist, dass man sich komplexere Modelle als geometrische Objekte in (hinreichend) hoch-dimensionalen Räumen vorstellt. Zum Beispiel könnte man die Verformung eines virtuellen Autos in einer Crash-Test-Simulation als Punkt in einem hochdimensionalen Raum vorstellen. Der gesamte Simulationslauf, der das Auto ordentlich verbiegt, wäre dann eine Kurve in diesem Raum. Die Kurve selbst (also die gesamte Entwicklung über die Zeit) könnte man dann, wenn man möchte, wieder zu einem Punkt in einem noch höher-dimensionalen Raum zusammenfassen.
Was hätten also alle diese Modelle gemeinsam? Als Informatiker*innen sind wir natürlich immer an generischen Algorithmen interessiert, die polymorph mit verschiedenen Daten gleichartig arbeiten können. Damit das klappt, sammeln wir nun die Axiome (aus dem Mathebuch) zusammen, die alle die oben genannten Formulierungen von “Punkten in einem Raum der so ähnlich wie 2D/3D arbeitet” zusammenfassen. Für den \(d\)-dimensionalen Raum \(\mathbb{R}^d\) wären wir ja schon fertig; es gibt aber interessante Fälle, die darüber hinausgehen (im Wesentlichen sind das Funktionenräume, siehe Abschnitt 1.4; die anderen Verallgemeinerungen sind für unser Anwendungsgebiet der Simulation natürlicher Phänomene weniger wichtig).
Vektorräume: Die freundlichen Kolleg*innen aus der Mathematik haben sich einige Jahrhunderte lang über dieses Problem den Kopf zerbrochen, und die aktuelle Abstraktion der Wahl ist die eines “(linearen) Vektorraums (Vector Space)”, und wenn wir alle o.g. Features möchten, mit dem Zusatz “mit Skalarprodukt”.
Die genauen Definitionen, Eigenschafte und Beweise kann man in unzähligen Mathematikbüchern nachlesen; für kurzentschlossene hat auch hier Wikipedia eine Zusammenfassung. Gleiches gilt für das Skalarprodukt, das man als Feature nachrüsten kann.
Hier sind nochmal kurz die Axiome aus der Vorlesung:
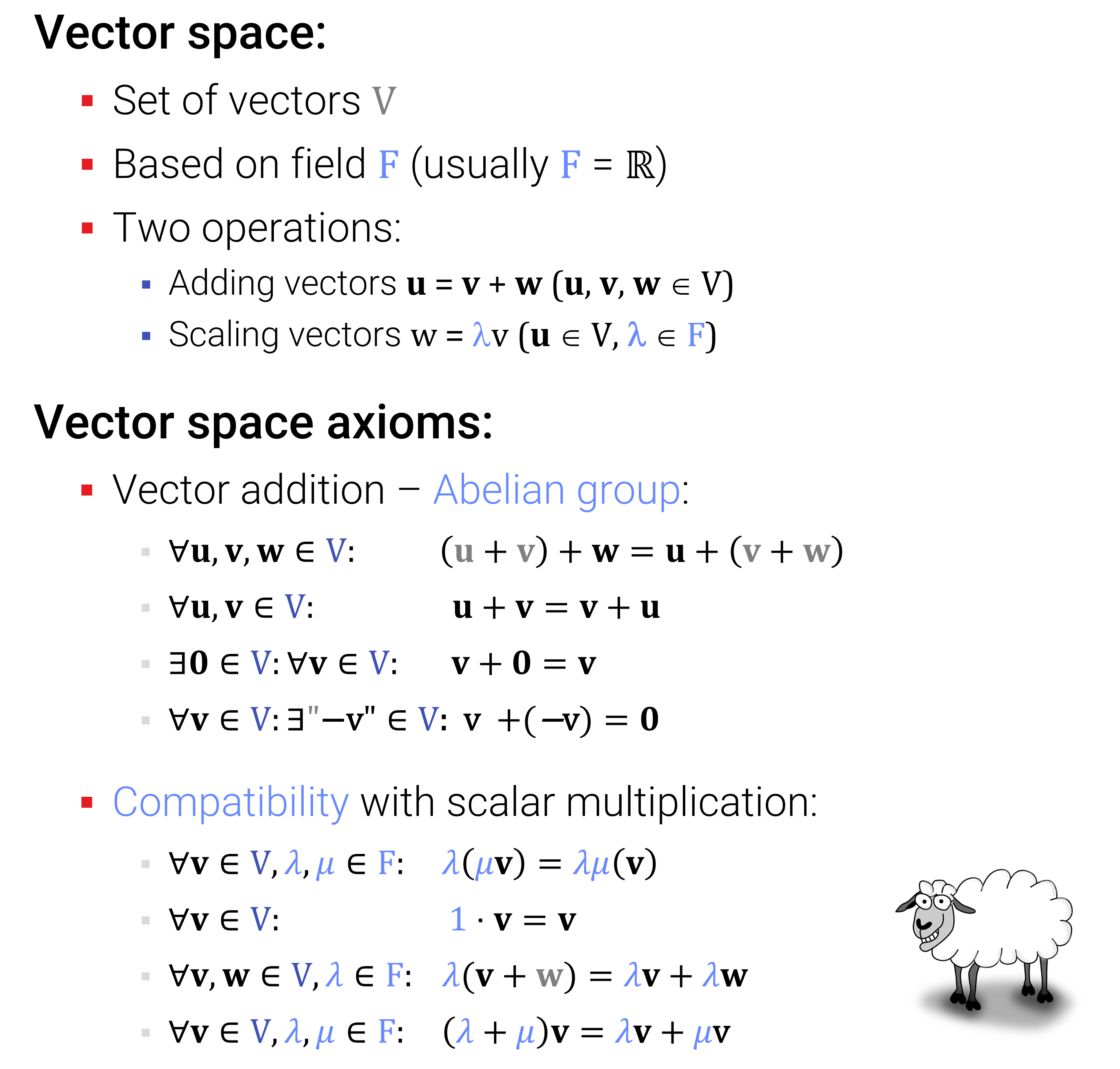

Grob zusammengefasst: Man möchte alle bekannten Rechenregeln für die zuvor definierten geometrischen Vektoren im \(\mathbb{R}^d\) erhalten. Allerdings erlaubt man nun als Zahlen beliebige Körper und als Vektoren abstrakte Objekte, die nicht unbedingt Listen von Zahlen sein müssen. Wie wir im nächsten Unterabschnitt sehen werden, ist das allerdings gar kein so großer Unterschied – am Ende reichen doch die Listen von Zahlen.
Zahlen? In unserer Vorlesung werden wir fast immer nur Zahlen aus \(\mathbb{R}\) nutzen, mit einer kleinen Ausnahme: Beim Kapitel über die Fourier-Theorie arbeiten wir mit komplexen Vektorräumen (Funktionenräumen), in denen als Zahlen komplexe Zahlen erlaubt sind. An dieser Stelle benutzen wir auch die übliche Modifikation eines “hermitschen” (komplexen) Vektorraumes, in dem das “Symmetrie”-Axiom leicht verändert wird zu \[ \langle \mathbf{x} , \mathbf{y} \rangle = \overline{\langle \mathbf{y} , \mathbf{x} \rangle}, \] wobei der Strich über dem Ausdruck für die komplexe Konjugation steht.
Andere Typen von Körpern, wie Restklassenkörper \(\mathbb{F}_k\) sind eher etwas für Kryptologen – wir benutzen das hier nicht.
Man kann mit Vektorräumen – grob gesagt – genauso rechnen (und algebraische Umformungen machen), wie wir es von normalen Zahlen kennen. Man muss nur beachten, dass es keine Multiplikation von Vektoren mit Vektoren im selben Sinne wie bei Zahlen gibt (das Skalarprodukt liefert ja keinen Vektor zurück, sondern eine Zahl); entsprechend gibt es auch keine Division durch Vektoren.
Die gerade genannte Daumenregel ist natürlich mathematisch nicht besonders präzise; um es genau zu wissen, muss man nochmal die Rechenregeln aufzählen, die sich aus den Axiomen herleiten lassen. Für dieses Dokument ist das zu viel – schauen Sie hier nochmal in ein Mathematikbuch (online z.B. Wikibooks Mathe für Nicht-Freaks: Lineare Algebra).
Wir beschränken uns hier auf die wichtigsten Begriffe und Sätze, die ich im folgenden nochmal kurz aufzähle:
Begriffe
Sätze (exemplarisch, ohne Beweis)
Beweis zum Basisisomorphiesatz: (passt im Prinzip auf einen Bierdeckel)
Jeder Vektorraum hat eine Basis. Aus der Basis kann man jeden Vektor linearkombinieren, mit Faktoren aus \(F\). Wenn die Basis endlich ist, reichen genau \(d=\operatorname{dim}(V)\) solche Zahlen. Mit denen kann man dann statt mit den Originalvektoren rechnen. Das das ein bijektiver Homomorphismus ist, ist “offensichtlich” (formal: doch noch einiges an Fleißarbeit, alles nochmal zu checken).
Was soll das ganze?
Greifen wir den letzten Satz nochmal auf: Wir wollten ja eigentlich von den Listen von Zahlen (\(\mathbb{R}^d\)) weg, die wir seit Zeiten kurz nach Decard’s kartesischen Koordinaten schon beherrschen. Nun haben wir alles axiomatisiert, und bewiesen, das die Axiome nichts anderes als \(F^d\) darstellen können? Und als Körper benutzen wir eh nur \(F=\mathbb{R}\)? (Der Frust steigt dadurch, wie offensichtlich das ist \(\rightarrow\) Bierdeckel!)
Also war das ganze wohl nur eine Übung intellektueller Gymnastik. Oder? Ach ja, da waren noch die unendlich-dimesionalen Vektorräume, bei denen das nicht so einfach geht – entgeht und da etwas? Wahrscheinlich nicht, schließlich paßt nichts unendliches in unseren Rechner. Aber einen Blick ist es trotzdem wert :-)
Für die Anwendungen, an denen wir interessiert sind, gibt es zwei Arten von unendlich-dimensionalen Vektorräumen, die interessant sind:
Wir können uns Vektoren vorstellen, die unendlich (potentiell) lang sind, also Folgen von Zahlen
\[(a_i)_{i \in \mathbb{N}} = (a_1, a_2, ...)\]
Die Addition und Multiplikation mit Zahlen würden wir genauso definieren, wie für endlich-lange Vektoren. Die Skalarmultiplikation können wir auch analog definieren
\[\big\langle (a_i)_{i \in \mathbb{N}}, (b_i)_{i \in \mathbb{N}} \big \rangle := \sum_{i=1}^\infty a_i \cdot b_i,\]
wobei man natürlich aufpassen muss, ob das auch wirklich konvergiert. In den Fällen, die uns interessieren (z.B. Fourierreihen von sinnvollen Funktionen) ist das in der Regel der Fall (und wenn nicht ignorieren wir technische Probleme und Einschränkungen einfach).
Wozu ist’s gut?
Ein Beispiel für solche Folgenräume sind Polynome (von potentiell unbeschränktem Grad). Die Objekte, die uns interessieren, sind Funktionen der Form \[ x \mapsto a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots \] Addiert man mehrere davon, so kann man die \(x\)-e ausklammern und man sieht, dass man eigentlich nur die Koeffizientenfolge addieren muss. Gleiches gilt für die Multiplikation mit Zahlen. Wenn man den Grade nicht a priori beschränkt, so erhält man einen unendlich-dimensionalen Vektorraum.
Später werden für uns auch noch Fourier-Reihen interessant sein, die man ganz ähnlich als \[ x \mapsto z_0 + z_1 e^{-i x} + z_2 e^{-2ix} + z_3 e^{-3ix} + \cdots \] schreiben kann.
Allgemein sind Kombinationen von Funktionen in der Form \[ f(x) = \lambda_1 b_1(x) + \lambda_1 b_1(x) + \lambda_3 b_3(x) + \cdots \] für feste Funktionen \(b_1,b_2,b_3...\) interessant. Die Koeffizientenfolge \((\lambda_i)_{i \in \mathbb{N}}\) ist dann ebenfalls ein unendlich langer Vektor. Addition und Multiplikation der Funktionen vom Typ wie \(f\) führt zu der Addition und Multiplikation der Koeffizienten (wie bei profanen Vektoren), da man auch hier einfach die \(b\)-s ausklammern kann.
Wozu sowas gut ist, verschieben wir in den nächsten Abschnitt.
Disclaimer: Zunächst eine Bemerkung zum Aufbau der ganzen Vorlesung. In der Mathematik gibt es oft die schlimmsten Probleme, wenn man mit unendlichen Objekten hantieren muss. Wenn wir mit Funktionenräume arbeiten, stellen sich oft Fragen nach der Existenz von Grenzwerten, die leider nicht einfach zu beantworten sind. Alleine die Definition eines Skalarproduktes erfordert eine Menge fortgeschrittener mathematischer Konzepte (z.B. Lebesgue-Integration, Equivalenzklassen modulo Nullmengen, usw.). Wir ignorieren hier alles “technischen” Schwierigkeiten und schauen uns nur das Grundprinzip an. Wenn Sie das richtig lernen möchten (mit sauberen Definitionen und Beweisen, dass das auch alles stimmt), müssen Sie eine Mathematikveranstaltung besuchen.
Nach dieser Vorrede: Was für Konzepte gibt es für Vektorräume von Funktionen (statt geometrischen Pfeilen)?
Eine kontinuierliche Funktion (also mit reellen Zahlen als Definitionsgebiet) kann auch als Vektor in einem Vektorraum aufgefasst werden. Schauen wir uns allgemein das folgende an:
Sei \(\Omega \subset \mathbb{R}^d\) eine beliebige Teilmenge des \(d\)-dimensionalen Raumes (\(\mathbb{R}^d\) ist auch ein Vektorraum, aber nicht der, um den es hier geht). Wir betrachten nun die Menge \(V\) aller Funktionen \[ V = \{ f | f: \Omega \rightarrow \mathbb{R} \} \] Die Menge aller solcher Funktionen ist ein Vektorraum, wenn wir die naheliegende Defintion\((f+g)(x) = f(x)+g(x)\) und \((\lambda \cdot f)(x) = \lambda \cdot f(x)\) benutzen (auch “punktweise Addition/Multiplikation genannt). Die Axiome nachzurechnen ist hinreichend langweilig da offensichtlich (und abgeschlossen ist es auch). Interessanter ist vielleicht die Intuition, dass eine kontinuierliche Funktion eine Verallgemeinerung einer diskreten Funktion sind (mit Definitionsgebiet als Teilmenge von \(\mathbb{Z}^d\), also z.B. \(\{1,2,3,...,n\}\) für ein Intervall und \(d=1\)):
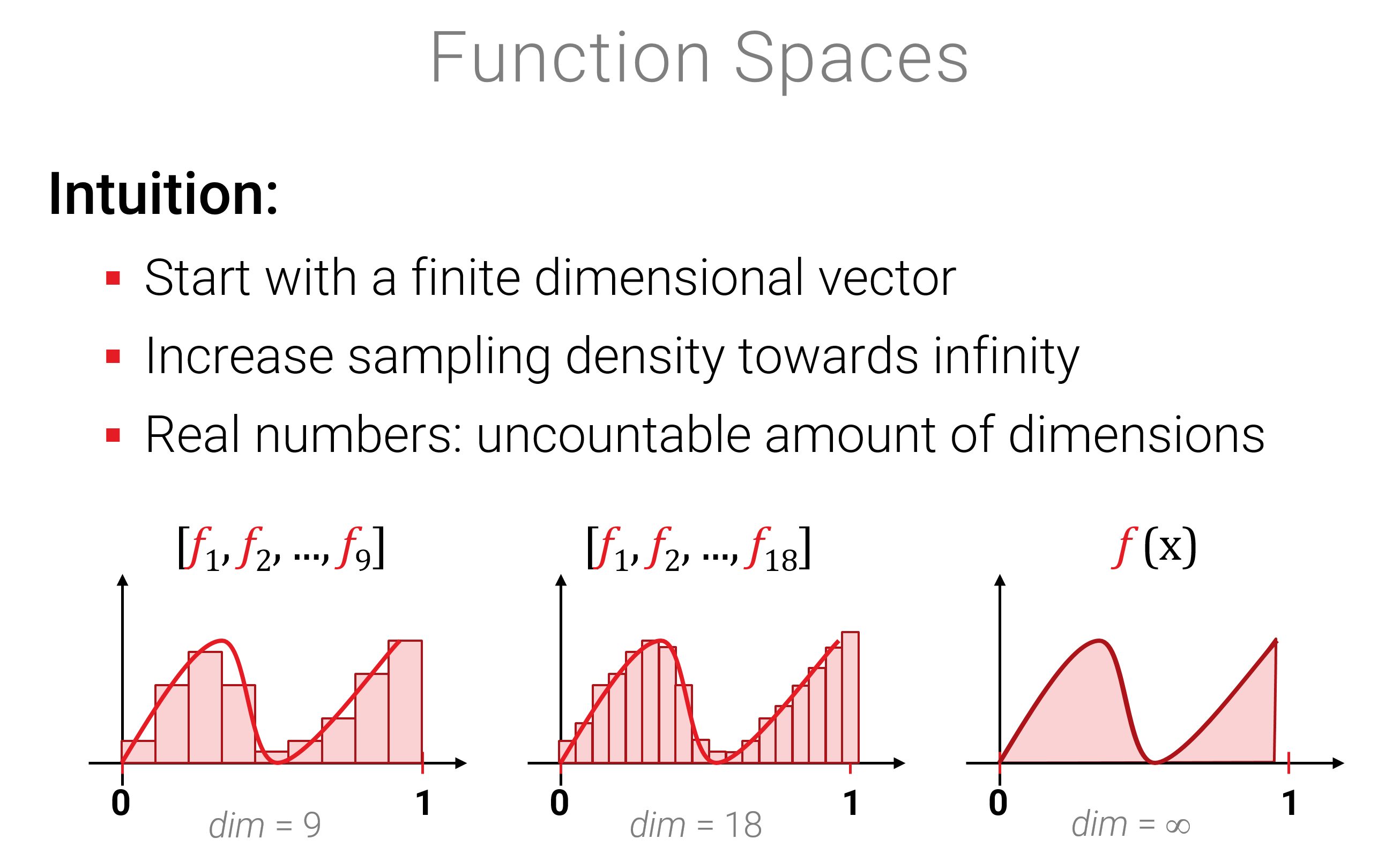
In vielen Anwendungen möchten wir nun Funktionen modellieren, z.B. die Bahnen von 8 Planeten um die Sonne über die Zeit als Funktion \(\mathbb{R} \rightarrow \mathbb{R}^{24}\) (\(24=3 \times 8\); die Planeten fliegen in 3D. Und ja - es wahren früher mal 9, das wahren noch Zeiten!). Wir können nun solche Funktionen als Vektoren in einem unendlich-dimensionalen Vektorraum auffassen. Das erlaubt uns, Funktionen zu addieren und zu skalieren (klingt nicht so spektakulär – aber wait for it…).
Was uns noch fehlt, ist eine sinnvolle Definition des Skalarproduktes. Aus der Anschauung, dass es eigentlich “normale” Vektoren sind, die nur sehr hoch aufgelöst sind, können wir einen Skalarprodukt via Grenzwertübergang konstruieren. Die diskrete Summe wird dabei einfach durch ein Integral ersetzt.
Das Standardskalarprodukt auf einem Funktionenraum mit Funktionen \(\mathbb{R}^d \supseteq \Omega \rightarrow \mathbb{R}\) ist definiert als:
\[ \langle f, g \rangle := \int_\Omega f(\mathbf{x}) \cdot g(\mathbf{x}) d\mathbf{x} \]
Das es alle Axiome erfüllt, ist leicht nachgerechnet. (Die Konvergenz ist ein anderes Problem, dazu muss man die zulässige Menge von Funktionen einschränken; wir ignorieren das Problem hier einfach; für “physikalisch realistische” Funktionen ist das kein Problem.)
Mit dem Skalarprodukt kann man die Norm \[||f|| = \sqrt{\langle f, f \rangle}\] (das Äquivalent zur “Länge”) einer Funktion messen und auch den “Winkel” zwischen zwei Funktionen \[\cos \angle f,g = \frac{\langle f , g \rangle}{||f||,||g||}\] messen. Die quantiativen Werten, insbesondere für “Winkel” sind allerdings für viele Modelle schwer zu interpretieren (wie sehen Funktionen aus, die einen Winkel von \(42^\circ\) zueinander haben?). Ein Spezialfall, der häufig benötigt wird, ist der Fall von \(90^\circ\): Wenn Funktionen orthogonal aufeinander stehen, dann bedeutet dies, dass die Projektion des einen Vektors (Funktion) auf den anderen Vektor (die andere Funktion) null ist - wenn man sich also in die eine Richtung im (Funktionen-)Raum bewegt, dann ändert das nichts in Bezug auf die andere Richtung. Hier ein Bild, wie man orthogonale Funktionen konkret aussehen können:
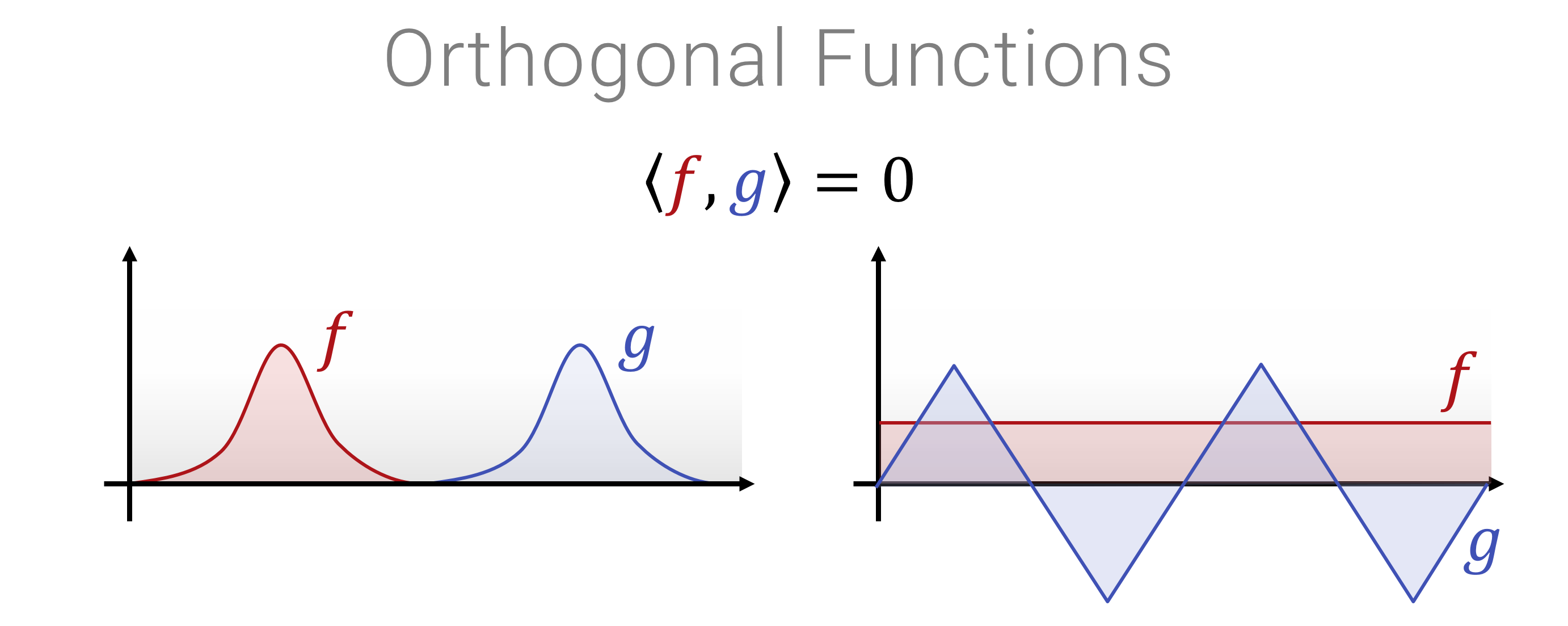
Im Computer können wir offensichtlich nicht mit echten Funktionen als Vektoren rechnen, da man, um eine beliebige Funktion zu repräsentieren, unendlich viele Zahlen speichern müsste. Was man daher macht, ist eine Approximation zu verwenden. Im wesentlichen gibt es \(2\frac{1}{2}\) Möglichkeiten:
Möglichkeit 1: FD - Alles ist ein Array. Wir repräsentieren die Funktion einfach, wie oben in der Abbildung angedeutet, als Array von \(d\) Zahlen und rechnen mit Vektoren aus \(\mathbb{R}^d\). Mit Werten zwischen diesen diskreten Werten rechnen wir einfach nie (die Frage ist nicht erlaubt). In der Anwendung auf die Diskretisierung von (partiellen) Differentialgleichungen nennt man das ganze auch “finite-Differenzen (FD)” Verfahren
Möglichkeit 1.5: Prozedurale Kodierung. Die diskrete Struktur ist manchmal ungewünscht - man kann nicht immer vermeiden, mit Zwischenwerten zu rechnen. Was kann man tun, um kontinuierliche Funktionen zu erhalten? Hier ist ein sehr algemeiner (der allgemeinste!) Ansatz: Wir schreiben einen Algorithmus, der einen Zahl \(x\) als Eingabe bekommt, und \(f(x)\) berechnet. Damit kann man sehr viele Funktionen sehr genau repräsentieren, aber man kann mit der Repräsentation nicht wirklich algebraisch rechnen, da man für algebraische Umformungen den Programmcode verstehen müßte. Viel Glück.
Diese Möglichkeit ist also nur “eine halbe” Lösung; sie ist zu mächtig, um mit Funktionen als Variablen rechnen zu können. Es spricht aber nichts dagegen, fixe Funktionen so zu definieren, und dies auch zu benutzen. Damit bildet dies das Fundament für die zweite “richtige” Lösung:
Möglichkeit 2: FEM - Linearer Ansatz / Basisfunktionen. Die Eleganteste Variante ist es, die gewünschte Funktion als Linearkombination von Basisfunktionen darzustellen:
\[ f(x) \approx \sum_{i=1}^d \lambda_i b_i(x) \]
Wobei \(b_1,..,b_d\) eine zuvor ausgewählte Liste von Basisfunktionen ist. Jede Funktion hat nun einen endlich-dimensionalen Koordinatenvektor \(\boldsymbol{\lambda} \in \mathbb{R}^d\). Trotzdem ist die Funktion kontinuierlich (und kann auch glatt sein), indem man geeignete kontinuierliche (glatte) Basisfunktionen wählt. Deren Wert berechnet man dann prozedural (also mit einem Algorithmus, der für die spezielle(n) Basisfunktion(en) designt wurde). Der lineare Ansatz ist auch die Basis (no pun intended) für finite-Elemente Methoden (FEM) (z.B. ebenfalls für die Lösung von partiellen Differentialgleichungen).
Beliebte Basisfunktionen für theoretische Anwendungen sind z.B. Monome \[ 1,x,x^2,x^3,... \] oder die reelle Fourier-Basis \[ 1, \sin(x), \cos(x), \sin(2x), \cos(2x), ... \] oder noch (vielleicht noch öfter) die komplexe Fourier-Basis \[ 1, \exp(-ix), \exp(-2ix), \exp(-3ix), ... \]
Für praktische Anwendungen sind Basisfunktionen aus Tiefpassfiltern sehr beliebt (warum die so heißen, sehen wir erst gegen Ende, in Kapitel 6), z.B. B-Spline Funktionen, die Gaußsche Glockenkurven mit stückweise-polynomiellen Funktionen von unterschiedlichem Grad annähern:
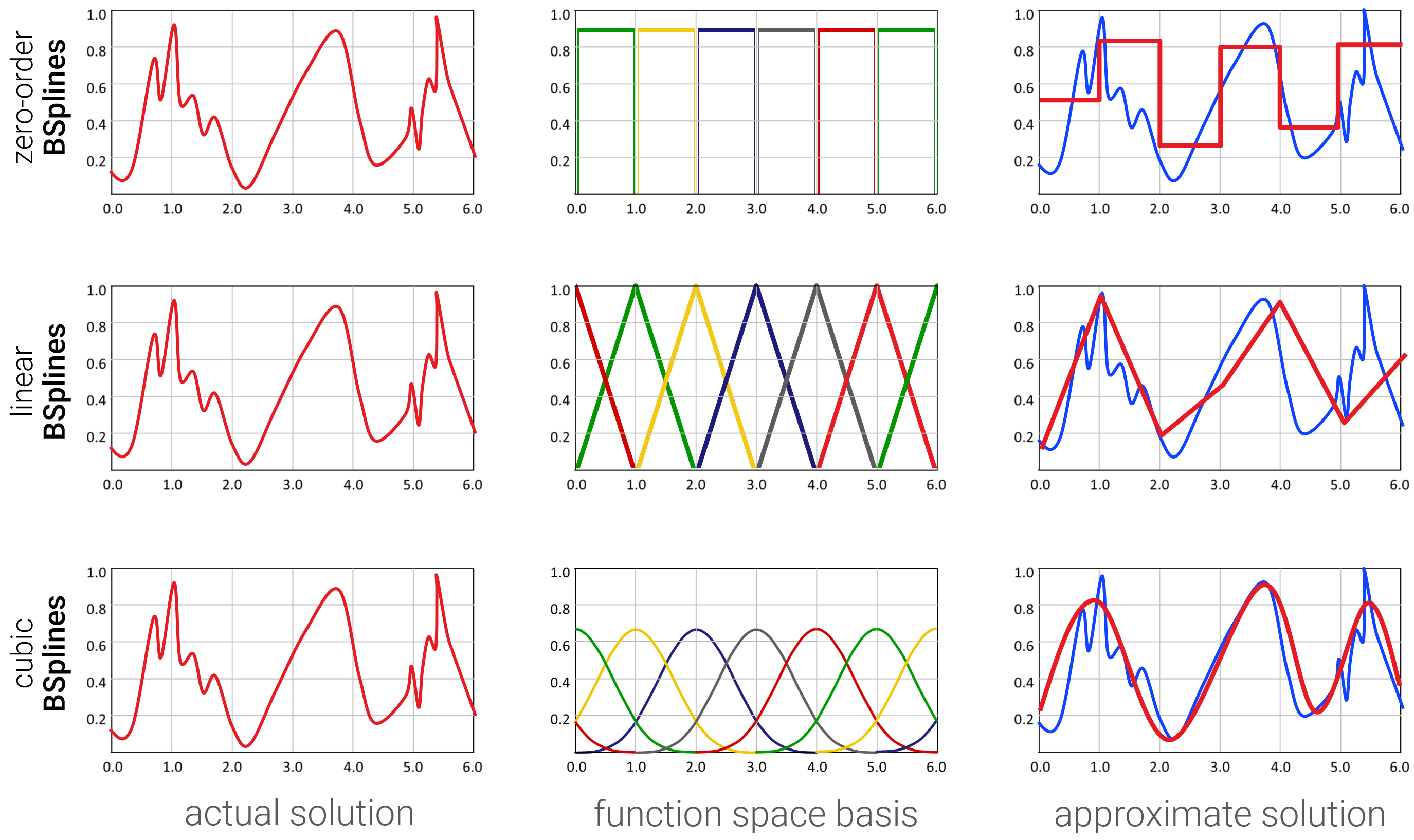
Aus theoretischer Perspektive definiert man in der Regel zunächst einen “echten”, überabzählbar-unendlichen Funktionenraum, wie z.B. die Funktionen, die vom Intervall \([0,1]\) in die reellen Zahlen abbilden. Danach muss man einiges an theoretischem Aufwand betreiben, um darauf sinnvoll Skalarprodukte zu definieren. Eine typische Lösung ist der “Hilbert-Raum” \(L_2\), in dem das Standard-Skalarprodukt immer konvergiert.
Danach wählt man eine geeignete Basis. Die Standardbasis, wie wir sie oben definiert haben, ist dabei weniger geeignet, da es schwer fallen kann, diese (obschon wir die Existenz bewiesen haben) explizit zu konstruieren. Einfacher geht es mit einer Schauder-Basis, die versucht, die Funktionen mit einer Reihenentwicklung anzunähern:
\[ f(x) = \lim_{n \rightarrow \infty } \sum_{i=1}^n \lambda_i b_i(x) \]
Dabei sind die \(b_i\) geeignete Basisfunktionen. Für den Hilbertraum \(L_2\) für die o.g. reellen Funktionen auf dem Intervall \([0,1]\) sind z.B. die Fourierbasisfunktionen \(\{1, \sin (2\pi k x), \cos (2 \pi k x) | k=1,2,3,...\}\) eine sinnvolle Wahl. Mit diesen kann man alle Funktionen in \(L_2\) konstruieren (wobei das Ähnlichkeitsmaß so definiert ist, dass theoretische Approximationsfehler nicht ins Gewicht fallen).
Damit hätten wir den (überabzählbar-unendlich-dimensionalen) kontinuierlichen Funktionenraum \(L_2\) auf einen abzählbar-unendlich-dimensionalen Folgenraum (mit dem sinnigen Namen \(\ell_2\)) heruntergehandelt.
Da man zuvor sichergestellt hat, dass die Folgen auch tatsächlich konvergieren, wissen wir auch, dass wir sie irgendwann abschneiden können, und der Fehler nicht beliebig groß wird. Damit wären wir zurück am endlich-dimensionalen Raum \(\mathbb{R}^d\), den wir halbwegs verstehen können, und auch am Rechner sinnvoll nutzen können.
Übrigens: Wo man die Reihenentwicklungen abschneiden kann, hängt natürlich von der Funktion ab, die wir repräsentieren wollen (und der Basis, die wir benutzen). Die Frage, wo wir die Fourierbasis abschneiden können und wollen, ist dabei wesentlich interessanter, als man an dieser Stelle vielleicht denkt. Mehr dazu in Kapitel 6.
Aufgabe 1.1: Ich möchte eine Ebenengleichung (in 3D) durch drei Punkte legen. Wie mache ich das?
Aufgabe 1.2: Bestimmen sie eine implizite Funktion, die die folgenden geometrischen Primitive beschreibt:
Aufgabe 1.3: Nehmen Sie an, dass wir einen abstrakten Vektorraum \(V\) mit Körper \(F\) mit einer endlichen Basis \(B=\{\mathbf{b}_1, ...,\mathbf{b}_d\}\) haben. Man kann nun jeden Vektor \(v\in V\) als eine Linearkombination \[v = \sum_{i=1}^d \lambda_i \cdot b_i\] darstellen. Zeigen Sie, dass die Zuordnung \[v \mapsto \left(\begin{array}{c}\lambda_1\\ \vdots \\ \lambda_d \end{array}\right)\] ein Isomorphismus zwischen \(V\) und \(F^d\) ist. Benutzen Sie dazu die im Text beschriebenen Eigenschaften von Basen und Vektorräumen.
Aufgabe 1.4: Zeigen Sie, das die komplexe Fourierbasis orthogonal ist. Das heißt, für die Funktionen \[b_k: [0,2\pi] \rightarrow \mathbb{C},\ \ \ \ b_k(x)= e^{-i k x}\] gilt: \[\langle b_m, b_n \rangle = \delta_{m,n}\] wobei die diskrete Deltafunktion wie üblich als \(\delta_{m,n} = 1\) für \(m=n\) und \(\delta_{m,n} = 0\) für \(m \neq n\) definiert ist.
tl;dr – Wir wechseln das Koordinatensystem
In diesem Kapitel schauen wir uns Funktionen an, die Vektoren auf Vektoren abbilden:
\[ f: V_1 \rightarrow V_2\]
Einfache Zahlen zählen dabei als 1D Spezialfall von Vektoren; formal ist \(F^1\) (also in der Regel \(\mathbb{R}^1\)) auch ein Vektorraum.
Man kann sich hier natürlich sehr komplizierte Funktionen vorstellen (wir wissen ja sogar, dass es jede Menge unberechenbare Funktionen gibt). Diejenigen Funktionen, die man gut verstehen kann, ist allerdings leider relativ beschränkt.
Die wichtigste Klasse von Funktionen, die man mehr oder weniger komplett durchschaut hat, und für die man effiziente Algorithmen hat, um so ziemlich jede Fragen über die Funktion berechnen zu können, sind die linearen Funktionen. Und dies wollen wir uns nun genauer anschauen. Zum Schluss schauen wir uns auch kurz quadratische Funktionen an; da deren Gradientenfeld (also die erste Ableitung) linear ist, tauchen diese auch häufig auf, insbesondere im Kontext von Optimierungsproblemen (an Extremstellen verschwindet die Ableitung).
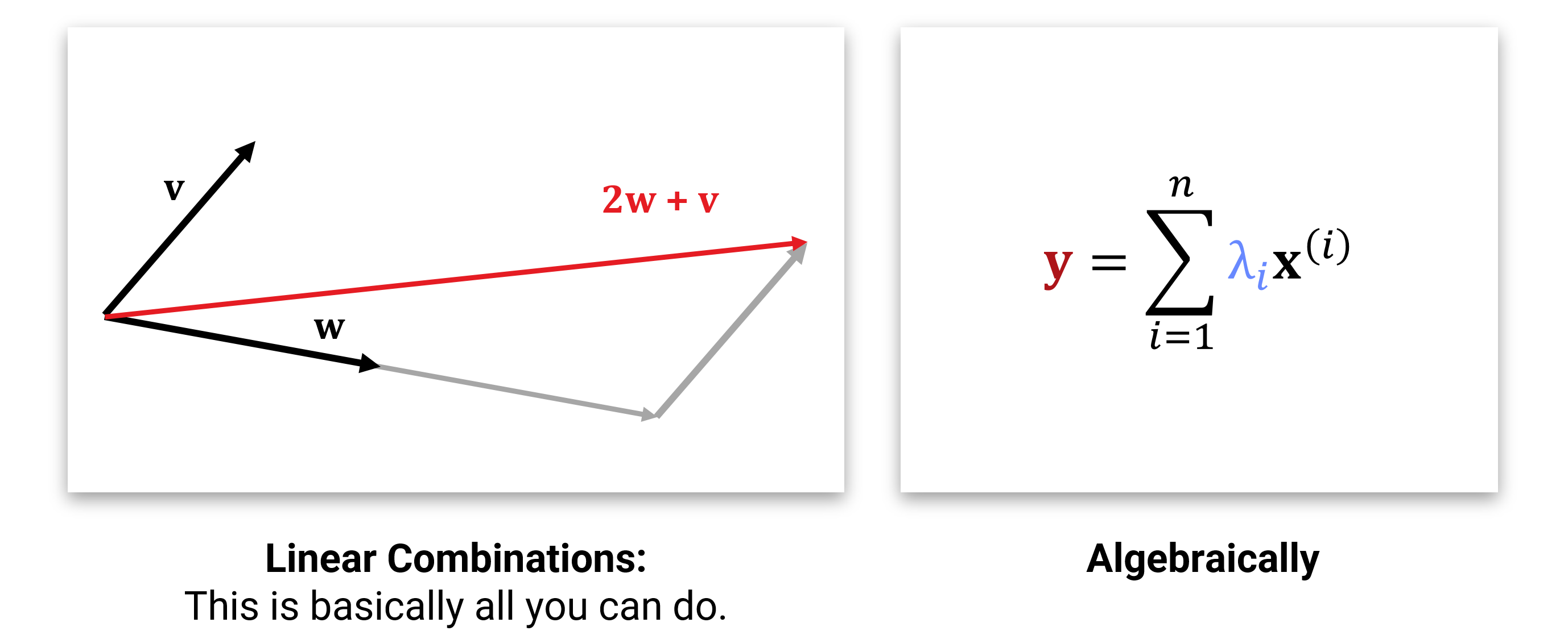
Wir haben ja bereits gesehen, dass man in einem Vektorraum nicht viel anderes machen kann, als Vektoren linear zu kombinieren:

Für eine fixe, gegebene Menge von Vektoren \(\mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d\) bezeichnet man die Abbildung
\[ \left(\begin{array}{c}\lambda_1\\ \vdots \\ \lambda_d \end{array}\right) \mapsto \sum_{i=1}^n \lambda_i \cdot \mathbf{x}_i \]
als lineare Abbildung. Anders gesagt, geht es um Abbildungen, bei denen jede Ausgabe ein rein lineares Polynom in den \(\lambda_i\) ist (also nur Terme erster Ordnung enthält; Addieren von Konstanten oder Multiplikation von mehreren Lambdas miteinander ist verboten).
Wir schreiben dies in der Regel als Matrix-Vektor-Multiplikation: Die neuen Vektoren \(\mathbf{x}_i\) werden in die Spalten einer Matrix (=2D Array) geschrieben:
\[ \mathbf{X} = \left( \begin{array}{ccc} | & & | \\ \mathbf{x}_1 & \cdots & \mathbf{x}_d \\ | & & | \end{array} \right) = \left( \begin{array}{ccc} x_{1,1} & \cdots & x_{d,1} \\ \vdots & \ddots & \vdots \\ x_{1,n} & \cdots & x_{d,n} \end{array} \right) \]
und die lineare Abbildung schreibt man als Matrix-Vektor-Multiplikation
\[ \mathbf{X} \cdot \boldsymbol{\lambda} = \sum_{i=1}^n \lambda_i \cdot \mathbf{x}_i \]
with \[ \mathbf{y} = \mathbf{X} \cdot \boldsymbol{\lambda} \]
Wir können dies auch in Skalarer Notation (“Tensor”-Notation, wenn man möchte) schreiben, als:
\[ y_{j} = \sum_{i=1}^n \sum_{j=1}^d x_{i,j} \cdot \lambda_{i}. \]
Vorstellen kann man sich das so, dass die \(\lambda_1,...,\lambda_d\) Koordinaten für neue Richtungen \(\mathbf{x}_1,...,\mathbf{x}_d\) sind:

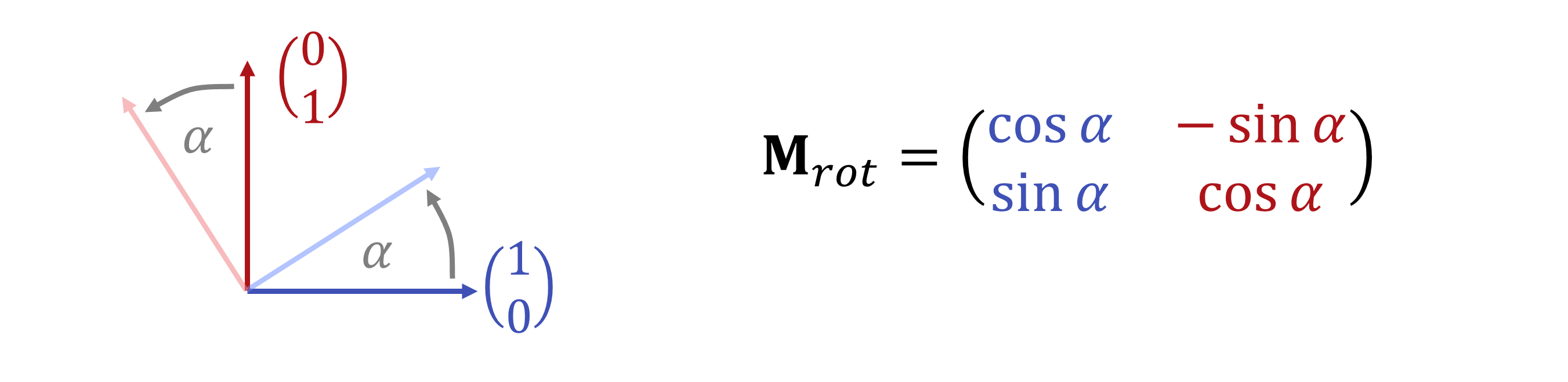
Abbildungen, die multi-variate Polynome mit maximalem Grad \(1\) sind (also konstante und lineare Terme enthalten), nennt man affine Abbildungen. Sie hätten (im endlich-dimensionalen) die Form:
\[\mathbf{y}(\boldsymbol{\lambda}) = \mathbf{X} \cdot \boldsymbol{\lambda} + \mathbf{t}\]
mit einem festen Verschiebungsvektor \(\mathbf{t}\in \mathbb{R}^n\) (Rest wie zuvor).
Mit Vektoren (und später auch Matrizen) kann man algebraisch rechnen, wie man es aus der Schule von Termumformung mit “normalen” Zahlen kennt. Für das Lösen von Gleichungen und Problemen ist es natürlich sehr wichtig, dies gut zu beherrschen. Dazu muss man die verschiedenen Regeln (auswendig) lernen und üben, dies für Termumformungen anzuwenden.
Es gibt verschiedene “Rezepte”, wie man das ganze strukturiert und angeht. In der Vorlesung wurden zwei übliche Ansätze vorgestellt: Matrix Algebra (siehe Vorlesungsfolien 03 - Lineare Abbildungen ab Seite 17) und die Tensor-Notation (Vorlesungs Folien Addendum Co- und Kontravarianz auf Seite 18/19).
Die Abstrakte Definition haben wir bereits in Abschnitt 1 gesehen: Abstrakt sind lineare Abbildungen Homomorphismen zwischen Vektorräumen. Das heißt für eine Funktion:
\[ f: V_1 \rightarrow V_2\]
zwischen zwei Vektorräumen \(V_1\) und \(V_2\) mit Körper \(F\) muss für alle \(\mathbf{x},\mathbf{y} \in V_1, \lambda \in F\) gelten, dass
\[f(\mathbf{x}+\mathbf{y})=f(\mathbf{x})+f(\mathbf{y}), \text{ und}\\ f(\lambda \cdot \mathbf{x})=\lambda \cdot f(\mathbf{x}).\]
Man kann (relativ einfach) zeigen, dass sich alle diese Abbildungen als Matrix darstellen lassen, wenn man es mit endlich-dimensionalen Räumen \(V_1,V_2\) zu tun hat (siehe Übungsaufgaben). Hauptvorteil der abstrakten Definition aus Anwendungsperspektive ist sicher, dass unendlich-dimensionale Vektorräume, insbesondere Funktionenräume, mit abgedeckt sind.
Affine Abbildungen: Eine Abbildung heißt affin (statt linear)…erfüllen die gleichen Definition, wenn e
In der Praxis stellt sich natürlich die Frage, was das Analogon zu Matrix bei Funktionenräumen ist. Wir arbeiten in dieser Vorlesung (wie die meisten Ingenier*innen und Naturwissenschaftler*innen) nur mit Räumen, für die es eine Schauerbasis gibt, die man also über Folgen beschreiben kann. In dem Fall besteht die “Matrix” aus einer Folge von Funktionen, und ein Vektor kann man als Folge von Koeffizienten darstellen.
Nehmen wir nun also an, dass die Menge \(\{b_1,b_2,...\}\) von Funktionen \(b_i:\mathbb{R}^d \supseteq \Omega \rightarrow \mathbb{R}\) eine orthogonale Schauderbasis für einen (geeigneten) Funktionenraum (von Funktionen, die von \(\Omega\) nach \(\mathbb{R}\) abbilden) ist. Dann können wir die Koordinatenfolge \(\lambda_1,\lambda_2...\) einer Funktion \(f\) einfach über das Skalarprodukt
\[ \lambda_i = \langle f, b_i \rangle \]
bestimmen. Die neue Funktion erhält man nun, indem man eine allgemeine lineare Abbildung auf diese Koordinaten anwendet, also:
\[ \lambda_j' = \sum_{i=1}^\infty m_{i,j} \lambda_i \]
Die finale Funktion bekommen wir dann, indem wir wieder die Linearkombinationen der Basisfunktionen bilden:
\[ Mf = \sum_{i=1}^\infty \lambda_i'\cdot b_i = \sum_{i=1}^\infty \left( \sum_{i=1}^\infty m_{i,j} \langle f, b_i \rangle \right) \cdot b_i \]
Kurz gefasst, kann man hier die Abbildung als eine Matrix mit (abzählbar) unendlich vielen Einträgen darstellen (man kann sich vorstellen, dass die Matrix nach rechts-unten offen ist).
\[ M \text{ "=" } \left( \begin{array}{rrr} m_{1,1} & m_{2,1} & \cdots \\ m_{1,2} & m_{2,2} & \\ \vdots & & \ddots \end{array} \right) \]
Die Einträge werden dabei immer weniger wichtig für das Endergebnis. Es gibt hier natürlich ein paar konzeptionelle Probleme (z.B., in welcher Reihenfolge man die Doppelsumme oben berechnen kann/muss, damit sie konvergiert) - wir gehen hier nicht tiefer darauf ein.
In der Praxis schneiden wir die Basis und die Koeffizientenfolge immer irgendwo ab - unser Rechner hat leider nicht unendlich viel Speicher.
Wenn wir mit linearen Funktionen rechnen, stellt sich auch die Frage, wie man diese Umkehren kann. Stellen wir uns also eine Abbildung
\[\begin{eqnarray} \mathbf{y} = f(\mathbf{x}) &=& \sum_{i} x_i \mathbf{m}_i \\ &=& \sum_{i} \sum_{j} x_i m_{i,j} \end{eqnarray}\]
vor. Nun ist es hier aber so, dass wir das Ergebnis \(\mathbf{y}\) kennen, sowie die Matrix \(x_{i,j}\), die die lineare Abbildung definiert; die Frage ist nun, welche “Koordinaten” \(\lambda_1,\lambda_2,...\) wir benutzen müssen, um das richtige Ergebnis \(\mathbf{y}\) zu erhalten. Wir wollen also die Gleichung \[ \mathbf{y} = \mathbf{M} \mathbf{x} \] nach \(\mathbf{x}\) auflösen.
Da stellen sich zwei bis drei Fragen (je nach Praxisaffinität): - Geht das überhaupt? - Wenn ja, wie macht man es? - Geht es in der Praxis wirklich, oder kann noch was schief gehen.
Die Antworten sind offensichtlich: 1. kommt drauf an, 2. es gibt Verfahren wie Sand am Meer, 3. kommt drauf an.
Wie wir in Kapitel 1 schon gesehen haben, ist die Menge \(\{\mathbf{Mx}| x_1,x_2,... \in \mathbb{R}\} = \operatorname{span}\{\mathbf{m}_1,\mathbf{m}_2,...\}\) ein Unterraum des Vektorraums aller möglichen Ergebnisse. Dieser hat eine feste Dimension (den Rang von \(\{\mathbf{m}_1,\mathbf{m}_2,...\}\)). Das LGS ist offensichtlich dann und nur dann lösbar, falls \(\mathbf{y} \in \operatorname{span}\{\mathbf{m}_1,\mathbf{m}_2,...\}\).
Beweisskizze: Nehmen wir an, dass \(\mathbf{y} \not \in \operatorname{span}\{\mathbf{m}_1,\mathbf{m}_2,...\}\). Dann gibt es kein Gewichtsvektor \(\mathbf{x}\), mit dem man die \(\mathbf{m}_i\) zu \(\mathbf{y}\) kombinieren könnte. Tough luck. Andersherum: Wenn \(\mathbf{y}\) in der linearen Hülle ist, dann kann man per Definition \(\mathbf{y}\) aus \(\mathbf{m}_1,\mathbf{m}_2,...\) linear kombinieren. Also alles offensichtlich.
Struktur des Lösungsraumes
Wenn eine solche Lösung existiert, muss die nicht unbedingt eindeutig sein. Wieviele Lösungen es gibt, zeigt die folgende Analyse:
Lösen wir zuerst das Problem \(\mathbf{M} \mathbf{x} = \mathbf{0}\). Die Menge dieser Lösungen nennt man auch den Kern von \(\mathbf{M}\) (geschrieben \(\operatorname{ker}(\mathbf{M})\)). Diese Lösungen bilden einen Vektorraum, weil - Sie aus Vektoren besteht (also gelten alle Axiome). - Weil Summen und Vielfache von Lösungen \(\mathbf{x}_1,\mathbf{x}_2\) auch Lösungen sind, weil \(\mathbf{M}\) linear ist: \[ \mathbf{M}(\mathbf{x}_1 + \lambda \mathbf{x}_2) = \mathbf{M}\mathbf{x}_1 + \lambda\mathbf{M}( \mathbf{x}_2) = \mathbf{0} + \lambda \mathbf{0} = \mathbf{0} \]
Wenn es nun eine Lösung \(\mathbf{x}'\) für das vollständige Problem \(\mathbf{M} \mathbf{x} = \mathbf{y}\) gibt, dann kann kann man jedes Element von \(\operatorname{ker}(\mathbf{M})\) zu dieser Lösung addieren, und erhält weiterhin eine gültige Lösung (nachdem man \(\mathbf{M}\) ausklammert, hat man nur einen Nullvektor draufaddiert; das ändert natürlich nix).
Zusammengefaßt: Lösungen von LGS sind affine Unterräume des Vektorraumes \(V_1\) (der Eingabe von \(\mathbf{M}\)).
Kann man sich vorstellen als: Punkte, Geraden, Ebenen oder Hyperebenen mit verschieden hoher Dimension (bis hin zu \(\operatorname{dim}(V_1)\), auch bekannt als “alles”).
Wenn man eine \(d \times d\) Matrix hat, die von einem Vektorraum \(V\) wieder in \(V\) abbildet, mit \(\operatorname{dim}(V) = d\) (man nennt das auch einen Endomorphismus), dann kann man sich fragen, ob es hier eine umkehrabbildung \(\mathbf{M}^{-1}\) gibt, die \(\mathbf{M}\) rückgängig macht, also \(\mathbf{M} \mathbf{M}^{-1} = \mathbf{I}\) (wobei \(\mathbf{I}\) die Einheitsmatrix ist, die die Eingabe unverändert durchreicht).
Man kann sich leicht überlegen, dass dies der Fall sein muss genau dann, wenn \(\operatorname{span}(\mathbf{m}_1,...,\mathbf{m}_d) = V\) (oder anders gesagt: genau dann, wenn \(\operatorname{rank}(M)=d\)).
In allen anderen Fällen, \(0\leq \operatorname{rank}(M) < d\), ist die Matrix nicht invertierbar. Wir werden im nächsten Unterabschnitt sehen, dass das in der Praxis eine eher idalisierte Vorstellung ist. Zuvor wollen wir nochmal kurz darauf schauen, was im nicht-invertierbaren Fall passiert.
50 Shades of Non-Invertible
Das eine Matrix nicht invertierbar ist, heißt noch nicht unbedingt, dass man keine Informationen über die Eingabe aus der Ausgabe rückschließen kann; es heißt nur, dass die Abbildung nicht eindeutig (injektiv) ist, also Information verloren geht.
Es ist sehr nützlich, genauer zu verstehen, wie bei linearen Abbildungen überhaupt Informationen verloren gehen. The upshot is: Man verliert immer ganze Dimensionen (alles was entlang eines Basisvektors liegt) auf einmal. Der Informationsverlust kann auf eine Reduktion der Dimension heruntergebrochen werden, so dass nur ein Unterraum erhalten bleibt.
Genauer sieht es so aus: Alles in \(\ker(\mathbf{M})\) wird auf \(\mathbf{0}\) abgebildet, und ist damit unwiederbringlich verloren. Alle Vektoren, die orthogonal zum Kern stehen, bleiben erhalten (wenn man davon die lineare Hülle bildet, um einen orthogonalen Unterraum zu erhalten, bezeichnet man dies auch als das orthogonale Komplement vom Kern, \(\ker(\mathbf{M})^\perp\)). Es gilt also für jede lineare Abbildung zwischen endlich-dimensionalen Vektorräumen:
\[\mathbf{M}:V_1 \rightarrow V_2,\] dass \[\dim(V_1) = \dim(\ker(\mathbf{M})) + \dim(\ker(\mathbf{M})^\perp).\] Eingeschränkt auf den Raum \(\dim(\ker(\mathbf{M})^\perp)\) als Eingabe ist \(\mathbf{M}\) injektiv (also invertierbar).
Um dies zu beweisen, muss man sich noch überlegen, dass Vektoren, die orthogonal zu Kern stehen, nicht mehrdeutig abgebildet werden können. Das ist nicht besonders schwer (es ist wieder das Argument mit dem Ausklammern), aber wir sparen uns das hier.
Man kann das ganze auch in \(V_2\) betrachten. Hier ist \(\operatorname{im}(\mathbf{M}) := \{\mathbf{y} \in V_2| \exists \mathbf{x} \in V_1: \mathbf{M}\mathbf{x} = \mathbf{y}\}\) das sogennante “Bild” von \(\mathbf{M}\), also die Menge aller Vektoren, die man aus Eingaben aus \(V_1\) mit Hilfe von \(\mathbf{M}\) bauen kann. Nun gilt das folgende:
\[ \dim(\ker(\mathbf{M})^\perp) = \dim(\operatorname{im}(\mathbf{M}))(M),\]
weil \(\mathbf{M}\) sonst nicht in dem komplementraum invertierbar sein könnte (Beweis lassen wir aus), und damit die bekannte “Dimensionsformel”
\[\dim(V_1) = \dim(\ker(\mathbf{M})) + \dim(\operatorname{im}(\mathbf{M})).\]
Nochmal anders kann man es auch über den Rang formulieren:
\[\operatorname{rank}(\mathbf{M}) = \dim(\operatorname{im}\mathbf{M})\] und \[\dim(\operatorname{ker}\mathbf{M}) = \dim(V_1) - \operatorname{rank}(\mathbf{M}).\]
Noch eine Bemerkung zur Notation: Wenn der Kern nicht-trivial ist (also nicht Dimension \(0\) hat), bzw. äquivalent dazu, \(\operatorname{rank}(\mathbf{M})<\dim V_1\), dann nennt man \(\mathbf{M}\) auch singulär (im Englischen “singular” oder “rank-deficient”).
Was sollte man sich merken? - Lineare Abbildungen bilden immer Unterräume invertierbar auf Unterräume ab; diese müssen die gleiche Dimension haben. - Alles andere geht verloren (\(V_1\)) bzw. wird nie erreicht (\(V_2\)). - Jedesmal wenn man die die Dimension \(\dim(\operatorname{im}(\mathbf{M})) = \operatorname{rank}(\mathbf{M})\) um eins reduziert wird, verliert man eine ganze “Richtung” aus der Eingabe.
Anders gesagt: Wenn man sich fragt, wieviel Informationen man nach einer linearen Abbildung noch rekonstruieren kann, dann fragt man danach, wieviele linear unabhängige Richtungen (diese kann man, wie wir gleich sehen obdA. orthogonal wählen), man noch rekonstruieren kann.
Das ist tatsächlich nützlich zu wissen (nicht nur Algebra-Gymnastik), da man viele Beobachtungen oder Messvorgänge als lineare Operationen (zumindest näherungsweise) Modellieren kann. Wenn man also wissen will, was man nicht weiss, dann ist das oben gesagte die theoretische Antwort.
Die theoretische. In der Praxis ist es natürlich immer nochmal ein bischen schwieriger. Und das schauen wir uns als nächstes an.
Wie können wir in der Praxis lineare Gleichungssysteme lösen? Es gibt eine Unzahl an Algorithmen für dieses Problem, die fast keine Wünsche (bis auf die mathematisch unmöglichen) offenlassen. Wenn man sich die Lösungsstrategien anschaut, kann man aber noch etwas wichtiges über die Struktur von linearen Abbildungen und den damit verbundenen LGS lernen.
Wir kennen bereits aus der Schule und den Grundvorlesungen verschiedene algebraische Lösungsverfahren. Relativ einfach zu programmieren ist das Gaußsche Eliminationsverfahren: Hier wendet man Zeilentransformationen auf \(\mathbf{M}\) und \(\mathbf{y}\) so lange an, bis eine obere Dreiecksmatrix entsteht, und setzt dann nach und nach Rückwärts wieder ein. Man kann dieses Verfahren auch auf singuläre Systeme mit \(\operatorname{rang}(\mathbf{M}) < \dim (V_1)\) anwenden - dann entstehen größere Treppenstufen in dem Dreieck (man verliert Zeilen) und man sieht so die invarianten Unterräume, die den Kern aufspannen.
Man kann auch das Inverse einer Matrix mit Gausselimination bestimmen, indem man den Algorithmus simultan auf alle Spalten der Einheitsmatrix anwendet.
Für die Details sei auf die Literatur verwiesen.
Das Gaussverfahren ist nur für relativ kleine Matrizen geeignet. Für größere \(\mathbf{M}\) ist erstmal der kubische Aufwand (\(\mathcal{O}(n^3)\) für \(n \times n\) Matrizen) eine Hürde; noch schlimmer ist aber wahrscheinlich, dass sich Fehler immer weiter aufaddieren, und man nach der letzten der \(n^3\) Operationen nicht mehr viel sinnvolles erhält (wenn \(n\) ordentlich groß ist). Besser geeignet sind daher iterative Verfahren, die die Lösung in jedem Schritt etwas verbessern, indem sie den Fehler \((\mathbf{M}\mathbf{x} - \mathbf{y})\) immer wieder ein bischen dämpfen. Hier gibt es verschiedene Standardstrategien:
Alle diese Verfahren lohnen sich insbesondere dann, wenn die Matrizen dünn-besetzt sind, also fast nur aus Nullen bestehen. Dies ist sehr häufig der Fall, da dies fast immer bei der Lösung partieller Differentialgleichungen auftritt, und die machen einen großen Teil des Bedarfs aus.
Weitere Details zu alle dem gehen über den Stoff der Vorlesung hinaus. Wer mehr lernen möchte, dem sei das Papier “An Introduction to the Conjugate Gradient Method without the Agonizing Pain” von J.R. Shewchuck empfohlen (von 1994), der dieses aus Frust über die unanschauliche Darstellung in vielen Lehrbüchern der damaligen Zeit geschrieben hat. Hier lernt man sehr viel über iterative LGS-Löser, ohne in Formelwüsten zu versinken.
Ein wichtiges Werkzeug, sowohl für die praktische Numerik, wie auch für die theoretische Analyse linearer Probleme ist die Matrixfaktorisierung. Dabei stellt man eine Matrix \(\mathbf{M}\), die noch irgendwie “kompliziert” ist, als Produkt von “einfachen” Matrizen dar. Und dann versteht man die Problemstruktur aufeinmal viel besser.
Was auf den ersten Blick wieder wie mentale Gymnastikübungen zum Selbstzweck aussehen mag, ist in der Tat aber ausgesprochen nützlich. <Übertreibung> Insbesondere eine spezielle Matrixfaktorisierung in Eigen- bzw. Singulärbasen ist wahrscheinlich der einzige “neue” Trick den man in dieser Veranstaltung lernt, und damit kann man große Teile der modernen Ingenieurswissenschaften erschlagen (den Trick zu kennen unterscheidet die Schulbildung von der Universitären Ingenieursbildung) </Übertreibung>.
Back to Gauss: Die LR-Zerlegung
Als Beispiel schauen wir uns nochmal den Gaussalgorithmus an. Man kann diesen leicht modifizieren, so dass er als Ausgabe eine Matrix \(\mathbf{M}\) in eine linke obere und rechte untere Dreiecksmatrix zerlegt:
\[ \mathbf{M} = \mathbf{L} \mathbf{R} \]
Sobald man diese Zerlegung kennt, kann man die Lösung von
\[ \mathbf{M}\mathbf{x} = \mathbf{y} \] also \[ \mathbf{L}\mathbf{R}\mathbf{x} = \mathbf{y} \] ganz einfach ausrechnen. Bei einer Dreiecksmatrix kann man durch iterative Substitution (angefangen an der Zeile, die nur einen Eintrag hat) direkt die Lösung ausrechnen. Das macht man hier zweimal nacheinander.
Wenn man ein LGS für mehrere rechte Seiten lösen muss, lohnt sich die LR-Zerlegung gegenüber dem einfachen Gaussalgorithmus (und ist numerisch etwas genauer als die Matrixinvertierung).
Das ganze soll aber nur als einleitendes Beispiel dienen. Wesentlich cooler sind die Faktorisierungen mit orthogonalen Matrizen. Los geht’s.
Orthogonale Matrizen
Aufgepaßt: Eine Matrix heißt “orthogonal”, falls die Spalten der Matrix ortho-normal sind, also senkrecht aufeinander stehen, und die Länge \(1\) haben. Warum man dazu nicht “orthonomale Matrix” sagt, erschließt sich mir nicht (es ist so üblich, aber ein großer Quell an Verwirrung).
Nun gut, was heißt das? Zunächst nochmal die formale Definition:
\[ \mathbf{M} = \left( \begin{array}{ccc} | & & | \\ \mathbf{m}_1 & \cdots & \mathbf{m}_d \\ | & & | \end{array} \right) = \text{ ist orthogonal} :\Leftrightarrow \forall i,j \in \{1...d\}: \langle m_i, m_j \rangle = \delta_{i,j} \]
Es ist relativ einfach zu zeigen, dass - Die Zeilen einer orthogonalen Matrix ebenfalls orthonormal sind. - Das eine orthogonale \(d \times d\) Matrix immer invertierbar ist. - Das eine orthogonale Matrix eine Drehung und/oder Spiegelung darstellt (es ist eine reine Drehung genau dann, wenn \(\det(\mathbf{M}) = 1\), und nicht \(=-1\), was die einzige andere Option ist). - Das inverse einer orthogonalen Matrix \(\mathbf{M}\) ist ihre Transponierte \(\mathbf{M}^T\) (also die Matrix, bei der man Zeilen und Spalten vertauscht hat): \[ \text{Für orthogonale }\mathbf{M}\text{ gilt: } \mathbf{M}^{-1} = \mathbf{M}^T \] Der Beweis ist super-einfach (und nützlich zu sehen, um spätere Ergebnisse zu verstehen): \[\mathbf{M}^T \cdot \mathbf{M} = \left( \begin{array}{ccc} - & \mathbf{m}_1 & - \\ & \vdots & \\ - & \mathbf{m}_d & - \end{array} \right) \cdot \left( \begin{array}{ccc} | & & | \\ \mathbf{m}_1 & \cdots & \mathbf{m}_d \\ | & & | \end{array} \right) = \left( \begin{array}{ccc} \langle \mathbf{m}_1, \mathbf{m}_1 \rangle & \cdots & \langle \mathbf{m}_1, \mathbf{m}_d \rangle \\ \vdots & \ddots & \vdots \\ \langle \mathbf{m}_d, \mathbf{m}_1 \rangle & \cdots & \langle \mathbf{m}_d, \mathbf{m}_d \rangle \end{array} \right) = \mathbf{I} \]
Orthogonale Transformationen sind numerisch besonders stabil: Sie ändern die Länge von Vektoren nicht, so dass man nicht Zahlen sehr unterschiedlicher Größenordnung verrechnen muss, was eine wesentliche Quelle für Genauigkeitsprobleme bei Fließkommaarithmetik ist. Entsprechend kann man versuchen, damit LGS zu lösen:
Man kann jede Matrix \(\mathbf{M} \in \mathbb{R}^{n \times m}\) in eine orthognoale \(m \times m\)-Matrix \(\mathbf{Q}\) und eine rechte-obere Dreiecksmatrix \(\mathbf{R}\) zerlegen: \[ \mathbf{M} = \mathbf{Q} \mathbf{R} \] Der konstruktive Beweis liefert einen einfachen Algorithmus für dieses Problem, der relativ leicht zu verstehen ist (die “Householder-methode”). Wir skizzieren hier nur die grobe Idee: Nehmen wir (vereinfachend) an, dass \(\mathbf{M}\) quadratisch und invertierbar ist. Dann könnenw wir die erste Spalte der Matrix mit einer Dreh- oder Spiegelmatrix (Herr Householder nimmter letztere) so transformieren, dass er auf die x-Achse fällt. Die Matrix, die übrig bleibt, hat nun nur noch einen Eintrag (in x) und sonst nur noch Nullen. Danach machen wir das nochmal, und versuchen die zweite Spalte zu kippen. Es gelingt im Allgemeinen nicht, die Spalte auf die y-Achse zu kippen, da sie nicht senkrecht auf der ersten Spalte stehen muß, und Drehungen bzw. Spiegelungen Winkel erhalten. Naja, dann bringen wir sie in die xy-Ebene. Und die dritte Spalte in die xyz-Hyperebene, und so weiter. Am Ende steht ein Produkt von Spiegelungen oder Drehmatrizen und einer Dreiecksmatrix. Voilà.
Was bringt es?
Man kann mit der Zerlegung wieder direkt das LGS lösen: Die \(\mathbf{R}\)-Matrix nutzt man, um die rechte Seite zurückzusubstituieren, und das Ergebnis multipliziert man mit dem Inversen von \(\mathbf{Q}\). Freundlicherweise ist das \(\mathbf{Q}^T\). Und \(\mathbf{Q}^T\) aus \(\mathbf{Q}\) auszurechnen, ist eine Übungsaufgabe aus den ersten Stunden von Einführung in die Programmierung. Nett ist auch, dass dieser Algorithmus viel genauer als die Gauselimination oder LR-Zerlegung ist, da nur orthogonale Transformationen benutzt werden, die jeweils viel weniger numerische Fehler anhäufen. Man kann die Transformation so auch so implementieren, dass sie, wei Gauss, in \(\mathcal{O}(n^3)\) Zeit abläuft. Im Prinzip ist das Ding also mehr oder weniger grundsätzlich zu bevorzugen.
Die Zerlegung hat noch viele andere Anwendungen (Eigenwertberechnung, Pseudo-Inverse, etc.). Siehe dazu z.B. den Wikipediaartikel zum Thema.
Eigenwerte sind eine auf den ersten (vielleicht auch zweiten) Blick obskure Idee aus der linearen Algebra, die sich aber am Ende als ungemein praktisch darstellt. Schauen wir uns nochmal die Definition an:
Eine lineare Abbildung \(f:V_1 \rightarrow V_2\) hat einen Eigenwert \(\lambda\) zu einem Eigenvektor \(\mathbf{v}\) genau dann, wenn
\[ f(\mathbf{v}) = \lambda \cdot \mathbf{v} \]
Das ganze geht auch ganz genauso im Spezialfall der Matrizen (\(\mathbf{M} \mathbf{v} = \lambda \mathbf{v}\)).
Für manche - aber nicht alle - Matrizen (bzw. linearen Abbildungen) kann man eine Eigenbasis finden, also eine Basis, die den ganzen Raum aufspannt und nur aus Eigenvektoren besteht. Wenn dies gelingt, dann kann man die Abbildung damit diagonalisieren. Wir schauen uns erstmal den Matrixfall an:
Sei \(\mathbf{M} \in \mathbb{R}^{d \times d}\) und seien \(\{\mathbf{u}_1,...\mathbf{u}_d\}\) lineare unabhängige Eigenvektoren (die damit eine Eigenbasis bilden). Dann kann man \(\mathbf{M}\) wie folgt faktorisieren:
\[ \mathbf{M} = \mathbf{U} \mathbf{D} \mathbf{U}^{-1} \] mit \[ \mathbf{D} = \left( \begin{array}{ccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & & \vdots\\ \vdots & & \ddots & 0\\ 0 & \cdots & 0 & \lambda_d \end{array} \right) \]
Besonders interessant ist der Fall symmetrischer Matrizen (die uns später, im least-squares und Varitionsrechnungskapitel dauernd über den Weg laufen). Für reelle symmetrische Matrizen, also \(\mathbf{M} \in \mathbb{R}^{d \times d}\) mit \(\mathbf{M} = \mathbf{M}^T\) gilt, dass Sie immer eine vollständige Eigenbasis haben, die zusätzlich auch noch orthogonal ist (also alle senkrecht aufeinander stehen; die Länge eins kann man ohne Probleme wählen, da alle vielfachen von Eigenvektoren wieder Eigenvektoren sind). In dem Fall vereinfacht sich die Faktorisierung zu:
\[ \mathbf{M} = \mathbf{U} \mathbf{D} \mathbf{U}^{T} \]
Der Unterschied ist das kleine T: Statt Invertieren braucht man hier nur transponieren, was sich natürlich sehr leicht berechnen läßt. Kennt man also die Eigenwerte und Eigenvektoren einer symmetrischen Matrix, dann kann man lineare Gleichungssysteme leicht lösen. Diese zu berechnen ist aber nicht unbedingt einfacher - man kann hier die QR-Zerlegung, oder die SVD benutzen; für manche, sehr große Probleme, gibt es auch iterativer Verfahren, wie die Power-Iteration (siehe Vorlesungsfolien; dort wird auch erklärt, wie man Potenzen von symmetrischen Matrizen einfach die Eigenzerlegungen bestimmen kann).
Die QR-Zerlegung kann man noch etwas hübscher machen, indem man die (unhandliche) Dreiecksmatrix ebenfalls durch eine orthogonale Matrix ersetzt. Man erhält die folgende Zerlegung:
Singulärwertzerlegung (Singular Value Decomposition, SVD): Sei \(\mathbf{M} \in \mathbb{R}^{n \times m}\). Dann kann man \(\mathbf{M}\) immer schreiben als Produkt einer orthogonalen, einer diagonalen und einer weiteren orthogonalen Matrix, wie folgt:
\[\begin{eqnarray} \mathbf{M} &=& \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T \\ &=& \left( \begin{array}{ccc} |& & |\\ \mathbf{u}_1& \cdots & \mathbf{u}_m \\ |& &| \end{array} \right) \cdot \left( \begin{array}{cccc|cc} \sigma_1 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 &\sigma_2& & \vdots & \vdots & & \vdots \\ \vdots & & \ddots & 0 & \vdots & & \vdots \\ 0 & \cdots & 0 & \sigma_d & 0 & \cdots & 0 \\ \hline 0 & \cdots & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & & & \vdots & \vdots & & \vdots \\ 0 & \cdots & \cdots & 0 & 0 & \cdots & 0 \end{array} \right) \cdot \left( \begin{array}{ccc}-& \mathbf{v}_1 & -\\ & \vdots & \\-& \mathbf{v}_n &- \end{array} \right) \end{eqnarray}\]
Die Diagonalmatrix ist dabei für \(n \neq m\) rechteckig, aber außerhalb der oberen linken \(d\times d\)-Matrix (für \(d=\min(n,m)\)) nur mit Nullen gefüllt.
Die Berechnung kann man ähnlich wie die QR-Zerlegung beginnen; der zweite Schritt, die R-Matrix zu diagonalisieren, ist aber anders.
Eine wirklich sehr schön Erklärung, mit anschaulichen Animationen liefert Wikipedia (falls niemand seit August 2020 die Seite verunstaltet hat).
Die Vektoren \(\mathbf{u}_i\) heißen linksseitige und die \(\mathbf{v}_i\) rechtsseitige Singulärvektoren, und die \(\sigma_i\) hören in aller Regel auf den Namen Singulärwerte. Die Schreibweise mit \(\mathbf{V}^T\) ist üblich als Konvention (dann sind immer die Spalten die Singulärvektoren, und man sieht vielleicht eher, das man in das Koordinatensytem von \(\mathbf{V}\) wechselt und aus dem von \(\mathbf{U}\) wieder heraus - einen über die Ästhetik hinausgehenden, tieferen Sinn hat es wohl nicht).
Was kann man damit machen?
Und noch vieles mehr. Was uns besonders interessiert, ist zu verstehen, wie “invertierbar” ein lineares Problem in der Praxis ist. Dazu mehr im nächsten Unterabschnitt. Zuvor noch kurz eine Bemerkung zur Theorie.
Die SVD für Funktionenräume
Man kann die Idee der Singulärwertzerlegung auch auf Funktionenräume anwenden. Hier gibt es, wie üblich, einige technische Probleme zu beachten (die wir mal wieder unter den Tisch fallen lassen). Die Grundidee ist, anzunehmen, dass es eine Schauderbasis für das ganze Ding (den Eingabe-Funktionenraum und den Ausgabe-Funktionenraum) gibt (wie z.B. die Fourier-Basis für \(L_2[0,2\pi]\)). Dann würde man die SVD als Reihenentwicklung schreiben, ähnlich wie wir es schon in Kapitel 2.3 gesehen hatten: Für einen linearen Operator \(M\) erhalten wir die Darstellung
\[ Mf = \sum_{i=1}^\infty \left( \sum_{j=1}^\infty m_{i,j} \langle f, v_i \rangle \right) \cdot u_j \]
Dabei sind \((u_i)_{i\in \mathbf{N}}\) und \((v_i)_{i\in \mathbf{N}}\) jeweils folgen von orthogonalen Funktionen (also abstrakte Vektoren in unserem Funktionenraum), die eine Schauderbasis für den gesamten Eingabe- und Ausgaberaum darstellen, und \((\sigma_i)_{i\in \mathbf{N}}\) eine unendliche Folge von Singulärwerten.
Für beschränkte lineare Operatoren (was ungefähr heißt, dass die \(\sigma_i\) nicht unendlich groß werden können), und unter noch ein paar anderen technischen Bedingungen, existiert dann auch eine kontinuierliche SVD, die die Struktur der Abbildung vielleicht besser erklärt.
In der Praxis rechnen wir dann doch immer mit der Matrix-SVD und einer geeigneten Diskretisierung. Von daher nichts für ungut (und wenn doch, hilft eine Vorlesung in Funktionalanalysis).
Diagonalisierung für Funktionenräume Die Eigenwertzerlegung kann man ähnlich darstellen: Hier ist \(u_i=v_i\), falls die Abbildung “symmetrisch” ist, was man im unendlich-dimensionalen selbstadjungiert nennt\(^{*)}\).
\(^*)\) Selbstadjungiert: Die Symmetrie von linearen Operatoren auf Funktionenräume ist wieder indirekt definiert, über das Skalarprodukt: Es muss \(\langle M f, g\rangle = \langle f, M g\rangle\) für alle Funktionen \(f,g\) gelten; wenn man sich hier eine (Schauder-)Basis eingesetzt denkt, bekommt man die Einträge der Matrizendarstellung und ihrer Transponierten, die symmetrisch sein sollen.
Für Eigenfunktionen gibt es ein paar hübsche Beispiele: Nimmt man z.B. den Funktionenraum \(L_2[0,2\pi]\) von komplex-wertigen Funktionen \[ f:[0,2\pi] \rightarrow \mathbb{C}, \] definiert auf einem Intervall (jedes Intervall geht; für \([0,2\pi]\) hat man am wenigsten Schreibarbeit), so kann man eine Fourierbasis als Schauderbasis benutzen, um jede Funktion darzustellen (im Sinne das die Reihenapproximation einen Fehler läßt, der Norm Null in Bezug auf das Skalarprodukt hat): \[ B = \{e^{-ikx} | k\in \mathbb{Z}\} \] Dann sieht man ohne Umwege, dass die Ableitung (die eine lineare Abbildung auf dem Funktionenraum ist), die Fourier-Basisfunktionen als Eigenfunktionen hat, mit Eigenwert \(k\). Insbesondere heißt dass, dass die Ableitung auf hohe Frequenzen immer stärker (unbeschränkt stark) reagiert.
Cool. Aber wofür soll so eine Einsicht gut sein?
Wir betrachten nun sogenannte “inverse Probleme”. Ein inverses Problem ist nichts anderes, als die Gleichung \(f(x)=y\) für bekanntes \(f\) und \(y\) nach \(x\) aufzulösen. Dabei ist \(f\) in der regel ein natürlicher Vorgang, den wir modelliert haben, und bei dem wir \(y\) messen können. Das \(f\) modelliert dabei die Eigenschaften und Einschränkungen des Messvorgangs mit. Wenn \(f\) eine lineare Abbildung ist, dann können wir mit der Singulärwertzerlegung die Sache besser verstehen:
Stellen wir uns also vor, wir haben eine Matrix \(\mathbf{M}\), eine Ergebnis \(\mathbf{y}\) und möchten die Gleichung \(\mathbf{M}\mathbf{x}=\mathbf{y}\) nach \(\mathbf{x}\) auflösen. Dabei müssen wir davon ausgehen, dass wir \(\mathbf{y}\) nicht beliebig genau kennen, da es wahrscheinlich aus einem Messgerät stammt, und jede echte physikalische Messung hat eine gewisse Ungenauigkeit (meist in der Form von zufälligem Rauschen). Der Fehler ist vielleicht auch nicht ganz unerheblich, da wir nicht genug Budget für ein super-gutes Messgerät hatten (oder das Problem super-schwierig ist, so dass man es nicht einfach mit Geld lösen kann).
Ok - so what could possibly go wrong?
Wir müssen im Prinzip \(\mathbf{x} = \mathbf{M}^{-1}\mathbf{y}\) rechnen. Wenn wir die Matrix \(\mathbf{M}\) in der Singulärwertzerlegung schreiben, dann erhalten wir (wir nehmen eine quadratische Matrix an, damit es nicht zu unübersichtlich wird):
\[ \mathbf{M}^{-1} = \mathbf{V} \cdot \mathbf{\Sigma}^{-1} \cdot \mathbf{U}^T = \mathbf{V} \cdot \left( \begin{array}{cccc} \sigma_1^{-1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_d^{-1} \end{array} \right) \cdot \mathbf{U}^T \]
Die orthogonalen Matrizen machen hier nichts - sie verstärken keine Fehler, da sie die Norm des Eingabevektors \(\mathbf{y}\) nicht ändern. Der Mörder ist die Diagonalmatrix (wie immer): wenn die Singulärwerte (betragsmäßig) sehr klein sind, dann verstärken sich die Fehler sehr stark. Sollte der Betrag kleiner als das Messrauschen in \(\mathbf{y}\) sein, so erhält man eine starke Verstärkung von diesem Rauschen, und das Endergebnis ist völlig unbrauchbar (aufwendiger Zufallszahlengenerator mit großen Ausgabenwerten, falls mindestens einder der \(|\sigma_i|\) sehr klein wird).
Was tun? - Wir müssen uns klar machen, dass eine matrix praktisch nicht invertierbar ist, wenn einzelne Singulärwerte unter dem Rauschniveau liegen. - Wir können versuchen, zu retten was zu retten ist: Wir invertieren nicht alles, sondern lassen die Unterräume, in denen \(|\sigma_i|\) zu klein ist einfach weg. In der oben gezeigten SVD-Inversen setzen wir dann einfach eine \(0\) statt \(\sigma_i^{-1}\) ein. - Techniken, die so etwas machen, nennt man Regularisierung (die SVD-Methode ist eine einfache Regularisierungstechnik, aber nicht die einzige).
Die Inverse, die man erhält wenn man betragskleine \(\sigma_i\) wegläßt (im Original, solche, die null sind), nennt man die Pseudoinverse, bezeichnet mit \(\mathbf{M}^\dagger\). Das Kreuz deutet an, dass hier vielleicht schon einige Informationen gestorben sind…
Probleme, bei denen die Singulärwerte sehr klein werden (oder es gar keine eindeutige, oder auch wirklich gar keine Lösung gibt), bei denen also die die Singulärwerte der Inversen zu groß werden, und das Rauschen über das Signalniveau heben können, heißen auch schlecht gestellte Probleme (ill-posed Problems).
Die theoretische Definition ist noch etwas abstrakter, und kann auch auf unendlich-dimensionale Funktionenräume angewandt werden. Ein konkretes Beispiel hierfür ist das Problem, eine Ableitung zu bestimmen. Wie wir gerade zuvor gesehen haben, divergieren die Eigenwerte (was hier die Singulärwerte wären) - sie werden für hoch-frequente Eingabefunktionen unendlich groß (wachsen linear mit der Frequenz). Daher ist Ableiten ein schlecht gestelltes Problem. Man merkt das auch: Wenn man etwas Rauschen auf dem Messsignal hat, und dann den Differenzenquotienten von benachbarten Werten bildet, verstärkt man das Rauschen erheblich. Eine Lösung ist, die Funktion vor dem Ableiten mit einem Tiefpassfilter (z.B. Mittelwert über \(k\) Messwerte) zu behandeln; dann klappt das schon viel besser.
Beispiele: Es gibt eine ganze Reihe von Beispielen von linearen inversen Problemen, die in der Praxis relevant sind: - Computertomographie: Die Aufgabe besteht darin, aus Linienintegralen (Summen entlang von Strahlen), die integrierten Werte zu rekonstruieren. Das Problem hat ein (moderat) abfallendes Singulärwertspektrum, was eine Regularisierung beim Lösen des LGS nötig macht. - Bildrekonstruktion: Wir haben ein unscharfes Bild gemacht (vielleicht war die Optik schlecht) - können wir das wieder schärfen? Dies ist leider sehr ill-posed (das Spektrum fällt exponentiell im quadrat mit der Frequenz ab - da kann man nicht sehr viel machen. Herleitung in Kapitel 6). - Bestimmung der Steigerungsraten aus Zeitreihen: Auch bekannt als Ableitung. Im Rahmen der COVID19-Pandemie hat sich dies auch als ein Problem herausgestellt, und das Ableitungen ill-posed sind, macht die Sache nicht einfacher.
Aufgabe 2.1: Affine Abbildungen. Leiten Sie eine Formel her, mit der man Punkte im \(d\)-Dimensionalen Raum um eine beliebige Achse drehen kann, die durch die Geradengleichung \(\mathbf{p}(t) = \mathbf{m}t +\mathbf{n}\) dargestellt ist. Der Winkel soll \(\alpha\) betragen.
Aufgabe 2.2: Abstrakte lineare Abbildungen. Zeigen Sie, dass die Menge aller Funktionen, die spiegelsymmetrisch um die \(y\)-Achse sind, ein linearer Unterraum der Menge aller Funktionen \(f: \mathbb{R} \rightarrow \mathbb{R}\) ist.
Aufgabe 2.3: Matrixfaktorisierung. Beweisen Sie, das die linksseitigen Singulärvektoren einer (beliebigen) reellen Matrix \(\mathbf{M}\) die Eigenvektoren der Matrix \(\mathbf{M}\mathbf{M}^T\) sind. Zeigen Sie (mit fast den gleichen Argumenten), dass die rechtsseitigen Singulärvektoren den Eigenvektoren von \(\mathbf{M}^T\mathbf{M}\) entsprechen. Was passiert jeweils mit den Eigenwerten? Vergessen Sie nicht, zu erklären, warum die überhaupt alle existieren.
Aufgabe 2.4: Inverse Probleme - Tikhonov-Regularisierung. Sei \(\mathbf{M}\mathbf{x}=\mathbf{y}\) ein schlecht gestelltes Problem. Erklären Sie anschaulich, warum es nicht weniger problematisch, sondern eher mehr, ist, das Optimierungsproblem \[||\mathbf{M}\mathbf{x}-\mathbf{y}||^2 \rightarrow \min\] zu lösen. Dagegen hilft es, das Problem umzuformulieren als \[||(\mathbf{M}+\lambda \mathbf{I})\mathbf{x}-\mathbf{y}||^2 \rightarrow \min,\] mit einem geeignet gewählten Regularisierungsparameter \(\lambda>0\). Warum ist das besser, und wie sollte man \(\lambda\) ungefähr wählen, damit es hilft?
Aufgabe 2.5: Inverse Probleme - Tikhonov-Regularisierung, Teil 2. Das ganze ist auch in einer Variante bekannt, bei der man funktionale Optimierungprobleme \(Mf=g\) (gesucht ist, vgl. Kapitel 7 - Variationsrechnung) regularisiert, indem man ansetzt: \[ ||Mf-g||^2 + \lambda \left\lVert\frac{d}{dx} f\right\rVert^2 \rightarrow \min \] Was steckt hier dahinter? Man benutzt das auch mit höheren Ableitungen (vgl. Übungsaufgabe zur Bildrekonstruktion).
Wir schauen uns nochmal ein paar Konzepte aus der Analysis an. Diese brauchen wir vor allem, um funktionale Gleichungen aufzustellen, also Gleichungen, die Funktionen als Unbekannte haben. Solche Gleichungen (vor allem Differential- und Integralgleichungen) sind ein zentrales Werkzeug zur Modellierung natürlicher Phänomene. Ein großer Teil der Modelle in den Naturwissenschaften beruht auf solchen Gleichugnen.
Der Begriff von Ableitung und Integration sollte aus der Schule und den Grundvorlesungen hinreichend bekannt sein. Hier nochmal die 1-Slide-Summary zur Erinnerung:
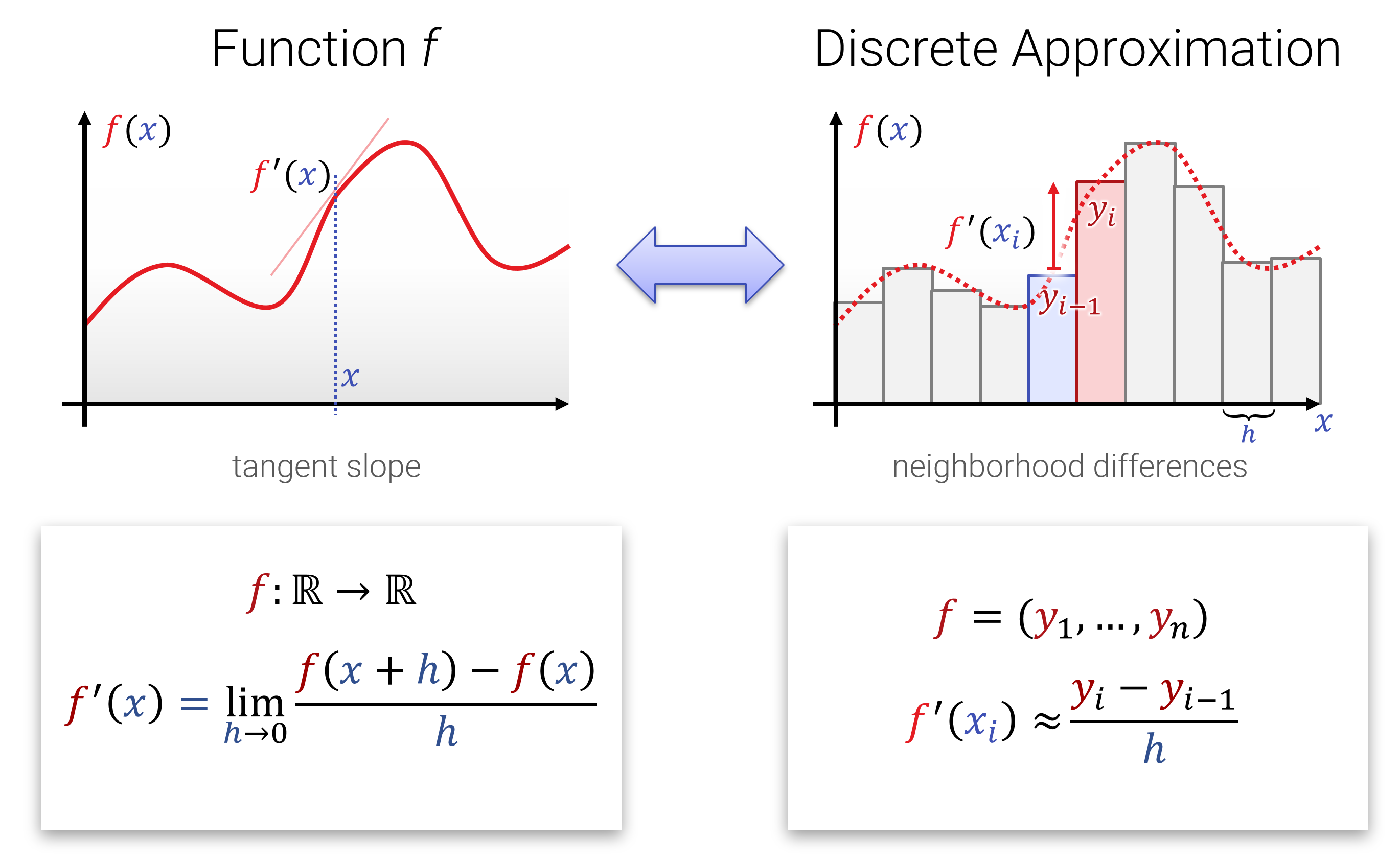
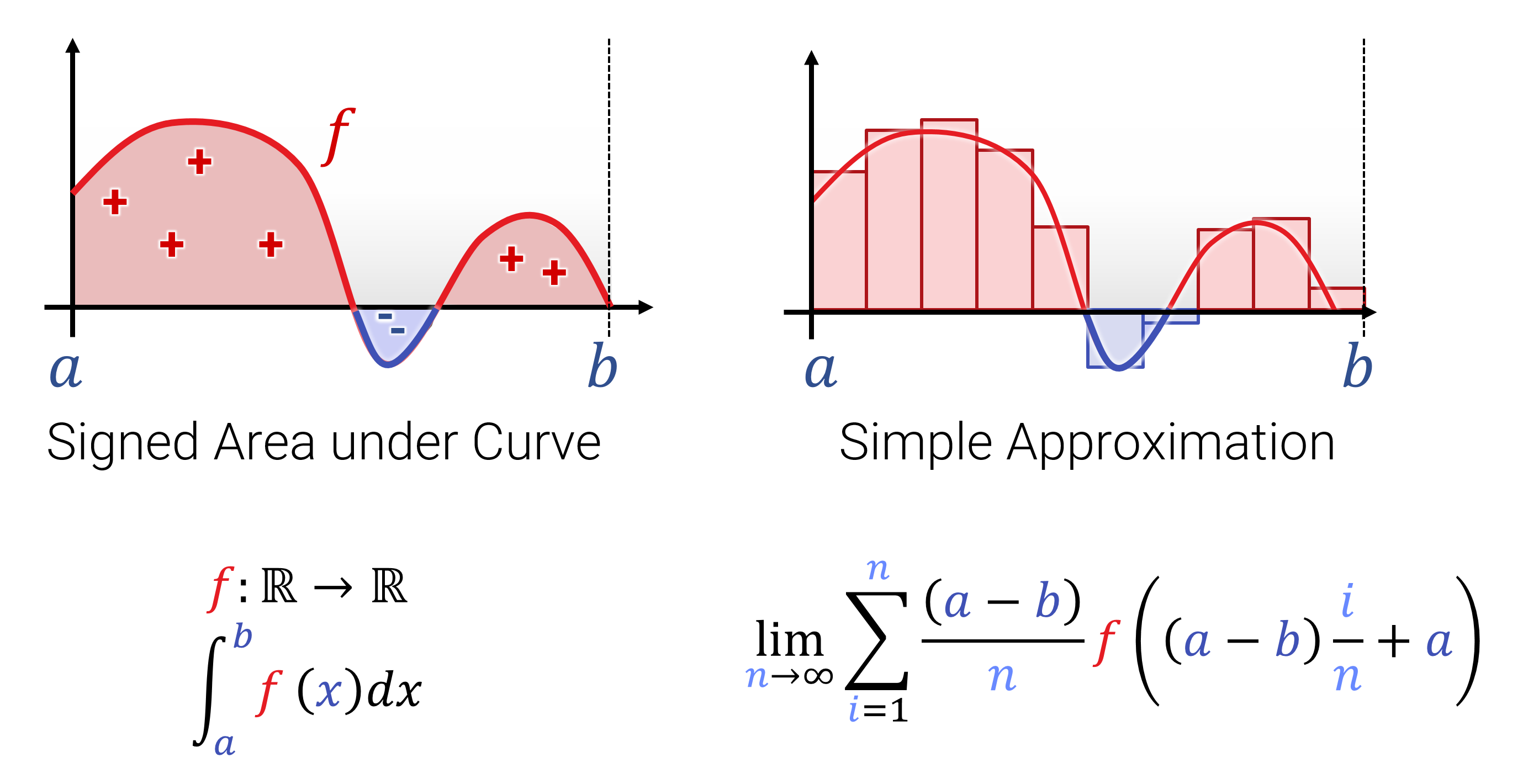
Ableitungen kann man auch im Mehrdimensionalen bilden; hierzu werden bei einer Funktion \[ f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} \] einfache alle Ableitungen von allen \(m\) Ausgaben in alle \(n\) Eingaberichtungen gebildet. Das Ergebnis bezeichnet man als \(\nabla f\). Je nach Dimension erhält man einen Zeilen- oder Spaltenvektor, oder auch eine ganze Matrix (dann spricht man auch von der Jacobi-Matrix \(J_f\)).
Man schreibt den Ableitungsoperator nach einer Koordinate \(x_i\) nun nicht mehr als \(\frac{d}{dx}\) sondern als \(\frac{\partial}{\partial_{x_i}}\) oder auch \(\partial_{x_i}\). Bis auf die Krümmung im \(d\) ändert sich gar nichts.
Das ganze (gemeint ist die Ableitung, nicht die Krümmung des \(d\)) kann man beliebig oft wiederholen - man erhält dann Tensoren (also mehrdimensionale Array von Ableitungen) von Ableitungen hoherer Ordnung in Kombinationen von verschiedenen Richtungen, und für alle Ausgaben (siehe Vorlesungsfolien für eine genauere Diskussion, warum dies “Tensoren” und nicht einfach nur Arrays sind, bzw. was das eigentlich heißt.)
Entscheident für das Verständnis von Ableitungen ist der Satz von Taylor, dass eine Funktion, die \(k\)-mal stetig differenzierbar (d.h., die k-te Ableitung ist möglich und das Ergebnis ist immer noch stetig) ist, durch ein Polynom \(k\)-ter Ordnung in einer kleinen Umgebung um den abgeleiteten Punkt beliebig genau angenähert werden kann.
Das bedeutet, man kann mit Hilfe von Ableitungen glatte Funktionen lokal durch Polynome annähern kann. Das ist cool, weil die viel einfacher und oft leichter zu analysieren sind als die Originalfunktionen (bei denen es sich in schlimmeren Fällen z.B. um Messwerte ohne analytische Formel handeln könnte).
Für 1D lautet die Formel von Taylor:
\[ f(x) \approx f(x_0)+\sum_{k=1}^n \frac{1}{k!}\frac{d^k}{dx^k}f(x_0)\cdot (x-x_0)^k \]
Wenn die Funktion aus \(C^n\) stammt (\(n\)-mal stetig differenzierbar), dann existiert für jede Abweichung \(\delta>0\) eine Umgebung \(\epsilon>0\) um \(x_0\), in der der Approximationsfehler nicht größer als \(\delta\) wird.
Im Mehrdimensionalen gilt das gleiche, nur die Formal sieht furchbar aus (für unerschrockene: siehe Vorlesungsfolien).
Hier zwei Beispiele für Approximationen eines Höhenfeldes \(f:\mathbb{R}^2 \rightarrow \mathbb{R}\) mit Polynomen erster und zweiter Ordnung:
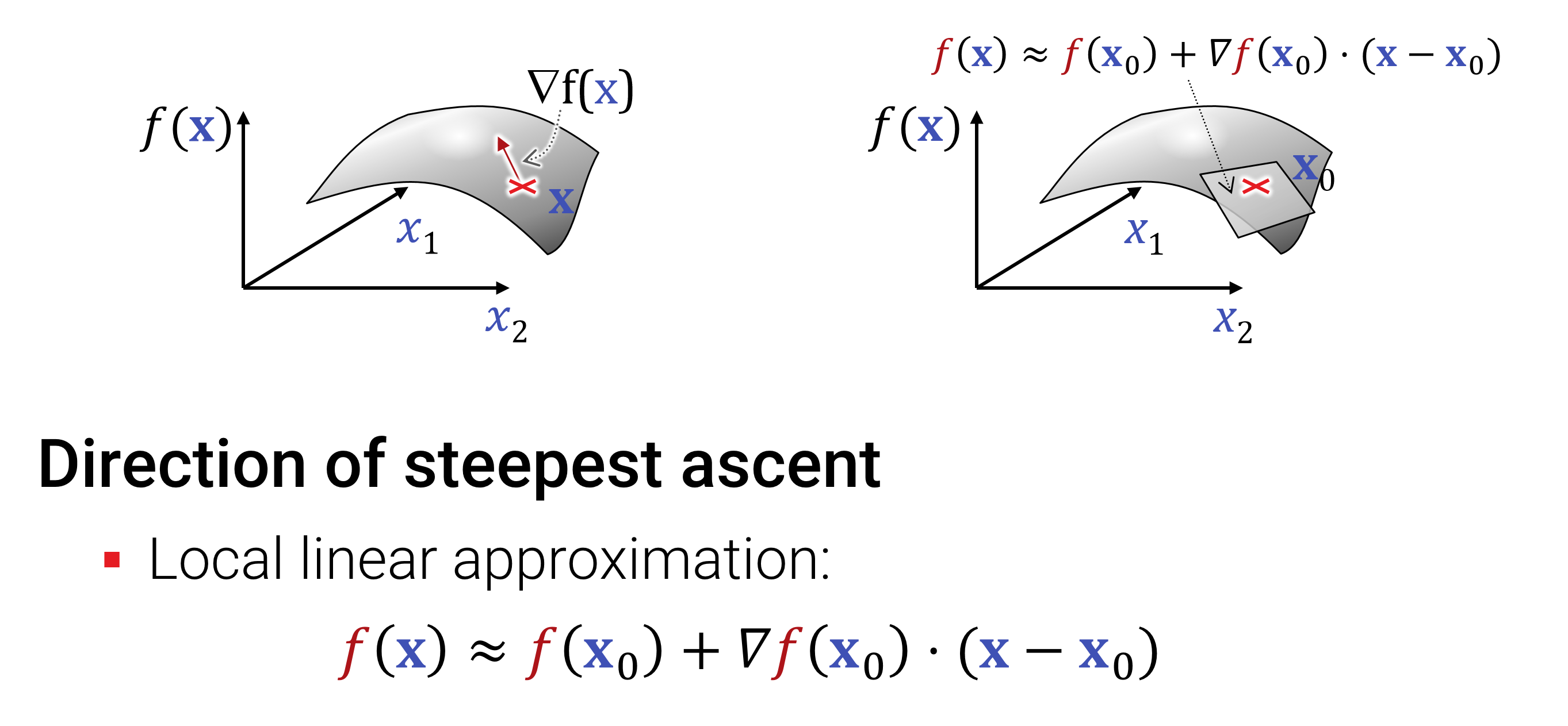
![Abbildung: Die Annäherung kann man auch zweiter Ordnung machen. Dabei ist \mathbf{H}_f = [\partial_{x_i}\partial_{x_j} f]_{i,j \in {1,..,d}} die Matrix aller zweiten Ableitungen, genannt Hessematrix.](images/wdh/taylor-2nd-order-manifold.png)
Wir möchten nun Gleichungssysteme aufstellen, die Funktionen als Lösung haben. Das ist im Prinzip nichts wildes - man wendet eine Funktion höherer Ordnung (wie die Informatiker*innen sagen würden) \(F\) auf eine unbekannte Funktion \(f\) an und verlangt, das eine (nun wieder bekannte) Funktion \(g\) entsteht. \(F\), was auch gegeben ist, bildet dabei Funktionen auf Funktionen (oder Zahlen) ab. Die allgemeine Form sieht dann so aus: \[ F(f)=g \] Wenn \(F\) eine lineare Abbildung (von einem Funktionenraum in einen Funktionenraum) ist, dann nennt man \(F\) auch einen linearen Operator. Als Buchstaben bevorzugt man dann oft das \(L\), weil es so intensiv an das Wort “linear” erinner. Und weil es cooler aussieht (fast so wie eine Matrix), läßt man oft die Klammern weg: \[ L f=g \]
Die Interessantere Frage ist natürlich, welche sinnvollen/interessanten Abbildungen man den auf Funktionen loslassen kann. Dabei fallen Ableitungen und Integrale ins Auge: Das Ableiten einer Funktion, wie auch das wieder aufintegrieren sind lineare Operationen. Das sieht man sehr leicht, wenn man sich das diskretisierte Analogon anschaut (also bevor man zum Grenzwert übergegangen ist). Hier ein hübsches Bild dazu:
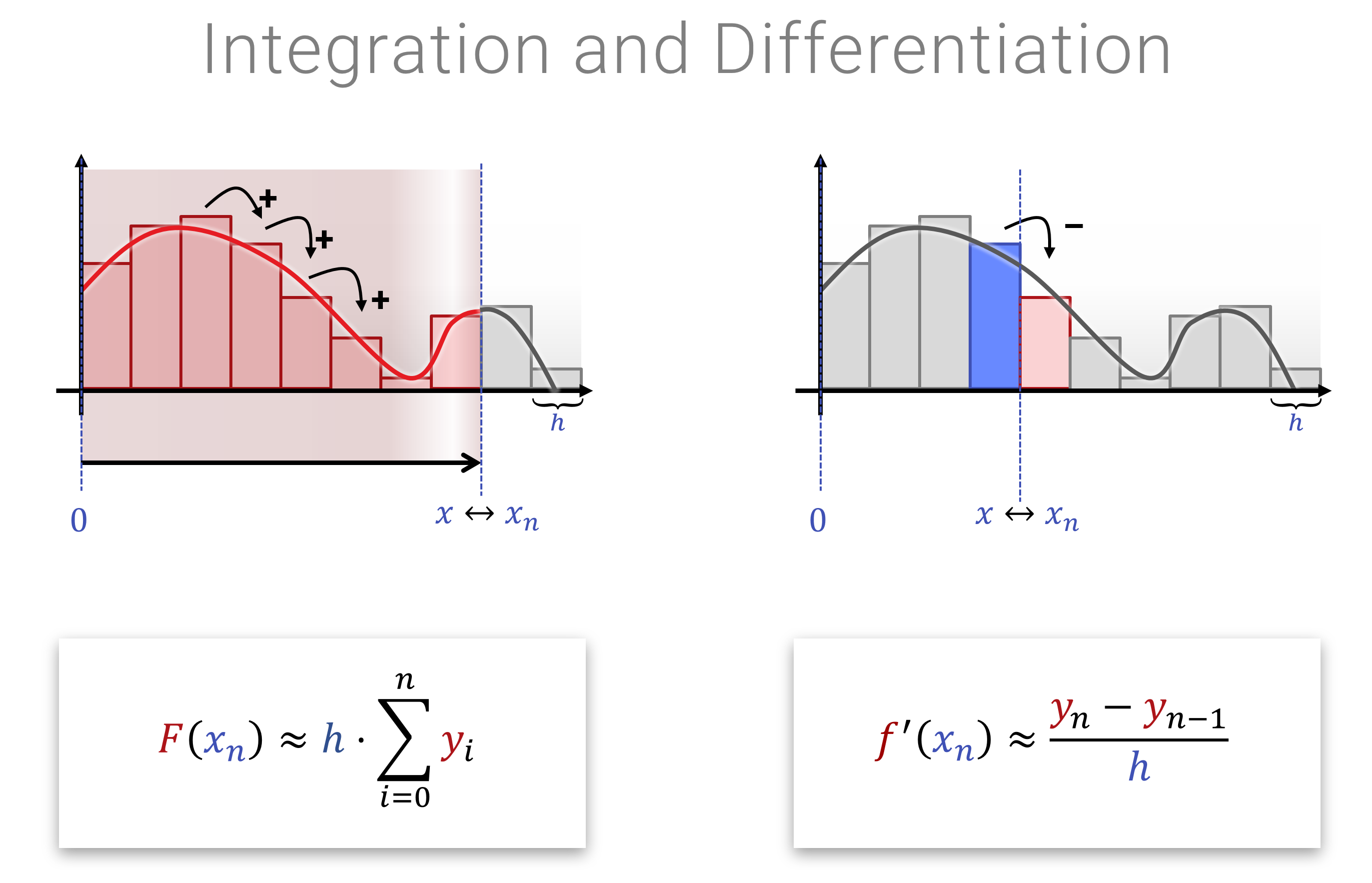
Physik: Kausalität
Physikalische Gleichungen basieren oft auf elementaren Wechselwirkungen, die mit der zeit komplexere, emergente Strukturen bilden. Wechselwirkungen sind dabei häufig räumlich und immer zeitlich lokal: Was als nächstes passiert, hängt nur vom vorangegangenen Moment ab, und oft beeinflussen räumliche Zustände zunächst nur ihre unmittelbare Nachbarsschaft. Damit erhält man, ganz natürlich, Differentialgleichung zur Beschreibung der physikalischen Phänomene. Gewöhnliche Differentialgleichungen, mit einem Zeitparameter, hat man fast immer. Partielle Differentialgleichungen bekommt man für Modelle, bei denen die Interaktionen auch räumlich lokal sind (z.B. Fluid- oder Soliddynamik, Wellengleichungen oder Quantenmechanik; letztere ist übrigens auch rein lokal, allerdings bei der Berechung der Korrelationen, nicht bei der Realisierung/Beobachtung der Ereignisse).
Gewöhnliche Differentialgleichungen (ODEs - ordinary differential equations) suchen eine vektorwertige Funktion \[ \mathbf{y} : \mathbb{R} \rightarrow \mathbb{R}^d \] \(\mathbf{y}(t)\) beschreibt dabei den Zustant zum Zeitpunkt \(t\) mit \(d\) verschiedenen Parametern, die sich über die Zeit dynamisch entwickeln: \[ \frac{d}{dt}\mathbf{y}(t) = \dot{\mathbf{y}}(t) = F(t,\mathbf{y}(t)) \] wohin die Reise als nächstes geht, hängt nur vom aktuellen Zustand ab (und kann auch von der Zeit selbst abhängen; Physikalische Gesetze selbst sind immer zeitinvariant, aber man kann per Hand zeitabhängige Vorgänge “per Hand” reinmodellieren, wie z.B. dass einer Rakete langsam der Treibstoff ausgeht). Die Gleichung ist also immer zeitlich lokal. Statt der Zeit können dies natürlich auch andere Parameter sein, aber ein \(t\) sieht man an dieser Stelle schon auffallend häufig.
Zur Lösung gibt man entweder einen Anfangswert \(\mathbf{y}(0)\) vor, oder man kann auch Zwischenwerte angeben, die erreicht werden müssen, wobei man sorgfältig darauf achten muss, dass das auch machbar ist. Auch die Simulation ist dann schwieriger.
Zur Lösung wendet man den Satz von Taylor an: In der Annahme, dass die Lösung glatt ist, nähert man sie lokal durch ein Polynom an. Dann geht man einen kleinen Zeitschritt entlang des Näherungspolynoms (welches man analytisch ausrechnen kann) und bestimmt die Approximation erneut. Die verschiedenen DGL-Solver unterscheiden sich in den meisten Fällen nur darin, wie diese Polynomextrapolation berechnet wird. Die einfachste Idee ist, eine Grade, ausgehend vom aktuellen \(\mathbf{y}(t)\) und der daraus direkt zu berechnenden Ableitung \(\dot{\mathbf{y}}(t)\) zu bestimmen, und dieser für einen kleinen Schritt \(\Delta t\) zu folgen; das nennt man dann das Eulerverfahren. Es ist weder besonders genau noch besonders stabil, aber einfach zu programmieren und verstehen, und daher dennoch ausgesprochen beliebt.
Noch eine Frage: Was macht man bei DGLs mit höheren Ableitungen? Wir ersetzen einfach \(y'' = \frac{d}{dt} y'\) und führen \(y'\) als neue Variable in unseren Zustandsvektor \(\mathbf{y}\) ein, die zusätzlich der Gleichung \(\frac{d}{dt} y = y'\) gehorcht (dabei bezeichnet das “\(\frac{d}{dt}\)” die Berechnung der Ableitungen auf der rechten Seite, und \(y,y'\) sind Variablen im Zustandvektor \(\mathbf{y}\)).
Partielle Differentialgleichungen geben Bedingungen für die partiellen Ableitungen einer Funktion an jedem Punkt der Funktion an. Wir haben hier eine unbekannte Funktion \[ \mathbf{y}: \mathbb{R}^n \rightarrow \mathbb{R}^m, \] die von mehr als einer Variablen abhängt, zusammengefaßt als \(\mathbf{x} \in \mathbb{R}^n\). Wir benutzen dann eine Gleichung der Form \[ D \mathbf{y} (\mathbf{x}, t) = F(\mathbf{y} (\mathbf{x}, t), \mathbf{x}, t), \] Dabei ist \(D\) ein Differntialoperator (Kombination von Ableitungen), und die rechte Seite schreibt vor, welchen Wert diese haben sollen (abhängig vom aktuellen Wert, sowie optional Ort und Zeit; auch hier sind elementare physikalische Gleichungen in der Regel Orts- und Zeitinvariant, aber man kann bestimmte Effekte, wie z.B. dünnere Luft weiter oben beim Start der besagten Rakete, in die Orts- oder Zeitabhängigkeit reinmodellieren).
Ein Beispiel für einen Differentialoperator ist z.B. die Summe der zweiten Ableitungen in alle Ortsrichtungen, auch bekannt als Laplaceoperator (das Ding taucht häufig auf):
\[ \text{z.B. }D = \Delta := \sum_{i=1}^n \frac{\partial^2}{\partial {x_i}^2} \] In 2D wäre dies \(D= \partial_{x_1}^2 + \partial_{x_2}^2\).
Um eine konkrete Lösung zu finden, müssen auch hier wieder zusätzliche Bedingungen vorgegeben werden. Da es im Mehrdimensionalen keinen klaren Anfangspunkt gibt, handelt es sich in der Regel um Randbedingungen. Bei Gleichungen, die eine zeitliche Evolution beschreiben, ist es aber trotzdem oft der Fall, dass man zum Zeitpunkt \(0\) eine Startkonfiguration vorgibt und die Zeit vorwärts entwickelt. Dabei muss auf geeignete Weise definiert sein, was an den Rändern des Definitionsgebietes passieren soll. Formal kann man das Schreiben als:
\[D_r \mathbf{y} (\mathbf{x}, t) = \mathbf{r}(\mathbf{x}, t) \text{ für alle } (\mathbf{x}, t) \in R\] wobei \(R\) die Menge der Anfangs- oder Randpunkte ist, und \(D_r\) der lienare Operator, der ggf. Ableitungen oder schlichte Auswertungen (Identität) am Rand vorsieht.
Für die Lösung von Gleichungen mit allgemeinen Randbedingungen (egal ob DGL oder PDGL) reicht eine einfache Vorwärtsintegration, wie mit dem Eulerverfahren, nicht aus. Hier würde man statt dessen die gesamte Funktion \(\mathbf{y} (\mathbf{x}, t)\) diskretisieren (also in Abtastpunkte einteilen, und jeden dieser Werte als eine Unbekannte betrachten), und dann das Gleichungssytem lösen.
Finite Differenzen: Wenn man auf einem regelmäßgigen Gitter (“Array”) diskretisiert, spricht man von einem finite-Differenzen (FD) Ansatz. Wenn die Gleichung linear ist (also sowohl \(D\) wie auch \(F\) lineare Abbildungen im Parameter \(\mathbf{y}\) sind), dann erhält man nach der Diskretisierung einfache lineare Gleichungssysteme.
Finite Elemente: Schicker ist es, den Funktionenraum als Linearkombination von Basisfunktionen darzustellen: \[ \mathbf{y} (\mathbf{x}, t) = \sum_{i=1}^k \lambda_i \mathbf{b}_i(\mathbf{x}, t) \] Auch hier erhält man eine lineare Gleichung, wenn man diesen linearen Ansatz in die PDGL (oder, als Spezialfall, auch eine DGL) einsetzt: \[ D \mathbf{y} (\mathbf{x}, t) = F(\mathbf{y} (\mathbf{x}, t), \mathbf{x}, t) \text { wird zu} \] \[ \rightarrow D \left[ \sum_{i=1}^k \lambda_i \mathbf{b}_i(\mathbf{x}, t) \right] = F\left(\left[ \sum_{i=1}^k \lambda_i \mathbf{b}_i(\mathbf{x}, t) \right], \mathbf{x}, t\right) \] und wegen der linearität können wir das \(D\) und das \(F\) “ausklammern”: \[ \sum_{i=1}^k \lambda_i D \mathbf{b}_i(\mathbf{x}, t) = \sum_{i=1}^k \lambda_i F\left(\mathbf{b}_i(\mathbf{x}, t), \mathbf{x}, t\right). \] Und was wir erhalten, ist eine lineare Gleichung in den Unbekannten \(\lambda_i\). Mit Randbedingungen geht man ähnlich vor. Auch hier erhält man lineare Bedingungen:
\[D_r \mathbf{y} (\mathbf{x}, t) = \mathbf{r}(\mathbf{x}, t) \text{ für alle } (\mathbf{x}, t) \in R\] \[ \rightarrow \left[ \sum_{i=1}^k \lambda_i D_r\mathbf{b}_i(\mathbf{x}, t) \right] = \mathbf{r}(\mathbf{x}, t) \text{ für alle } (\mathbf{x}, t) \in R \]
Auch hier kann man lineare differentielle Bedingungen soweit in die Gleichung hereinziehen, dass man diese direkt auf die Basisfunktionen \(b_i\) anwenden kann. Oft kann man dies auch a priori berechnen, wenn man einen geeigneten analytischen Ausdruck für die Basisfunktionen hat.
Eigentlich ist das ganz einfach, aber es gibt noch 1-2 Haken an der Sache: - diskr - eins
Integration von Funktionen ist ebenfalls linear - daher kann man damit auch funktionale Gleichungen aufstellen, die (wegen der Linearität) relativ leicht zu lösen sind. In den Vorlesungsfolien wird dies etwas tiefer beleuchtet, mit dem Beispiel (pun intended) der Rendering-Equation, der zentralen Lichtausbreitungsgleichung aus der Computergraphik.
Wir schauen uns nun noch ein paar klassische Beispiele für DGLs und PDGLs an.
Ein klassisches Beispiel für (Systeme) von gewöhnlichen Differentialgleichungen sind die Newton’schen Bewegungsgleichungen.
Repräsentation: Wir modellieren hier \(n\) Partikel; dies sind bewegte Massenpunkte im Raum. Jedes Partikel hat \(3\) räumliche Koordinaten \(\mathbf{s}_i(t)\) und einen Geschwindigkeitsvektor \(\mathbf{v}_i(t) = \frac{d}{dt}\mathbf{s}_i(t)\). Die Zeit ist die unabhängige Variable, nach der wir Ableiten (wir betrachten also immer Änderungen über die Zeit). Die Objekte, die unsere Lösungen kennzeichnen, sind also Funktionen \(\mathbf{s}_1(t),...,\mathbf{s}_n(t),\mathbf{v}_1(t),...,\mathbf{v}_n(t)\), die wir über ein bestimmtes Zeitintervall \(t \in [a,b]\) verfolgen. Wir stecken alle die Positionen \(\mathbf{s}_i\) und Geschwindigkeiten \(\mathbf{v}_i\) in einen großen Zustandsvektor \(\mathbf{x}(t)\) mit der Dimension \(6n\).
Differentialgleichung: Für die Bewegungen gilt der bekannte Satz von Newton: \(\mathbf{F}=\mathbf{ma}\), also Kraft gleich Masse mal Beschleunigung. Die Beschleunigung \(\mathbf{a}\) ist die Zweite Ableitung des Ortes und die erste der Geschwindigkeit, \(\mathbf{a}=\dot{\mathbf{v}}=\ddot{\mathbf{s}}\). Für jedes einzelne Teilchen bekommen wir die Bewegungsgleichung: \[ \frac{d}{dt}\mathbf{s}_i(t) = \mathbf{v}_i(t)\\ \frac{d}{dt}\mathbf{v}_i(t) = \frac{1}{m_i}\mathbf{F}_i(t,\mathbf{x}(t))\\ \] Die Kräfte können dabei von allen anderen Partikeln abhängen, sowie von der Zeit (was eher selten benutzt wird). Stapelt man diese 6 Gleichungen pro Teilchen für alle \(n\) Teilchen übereinander, so hat man das System gewöhnlicher Differentialgleichungen, um die Bewegungen zu beschreiben.
Um ein konrektes Modell zu spezifizieren, muss man die Kräfte angeben. Hier gibt es eine Reihe von Standardkräften, die entweder einzeln auf ein Teilchen oder paarweise zwischen allen Paaren von Teilchen, die die entsprechende Eigenschaft haben, wirken: - Gravitation (paarweise): \(F_{ij} = \gamma \frac{m_im_j}{||\mathbf{s}_i-\mathbf{s}_j||^2}\). \(\gamma\) ist hierbei die Gravitationskonstante (die sehr klein ist; sowas wirkt nur richtig stark wenn mindestens eines der beiden Partikel die Masse eines Planeten o.ä. hat). - Elektrostatische Anziehung/Abstoßung (paarweise): \(F_{ij} = k_e \frac{q_i q_j}{||\mathbf{s}_i-\mathbf{s}_j||^2}\). \(k_e\) ist hierbei die Coulombkonstante (die deutlich größer ist als \(\gamma\)), und \(q_i,q_j\) sind die (vorzeichenbehafteten) elektrischen Ladungen der Teilchen. - Hooksche Federn (paarweise): \(F_{ij} = l (d_{ij}^{(0)}-||\mathbf{s}_i-\mathbf{s}_j||)\frac{\mathbf{s}_i-\mathbf{s}_j}{||\mathbf{s}_i-\mathbf{s}_j||}\). Die Kraft steigt linear mit der Auslenkung, und wirkt dieser entgegen. \(d_{ij}^{(0)}\) ist dabei die Ruhelänge der Feder zwischen Partikel \(i\) und \(j\), und \(l\) ist die Federkonstante (wie stark die Rückstellkraft ist). Die Formel gilt für lineare Federn. Bei nicht allzustarken Auslenkungen sind die meisten mechanischen Federn linear. - Gleit- / Haftreibung (einzeln): \(F_i = -\mu \frac{\mathbf{v}_i}{||\mathbf{v}_i||}\) - die Kraft ist konstant (\(\mu\) gibt an, wie stark gebremst wird). Für Geschwindigkeit \(\mathbf{v}_i=\mathbf{0}\) gibt es keine Kraft, die wirkt. - Strömungsreibung in Fluiden, z.B. Luft (einzeln): \(F_i = -\mu \mathbf{v}_i \cdot ||\mathbf{v}_i||\). Die Kraft ist steigt quadratisch mit der Geschwindigkeit (\(\mu\) gibt an, wie stark gebremst wird; das hängt von der Form des Objektes und des Mediums (z.B. Luft, Wasser) ab).
Man kann sich auch noch eine ganze Reihe anderer Kräfte ausdenken, um damit einen Simulator für Ensembles von bewegten Massenpunkten zu bauen.
Video: Beispiel für eine ODE - eine Simulation des Sonnensystems (mit einigen Asteroiden in grün, die an einer Stelle eingefügt werden), basierend auf den Newtonschen Gravitationsgleichungen und mit einem expliziten Euler-Verfahren (mit Laufenden Updates, für Energieerhaltung) als Integrator. Nach 5 Sekunden wird die Simulation stark beschleunigt (mehrere Zeitschritte pro Frame).
Siehe Vorlesungsfolien.
Siehe Vorlesungsfolien.
Aufgabe 3.1: Warum ist die Ableitung eine lineare Operation? Erinnern sie sich an die Rechenregeln aus der Schule/Grundvorlesung. Was ist der Kern dieser Operation?
Aufgabe 3.2: Welche Arten von Integration über Funktionen können als lineare Operationen aufgefasst werden, und welche nicht?
Aufgabe 3.3: Wenn man eine Funktion durch eine regelmäßig abgetastete, diskrete Repräsentation (Array) ersetzt, dann sind Ableiten, Integrieren und andere lineare Abbildungen alle gleichermaßen durch Matrizen darstellbar. Wie sieht die Matrix für eine (approximative) Ableitung bzw. Integration aus?
Aufgabe 3.4: Bestimmen Sie analytisch die Menge aller Lösungen (welche ein linearer Raum ist) der Differentialgleichung \(\frac{d}{dt} f(t) = \lambda f(t)\). \(f\) bildet dabei von \(\mathbb{R}\) nach \(\mathbb{R}\) ab. Bestimmen Sie danach die Lösung für \(f(0)=a\).
Aufgabe 3.4: Bestimmen Sie analytisch die Menge aller Lösungen (auch ein Unterraum) der Differentialgleichung \(\frac{d}{dt} \mathbf{f}(t) = \mathbf{M} \mathbf{f}(t)\). \(\mathbf{f}\) bildet dabei von \(\mathbb{R}\) nach \(\mathbb{R}^d\) ab, und \(\mathbf{M}\) ist eine symmetrische Matrix. Bestimmen Sie danach die Lösung für \(\mathbf{f}(0)=\mathbf{a}\).
Aufgabe 3.5: Bestimmen Sie analytisch die Menge aller Lösungen der Differentialgleichung \(\frac{d}{dt} \mathbf{f}(t) = \mathbf{M}(t) \mathbf{f}(t)\). \(\mathbf{f}\) bildet dabei von \(\mathbb{R}\) nach \(\mathbb{R}^d\) ab, und \(\mathbf{M}(t)\) ist eine matrixwertige Funktion, die von von \(\mathbb{R}\) nach \(\mathbb{R}^{d \times d}\) abbildet. Die Matrix \(\mathbf{M}(t)\) ist zu jedem Zeitpunkt symmetrisch. Bestimmen Sie danach die Lösung für \(\mathbf{f}(0)=\mathbf{a}\).
In diesem Kapitel schauen wir uns an, wie man Funktionen approximativ durch vorgegebene Punkte legen kann, auch bekannt als “Regressionsproblem”. Als Technik benutzen wir die Methode der kleinsten (Fehler-) Quadrate, auf Englisch als “least-squares”-Methode bekannt. Wie üblich beschränken wir uns auf lineare Ansätze.
Viele Phänomene in der Natur sind normalverteilt: Nehmen wir an, dass wir eine reele Zufallsvariable \(X\) beobachten, die im Mittel den Wert \(\mu \in \mathbb{R}\) annimmt und im Mittel mit Standardabweichung \(\sigma > 0\) schwankt. Die Gaußsche Normalverteilung ist diejenige Wahrscheinlichkeitsverteilung \(p:\mathbb{R} \rightarrow \mathbb{R}\), die 1. Dies beiden Eigenschaften hat (\(\mu,\sigma\)). 2. Ansonsten “so zufällig wie möglich” ist (formal: die Entropy \(H(p)\) ist maximal)
Ein anderer Grund, warum die Normalverteilung so Häufig auftritt, ist, dass die Summe von unabhängigen reellen Zufallsvariablen dazu tendiert, eine Normalverteilung zu bilden: Je mehr Summanden addiert werden, umso stärker sieht die Verteilung der Summe wie eine Normalverteilung aus. Damit dies funktioniert, müssen nur relativ schwache “technische” Bedinungen erfüllt sein (neben Unabhängigkeit vor allem die Existenz von Erwartungswert und Varianz bei allen Summanden). Das ganze ist als zentraler Grenzwertsatz bekannt.
tl;dr – Zufällige Phenomäne, bei denen viele verschiedene unabhängige, zufällige Aspekte (additiv) zusammenkommen sind meistens normalverteilt.
Wahrscheinlichkeitsdichte
Die Gaußsche Normalverteilung (in 1D) hat die Dichte:
\[ p(x) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]
Der Faktor vor dem e-hoch-Term dient zur Normalisierung (\(\int_\mathbb{R} p = 1\)). Was bleibt ist ein quadratisches Polynom \[ E(x)=\frac{1}{2\sigma ^2}\left(x^2 -2x\mu +\mu^2\right) \] in \(x\), welches in das e-hoch-minus (\(x\mapsto \exp (- x )\)) eingesetzt wird. Die Funktion \(E(x)\) is auch als neg-log-Wahrscheinlichkeitsdichte bekannt.
Will man also Normalverteilungen besser verstehen, dann muss man mit quadratischen Polynomen umgehen können.
Witzig ist, dass Produkte von Normalverteilungen (wenn man also unabhängige Zufallsexperimente hintereinanderausführt, und entsprechend die Dichten multipliziert), wieder Normalverteilungen ergeben. Dabei addieren sich die neg-log-Dichten einfach (Grund: \(e^{-x} \cdot e^{-y} = e^{-(x+y)}\)), und dass bedeutet, dass sich die Koeffizienten der quadratischen Polynome addieren.
Mehrdimensionale Verteilungen
Man kann die Sache mit der Multiplikation auch machen, wenn es mehr als eine Größe \(x \in \mathbb{R}\) gibt, die man beobachten kann. Nehmen wir also an, dass wir \(n\) Zufallsvariablen \(X_1,...,X_d\) haben, die unabhängig voneinander sind, und Normalverteilt mit dem gleichen Erwartungswert \(\mu\) und Standardabweichung \(\sigma\). Die gemeinsame Verteilung (mehrdimensionale Dichtefunktion) dieser Variablen ist dann:
\[ p(x_1,...,x_d) = \left(\frac{1}{\sigma\sqrt{2\pi}}\right)^d \exp\left(-\frac{(x_1-\mu)^2+\cdots+(x_d-\mu)^2}{2\sigma^2}\right) \]
oder in Vektorschreibweise mit \(\mathbf{x}=[x_1,...,x_d]^T\) und \(\boldsymbol{\mu}=[\mu,...,\mu]^T\):
\[\begin{eqnarray} p(\mathbf{x}) &=& \frac{1}{(2\pi)^{n/2}\sigma^d} \exp\left(-\frac{\left(\mathbf{x}-\boldsymbol{\mu}\right)^2}{2\sigma^2}\right) \\ &=& \frac{1}{(2\pi)^{n/2}(\det{\Sigma})^{-1/2}} \exp\left(-\frac{1}{2}\left(\mathbf{x}-\boldsymbol{\mu}\right)^T\boldsymbol{\Sigma}\left(\mathbf{x}-\boldsymbol{\mu}\right)\right) \text{ mit } \boldsymbol{\Sigma} = \sigma^2 \mathbf{I} \end{eqnarray}\]
Die Form der letzten Formel fällt hier “vom Himmel”. Dies ist die (allgemeine) Schreibweise für eine Multivariate (mehrdimensionale) Normalverteilung – wir sehen etwas später, warum das Sinn macht.
Der Witz ist auch hier wieder, dass wir im Exponenten nichts anderes als ein (multivariates) quadratisches Polynom haben.
Schauen wir uns also quadratische Polynome in mehrere Variablen genauer an. Wir sind an Polynomen mit maximalem “totalem Grad” zwei interessiert, d.h., dass sich in jedem Koordinatensystem (für die Eingabevariablen) maximal ein quadratisches Polynom ergibt. Beispielsweise ist \((x,y) \mapsto x^2 \cdot y\) eine kubische Funktion, wenn man im \(x,y\)-Raum diagonal läuft. Damit wir quadratisch bleiben, muss der gemischte Grad (über alle Variablen) höchstens zwei sein. Dies ergibt die folgende allgemeine Form:
\[ f(x_1,..,x_d) = \sum_{i=1}^d \sum_{j=1}^d a_{i,j} x_i x_j + \sum_{i=1}^d b_i x_i + c \] mit Koeffizienten \[ a_{i,j}, b_i, c \in \mathbb{R},\ \ \ i,j \in \{1,...,d\} \]
Dies kann man in Matrixform schreiben als:
\[ f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b} \mathbf{x} + c \] mit \[ \mathbf{A} = \left(\begin{array}{ccc} a_{1,1} & \cdots & a_{d_1} \\ \vdots & \ddots & \vdots \\ a_{d,1} & \cdots & a_{d_d} \end{array}\right), \mathbf{b} = \left(\begin{array}{c} b_1 \\ \vdots \\ b_d \end{array}\right), \mathbf{x} = \left(\begin{array}{c} x_1 \\ \vdots \\ x_d \end{array}\right) \]
Die Matrix \(\mathbf{A}\) kann man dabei immer symmetrisch wählen, also mit \(a_{i,j} = a_{j,i}\) bzw., equivalent, mit \(\mathbf{A}^T =\mathbf{A}\), da die Multiplikation von \(x_i \cdot x_j\) kommutativ ist.
Machen wir das ab jetzt immer. Wenn \(\mathbf{A}\) symmetrisch ist, dann ist sie immer diagonalisierbar \(\mathbf{A} = \mathbf{U} \boldsymbol{\Lambda} \mathbf{U}^T\) mit einer orthogonalen Eigenbasis \(\mathbf{u}_1, ..., \mathbf{u}_d\) und Eigenwerten \(\lambda_1,...,\lambda_d\).
Quadratische Formen
Um zu verstehen, wofür das gut ist, müssen wir verstehen, was der quadratische Teile \(\mathbf{x}^T \mathbf{A} \mathbf{x}\) eigentlich macht, und was der Rest macht. Schauen wir uns dazu erstmal ein rein Quadratisches Polynom an:
\[ f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x} \]
Der Schnitt in verschiedene Richtungen sind offensichtlich einfach nur Parabeln. Wenn man in die Eigenrichtungen geht, kennen wir auch die Koeffizienten: \[ f(u_1,...,u_d) = \sum_{i=1}^d \lambda_i u_i^2 \] Dabei sind \(u_i\) die Koordinaten in den Achsen \(\mathbf{u}_i\). Qualitativ können drei Dinge passieren: Die Eigenwerte können positiv, negativ oder null sein. Und das ganze kann man, für \(d \ge 2\), auch mischen. Man erhält damit folgende Grundformen:
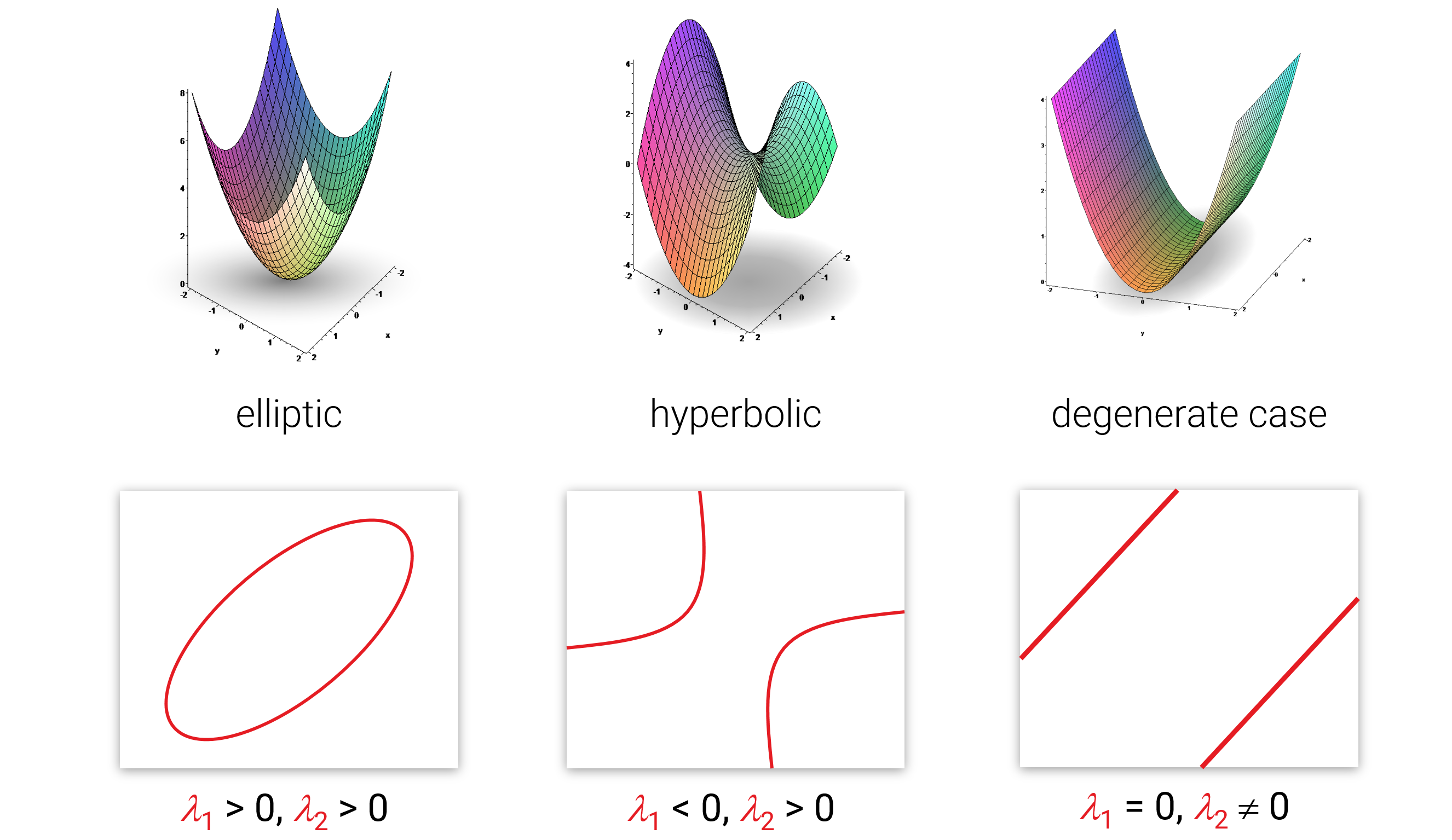
Um den allgemeinen Fall eines quadratischen Polynoms zu verstehen, können wir uns die “Scheitelpunktsform” anschauen, in der wir die “Spitze” bzw. den Scheitelpunkt des Gebildes vom Ursprung in den Punkt \(\boldsymbol{\mu}\) verschieben:
\[\begin{eqnarray} & & (\mathbf{x} - \boldsymbol{\mu})^T \mathbf{A} (\mathbf{x} - \boldsymbol{\mu}) \\ &=& \mathbf{x}^T \mathbf{A} \mathbf{x} + 2 \boldsymbol{\mu}^T \mathbf{A} \mathbf{x} +\boldsymbol{\mu}^2 \end{eqnarray}\]
Was man hier sieht, ist dass die Form des Funktionsgraphen nur von den rein quadratischen Koeffizienten \(\mathbf{A}\) abhängt, dass der lineare Anteil \(\mathbf{b}\) den Graphen in der Ebene verschiebt, und dass \(c\) (offensichtlich) den Graphen in Ausgaberichtung nach oben und unten verschiebt.
Die allgemeine multi-variate Normalverteilung
Nachdem wir das genauer verstanden haben, können wir uns nochmal die multi-variate Normalverteilung anschauen. Die Form mit unabhängigen Variablen mit gleichem Mittelwert und Standardabweichung war lediglich das Produkt von 1D Verteilungen. Allgemein können wir uns eine Form
\[ p(\mathbf{x}) = \frac{1}{\int_{\mathbb{R}^d} p} \exp\left( - \mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b} \mathbf{x} + c \right) \]
vorstellen. Zwingend ist dabei, dass die Eigenwerte von \(\mathbf{A}\) alle echt größer als \(0\) sind, \(\lambda_i>0\), da man sonst, offensichtlich, die Normalisierung (Integral im Nenner) nicht berechnen kann. Ansonsten ist allerdings tatsächlich alles möglich, wie die folgende Rechnung zeigt:
Starten wir mit einer Einheits-Gaussverteilung, d.h., wir haben \(d\) unabhängige Zufallsvariablen \(x_1,...,x_d \in \mathbb{R}\), zusammengefasst in \(\mathbf{x} \in \mathbb{R}^d\), mit Erwartungswerten \(\mu_1,...,\mu_d = 0\), zusammengefasst in \(\boldsymbol{\mu} \in \mathbb{R}^d\) und Standardabweichungen \(\sigma_1,...,\sigma_d = 1\). Die Dichtefunktion ist dann gegeben durch
\[ p(\mathbf{x}) = \frac{1}{\int_{\mathbb{R}^d} p} \exp\left( - \frac{1}{2} (\mathbf{x}^T \mathbf{I} \mathbf{x}) \right) \]
Wir können nun das Koordinatensystem von \(\mathbf{x}\) beliebig ändern. Sei also \(\mathbf{T}\in GL(d)\) eine beliebige invertierbare Matrix (\(GL(d)\) ist die Menge von invertierbaren \(d \times d\)-Matrizen), dann können wir entsprechend \(\mathbf{x} = \mathbf{T}\mathbf{x}\) ersetzen, um mit neuen, transformierten \(\mathbf{x}\) zu rechnen. Eingesetzt ergibt das: \[ p(\mathbf{x}) = \frac{1}{\int_{\mathbb{R}^d} p} \exp\left( - \frac{1}{2} (\mathbf{x}^T \mathbf{T}^T \mathbf{T} \mathbf{x}) \right) \] (Bemerkung: die Normalisierungskonstante \(\int_{\mathbb{R}^d} p\) ändert sich auch, da das Integrationsgebiet nun anders parametrisiert ist; der Korrekturfaktor ist \((\det{T})^{-1}\), wie bereits in der zuvor weiter oben angegebenen Gleichung eingeplant).
Wenn man zusätzlich noch den Erwartungswert ändern will, muss man die ganze Funktion im \(\mathbf{x}\)-Raum verschieben: \[ p(\mathbf{x}) = \frac{1}{\int_{\mathbb{R}^d} p} \exp\left( - \frac{1}{2} ((\mathbf{x}^T -\boldsymbol{\mu})\mathbf{T}^T \mathbf{T} (\mathbf{x}^T -\boldsymbol{\mu})) \right) \] Insgesamt ergibt sich ein neues quadratisches Polynom, bei dem die Quadratischen Koeffizienten durch die Matrix \(\Sigma^{-1} := \mathbf{T}^T \mathbf{T}\) gegeben sind. Man nennt diese Matrix die inverse Kovarianzmatrix. Anschaulich bewirkt eine Verzerrung des Koordinatensystems, dass die Gausverteilung vergrößert oder verkleinert und eventuell elliptisch verzerrt wird. Dadurch sind die Variablen nicht mehr unabhängig voneinander – daher der Name.

Das ist alles!
In der Statistik ist die Multivariate Normalverteilung für eine \(d\)-dimensionale Zufallsvariable \(\mathbf{x} \in \mathbb{R}^d\) definiert als: \[ p(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^d \det{\Sigma}}} \exp\left(-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}-\boldsymbol{\mu})\right) \]
mit Parametern \(\boldsymbol{\mu} \in \mathbb{R}^d\) und \(\boldsymbol{\Sigma} \in \mathbb{R}^{d \times d}\). Dabei muss \(\boldsymbol{\Sigma}\) eine symmetrisch-positiv-definite Matrix (“SPD-Matrix”) sein, also \(\boldsymbol{\Sigma} = \boldsymbol{\Sigma}^T\) und \(\boldsymbol{\Sigma} > 0\) (wobei letzteres bedeutet, dass die Eigenwerte alle größer als Null sein müssen. Man beachte: die Eigenwerte existieren immer wegen der Symmetrie).
Wir beweisen nun, dass dies alles equivalent zur Änderung des Koordinatensystem mit einer invertierbaren Matrix \(\mathbf{T}\) ist (das man \(\boldsymbol{\mu}\) frei wählen kann, ist klar). Wir haben schon gesehen, dass eine Änderung des Koordinatensystems eine andere Kovarianzmatrix (bzw. deren Inverses) produziert. Dies Matrix ist immer symmetrisch und positiv definit. - Sie ist symmetrisch, da Produkte \(\mathbf{T}^T \mathbf{T}\) immer symmetrisch sein müssen. Beweis mit den Rechenregeln der Matrixalgebra: \([ \mathbf{T}^T \mathbf{T} ]^T = \mathbf{T}^T [\mathbf{T}^T ] ^T = \mathbf{T}^T \mathbf{T}\). - Außerdem ist sie positiv definit, also alle Eigenwerte sind positiv. Beweis dazu: Wir können nach der Singulärwertzerlegung (die wir hier voraussetzen) immer \(\mathbf{T} = \mathbf{U}\mathbf{D}\mathbf{V}^T\) schreiben, mit orthogonalen \(\mathbf{U},\mathbf{V}\) und diagonalen \(\mathbf{D}\). Die Diagonalmatrix \(\mathbf{D}\) kann keine Nullen enthalten, sonst wäre sie nicht invertierbar. Entsprechend ist \[\mathbf{T}^T \mathbf{T} = [\mathbf{V}\mathbf{D}\mathbf{U}^T] \mathbf{U}\mathbf{D}\mathbf{V}^T =\mathbf{V}\mathbf{D}^2\mathbf{V}^T\] Und das ist offensichtliche eine positiv-definite Matrix (sie sieht übrigens auch ziemlich symmetrisch aus).
Witzig ist, dass das umgekehrte auch stimmt: Nehmen wir eine SPD-Matrix \(\mathbf{A}\) und schreiben Sie via Diagonalisierung als \(\mathbf{A} = \mathbf{U} \mathbf{D} \mathbf{U}^T\) (das geht immer wegen der Symmetrie). Dann können wir mit \(\mathbf{T} := \mathbf{U} \sqrt{\mathbf{D}}\) eine “Wurzel” angeben, für die offensichtlich gilt \(\mathbf{T}^2 = \mathbf{A}\). Mit \(\sqrt{\mathbf{D}}\) ist dabei gemeint, bei der Diagonalmatrix bei allen Eigenwerten die Wurzel zu ziehen. Das geht auf jeden Fall, da alle \(\lambda_i>0\) nach Voraussetzung (das PD in SPD).
Angewandt auf die Kovarianzmatrix erhält man die Aussage (dabei muss man sich noch klarmachen, dass \(\boldsymbol{\Sigma}\) genau dann SPD ist, wenn \(\boldsymbol{\Sigma}^{-1}\) SPD ist; das sieht man aber sofort in der Diagonalisierung).
Bemerkung: Wir haben hier noch ein paar andere, interessante Dinge gesehen:
Die allgemeine Idee von least-squares Verfahren ist es, den Wunsch ein bestimmtes Ziel zu erreichen als quadratische Fehlerfunktion oder Zielfunktion (english “loss-function”, “objective function”) auszudrücken. Mehrere solche Ziele können dann zu einer gesamtfunktion (durch Addition der Einzelfunktionen) kombiniert werden. Danach kann man das Optimum bestimmen, indem man den Wert der Fehlerfunktion minimiert. Für rein quadratische Funktionen ist dies immer direkt durch das Lösen eines lineare Gleichungssystems möglich.
Im Detail: Sei im folgenden \(\mathbf{x}\) ein unbekannter Vektor. Dann drücken wir das erste Ziel aus, indem wir eine qudratische Zielfunktion \[ E_1(\mathbf{x}) = \mathbf{x}^T \mathbf{A}_1 \mathbf{x} + \mathbf{b}_1 \mathbf{x} + c_1 \] Dabei müssen die Matrix \(\mathbf{A}_1 \ge 0\) sein, also semi-positiv-definit (bei negativen Eigenwerten gibt es beliebig kleine Fehlerwerte; die Minimierung macht dann keinen Sinn mehr).
Wahrscheinlich haben wir nicht nur einen Wunsch, sondern viele, sagen wir mal \(n\) Stück. Dann erhält man:
\[\begin{eqnarray} E(\mathbf{x}) &=& \sum_{i=1}^n E_1(\mathbf{x}) \\ &=& \sum_{i=1}^n \mathbf{x}^T \mathbf{A}_i \mathbf{x} + \mathbf{b}_i \mathbf{x} + c_i \\ &=& \mathbf{x}^T \left[ \sum_{i=1}^n \mathbf{A}_i \right] \mathbf{x} + \left[ \sum_{i=1}^n \mathbf{b}_i \right] \mathbf{x} + \left[ \sum_{i=1}^n c_i \right] \\ &=:& \mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b} \mathbf{x} + c \\ \end{eqnarray}\]
Sobald wir diese finale Zielfunktion (wir lassen hier als Notation einfach die Indices \(i\) weg) berechnet haben, können wir, wie wir oben gesehen haben, den “Scheitelpunkt” der quadratischen Funktion berechnen:
\[\begin{eqnarray} & &\mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b} \mathbf{x} + c \rightarrow min.\\ &\Leftrightarrow& 2 \mathbf{A} \mathbf{x} = - \mathbf{b} \end{eqnarray}\]
Diese Bedingung kann man bekommen, indem man den Gradienten \(\nabla_\mathbf{x} E(\mathbf{x}) = 0\) setzt: Dies ist eine notwendige Bedingung für Optimalität einer jeden glatten Zielfunktion und hinreichend, da die Funktion quadratisch ist.
Alternativ kann man die Punkt-Scheitelpunktform, wie weiter oben hergeleitet, ansehen, und die Koeffizienten vergleichen:
\[\begin{eqnarray}(\mathbf{x} - \boldsymbol{\mu})^T \mathbf{A} (\mathbf{x} - \boldsymbol{\mu}) &=& \mathbf{x}^T \mathbf{A} \mathbf{x} - 2 \boldsymbol{\mu}^T \mathbf{A} \mathbf{x} +\boldsymbol{\mu}^2 \\ &=& \mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b} \mathbf{x} + c \\ \rightarrow 2\mathbf{A} \boldsymbol{\mu} &=& - \mathbf{b} \\ \rightarrow \boldsymbol{\mu} &=& -\frac{1}{2} \mathbf{A}^{-1} b \ \ \ \ \ \text{ falls $\mathbf{A}$ invertierbar } \end{eqnarray}\]
Ein wichtiges Beispiel ist das “Fitten” (auf Deutsch vielleicht “Anpassen”, “Annähern”, aber irgendwie sagen alle immer “fitten”) von Funktionen an Datenpunkte (typischerweise aus einer Messung oder Erhebung, die mit erheblichem Rauschen belegt ist). Das Problem ist besonders einfach zu lösen, falls wir Funktionen aus einem (endlich-dimensionalen) linearen Unterraum betrachten. Anders gesagt, wir suchen eine Funktion \[ f: \mathbb{R}^{d_1} \supseteq \Omega \rightarrow \mathbb{R}^{d_2} \] die als Linearkombination von Basisfunktionen gegeben ist: \[ f(\mathbf{x}) = \sum_{i=1}^k \lambda_i b_i(\mathbf{x}). \] Dabei sind \[ b_i: \mathbb{R}^{d_1} \supseteq \Omega \rightarrow \mathbb{R}^{d_2} \] Fix gewählte Basisfunktionen (die werden nicht mitoptimiert), und \[ \lambda_1,...,\lambda_k \in \mathbb{R} \] sind die Koordinaten der gesuchten Funktion \(f\) im Unterraum \(\operatorname{span}\{b_1,..,b_k\}\). Wir haben nun Datenpunkte \[ (\mathbf{x}_j, \mathbf{y}_j) \in \mathbb{R}^n \times \mathbb{R}^m, \text{ für } j=1..n \] gegeben, die in \(y\)-Richtung normalverteilt durch Rauschen gestört sind (mit konstanter Kovarianzmatrix \(\sigma \mathbf{I}\) für alle Punkte) und möchten, dass \[ \sum_{j=1}^n ||f(\mathbf{x}_j) - \mathbf{y}_j||^2 \rightarrow min. \] so klein wie möglich wird. Setzt man in diesen Ausdruck den linearen Ansatz mit Basisfunktionen ein, so erhält man (offensichtlich) ein multi-variates quadratisches Polynom in \(\lambda_1,...,\lambda_k\), welches man wie oben erläutert optimieren kann (die Vorlesungsfolien gehen hier noch etwas mehr ins Detail). Man sieht auch relativ leicht (die Vorlesungsfolien zeigen eine formale Herleitung), dass dies genau eine Normalverteilung der Fehler in den \(\mathbf{y}_j\) unter der Annahme ungestörter \(\mathbf{x}_j\) modelliert, wobei der Fehler Mittelwert \(\mu=0\) und konstante Standardabweichung \(\sigma\) hat. Für andere Fälle muss man systematische Fehler \(\mu\neq 0\) vorher abziehen, bzw. die quadratischen Fehler mit \(1/\sigma^2\) gewichten (letzteres ist auch in den Vorlesungsfolien genau hergeleitet).
Wie in den Vorlesungsfolien hergeleitet, erhält man das folgende lineare Gleichungssystem, dass die Lösung beschreibt:
\[ \left(\begin{array}{ccc} \langle b_1, b_1 \rangle & \cdots & \langle b_k, b_1 \rangle \\ \vdots & \ddots & \vdots \\ \langle b_1, b_k \rangle & \cdots & \langle b_k, b_k \rangle \end{array}\right) \cdot \left(\begin{array}{c} \lambda_1 \\ \vdots \\ \lambda_k \end{array}\right) = \left(\begin{array}{c} \langle b_1, y \rangle \\ \vdots \\ \langle b_1, y \rangle \end{array}\right) \] Hierbei steht das “Skalarprodukt” \(\langle\cdot,\cdot\rangle\) für das folgende “datenabhängige Skalarprodukt” \[ \langle b_i, b_j \rangle := \sum_{l=1}^n b_i(x_l) \cdot b_j(x_l) \ \ \ \text{ und } \ \ \ \langle b_i, y \rangle := \sum_{l=1}^n b_i(x_l) \cdot y_l \] Anmerkung: Man kann hier auch die Standardskalarprodukte nutzen, um eine kontinuierliche Funktion \(y\) durch eine Summe von Basisfunktionen im least squares Sinne \[\left\lvert\left\lvert\sum_{i=1}^k \lambda_i b_i - y \right\rvert\right\rvert^2 = \left\lvert\left\lvert f - y \right\rvert\right\rvert^2 = \langle f-y,f-y\rangle \rightarrow min.\] zu approximieren.
Was macht man wenn die Verteilung keine Normalverteilung ist? Zunächst ist das tatsächlich ein praxisrelevantes Problem. Die Wahrscheinlichkeit, bei einer Normalverteilung mehrere Standardabweichungen vom Mittelwert abzuweichen ist klein - sie nimmt exponentiell mit einem Faktor \(\sigma \mapsto c\cdot \sigma\) ab, in der Form \(\mathcal{O}(\exp(-c^2))\). Sollten die Daten z.B. “Ausreisser” enthalten, die sehr weit abweichen, und nicht aus der Normalverteilung stammen, so dominieren diese leicht die Lösung.
Why care? Mein Lieblingsbeispiel hierfür (aus eigener praktischer Erfahrung) ist ein Messgerät (2D Laserscanner), dass aufgrund eines Fehlers in der seriellen Schnittstelle jeden 100sten Messwert durch eine völlig falsche Zahl ersetzt hatte. Im konkreten Fall hat das Gerät Abstände zu Objekten in Millimetern zurückgegeben, mit einem maximalen Abstand von einigen hundert Metern (einigen tausend mm). Bei Fehlern wurde jedoch eine Zufallszahl über den gesamten 16bit Zahlenraum (gleichverteilt über \(0....65535\)) statt Werte im Bereich von ca. 1000 mit \(\sigma=20-30~\text{mm}\)) - ein least-squares-Fit an die Daten lieferte völlig unbrauchbare Ergebnisse (Etwas vereinfacht: Die Daten sollten segmentweise aus einfachen Geraden bestehen, da der Scanner Gebäude gescannt hat; dies könnte man mit linearer Regression “fitten”; mit den Ausreißern würden solche Gerade aber nicht zuverlässsig erkannt; das wirkliche Problem war noch etwas komplizierter - siehe dieses Paper, dass Kollegen von zu diesem Thema geschrieben haben).
What can we do?
Die statistisch richtige Antwort ist, eine andere Verteilung als die Normalverteilung anzunehmen, bei der stark abweichende Ergebnisse nicht dermaßen unwahrscheinlich sind. Im Beispiel des kaputten Laserscanners könnte man dies wie folgt modellieren: Sei \(x\in \mathbb{R}\) die Entfernung in Millimetern (wir ignorieren die 16Bit Quantisierung; tatsächlich wurden die Messungen in Millimetern aufgelöst), dann ist die Wahrscheinlichkeit, einen Punkt in Abstand \(x\) zu beobachten, wenn der tatsächliche Abstand \(\mu\) betrug:
\[p(x) = \lambda \ \ \cdot \underbrace{\frac{1}{65535}}_{\begin{array}{c}\text{\scriptsize Gleichverteilung}\\ \text{\scriptsize auf 0..65535}\end{array}} + \ \ \ (1-\lambda)\ \ \ \cdot \underbrace{\mathcal{N}(\mu,\sigma)}_{\text{Normalverteilung}} \] wobei z.B. \[ \sigma = 30 \text{ [mm]} \] die Standardabweichung (Scannergenauigkeit) ist, und \[\lambda = \frac{1}{100}\] die Wahrscheinlichkeit für einen Ausreißer ist. Die Verteilung, die man erhält, entspricht einer Normalverteilung auf einem “Teppich” einer Gleichverteilung:
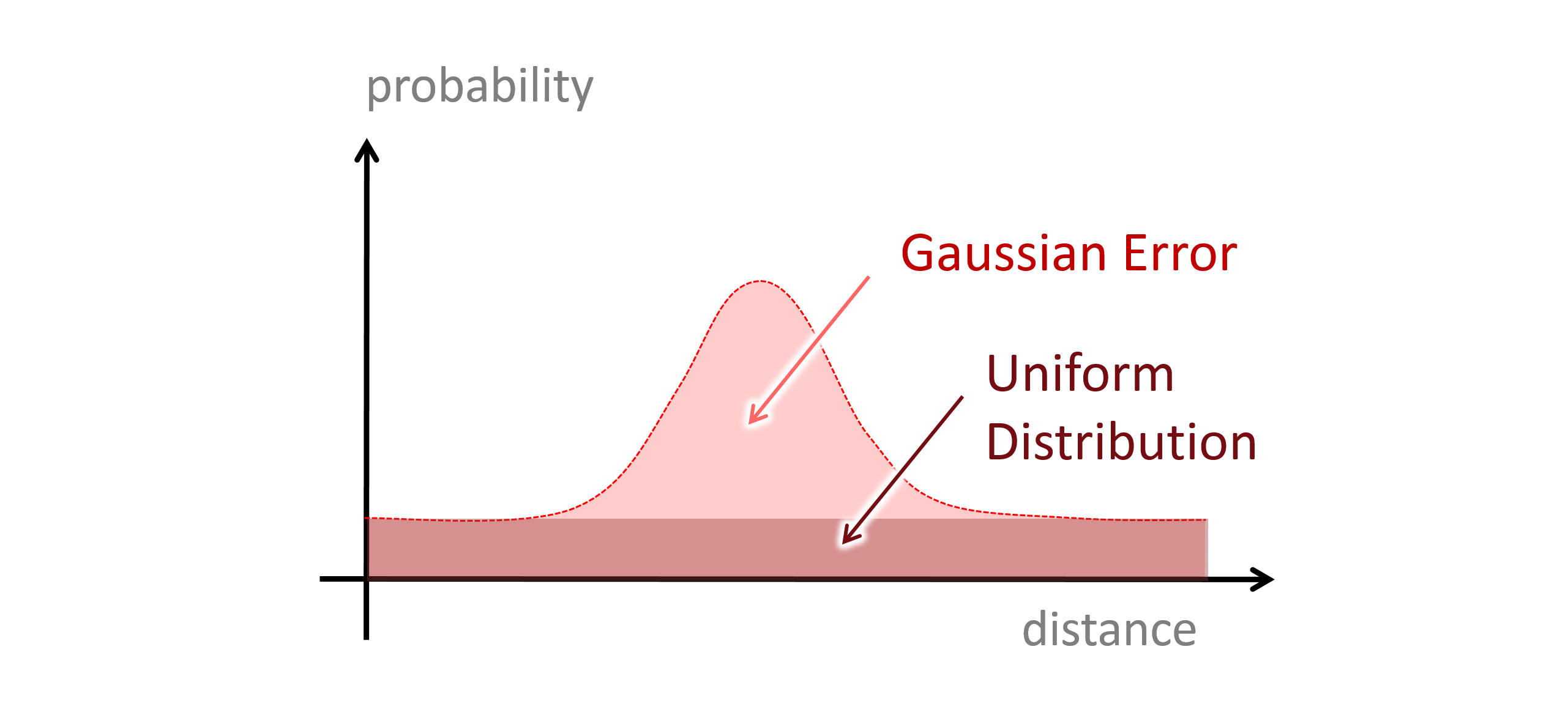
Wie rechnet man dass?
Wenn man eine solche Mixtur in die Herleitung des Least-Square-Fehlers einsetzt, dann stellt man leider fest, dass man kein “schönes” Gleichungssystem herleiten kann - es bleibt erstmal nur eine einfach numerische Optimierung, z.B. via Gradientenabstieg. Bei der Mixtur aus Gauss- und Gleichverteilung kommt erschwerent hinzu, dass man keine analytische Lösung für den Logarithmus der Verteilung finden kann. Man behilft sich daher oft mit Truncation - man schneidet die log-likelihood (also den quadratischen Fehler) einfach ab, sobald ein Schwellwert überschritten wurde. Dies entspricht qualitativ (auch wenn nicht genau) dem oben beschriebenen Mixturmodell und funktioniert in praktischen Anwendungen oft gut (Idee: Wenn der Fehler zu groß ist, war es wohl ein Ausreißer, und wir ignorieren ihn einfach, d.h., erhöhen die Strafe nicht weiter als den Schwellwert; es macht damit immer noch Sinn, die Anzahl der Ausreißer zu minimieren).
Die Sache hat noch ein zweites Problem: Die oben beschriebene “robuste” Verteilung (Normal+etwas Gleichverteilung, oder alternativ eine Normalverteilung mit Maximalwert für den quadratischen Fehler) ist keine konvexe Funktion. Konvexe Funktionen biegen sich immer nur in eine Richtung; addiert man diese, so erhält man immer nur ein globales Minimum. Die abgeschnittene quadratische Fehlerfunktion sieht aber eher aus wie ein “Schlagloch” - addiert man mehrere davon, so erhält man viele verschiedene Schlaglöcher in der Gesamtfunktion - es gibt also mehrere lokale Minima.
Das ist kein Problem, wenn man schon eine gute Schätzung für die Lösung hat, und nur ein wenig Nachoptimieren möchte. Hat man aber keine Idee, was die Lösung sein könnte, und sucht diese z.B. von einer zufälligen Initialisierung der \(\lambda_1,...,\lambda_k\) aus, dann besteht u.U. ein sehr hohes Risiko, in einem sub-optimalen lokalem Minimum zu landen (bei dem abgeschnittenen Modell heißt das in der Regel, dass wir nicht die Minimale Zahl von Ausreißern gefunden haben, sondern zu viele Daten als Ausreißer ansehen, da das rekonstruierte Modell schlicht ziemlich falsch ist).
Um das zu verhindern, benutzt man oft statt eines Mixturmodells, wie oben beschrieben, ein “zu strenges” Modell, welches Ausreißer doch noch gewichtet, dafür aber Konvex ist (also sich immer in die gleiche Richtung biegt). Populär ist die “Laplaceverteilung”, entsprechend eines \(\ell_1\)-Norm statt eines \(\ell_2\) (least-squares) Fehlermaß: \[ p(x) = \frac{1}{2\sigma} \exp \left(-\frac{1}{\sigma}|x-\mu|\right), \ \ \ \text{ d.h. } \ \ \ E(x) = \frac{|x-\mu|}{\sigma}. \] Diese Verteilung ist weniger “empfindlich” gegen Ausreißer (sie werden nur linear statt quadratisch bestraft, und das hat durchaus einen erheblichen Einfluß) und man kann, zumindest theoretisch, mit einem Gradientenabstieg immer eine global optimale Lösung finden.
Das Design eines Gradientenabstiegsverfahrens für solche Zielfunktionen (konvex oder nicht), ist konzeptionell simple (bergab = \(-\nabla E\) wird’s besser), in der Praxis führt das aber oft zu erheblichen numerischen Problemen (z.B. Wahl der Schrittweite, Handhabung nicht-differenzierbarer Stellen, usw.). Es gibt einen einfachen Trick, um alles das zu vermeiden: Iteratively Reweighted Least-Squares
Wir lösen dabei das System zunächst mit least-squares-Fehlerfunktionen \[E = \omega_i (f(x_i)-y_i)^2 \text{ mit } \omega_i=1.\] Danach hat man an jedem Punkt ein Residuum \[ r_i = f(x_i)-y_i \] Dieses nutzen wir, um die Fehlerterme neu zu gewichten. Für ein \(\ell_1\)-Fehler würden wir z.B. das Gewicht nun auf \[\omega_i = \frac{1}{r_i}\] setzen, und die Optimierung nochmal starten. Das wiederholen wir solange, bis sich nichts mehr ändert. In diesem Fall ist die Konvergenz zu einem globalen Minimum übrigens garantiert, aber man braucht u.U. relativ viele (hunderte) Iterationen, bis sich wirklich nichts mehr ändert (Tipp: Für reale Implementierungen sollte man nicht \(\frac{1}{r_i}\) sondern \(\frac{1}{r_i+\epsilon}\) für ein sehr kleines \(\epsilon>0\) benutzen, um Divisionen durch null, oder sehr-nahe-an-null, zu vermeiden; solche Punkte hätten dann unendliches Gewicht bzw. die Zielfunktion ist leider an dieser Stelle nicht differenzierbar, was uns die Numerik zerschießt.)
Man kann damit auch andere Fehlerfunktionen, wie das “Abschneiden” von Ausreißern, implementieren. In diesem Fall würde man in der nächsten Iteration den Fehler auf eine Konstante setzen, falls das Residuum einen bestimmten Wert überschreitet (das kann man natürlich auch mit \(\ell_1\) kombinieren).
Diese Methode ist prinzipiell sehr robust (im Sinne von numerisch robust - es ist eine robuste Methode um robuste Statistik zu implementieren :-) ) und einfach zu implementieren. Allerdings sind oft viele Iterationen erforderlich, so dass direkte Löser, die via eines Abstiegsverfahrens (Gradientenabstieg, Newton-Methode, l-BFGS oder ähnlichem) arbeiten, deutlich schneller sind (allerdings sehr viel schwieriger robust, im Sinne numerischer Robustheit, zu implementieren).
Man sollte hier die numerische Effizienz auch nicht überbewerten: In vielen Anwendungen spielt diese keine sehr große Rolle; die Fähigkeit auch mit nicht-normalverteilten Daten (vor allem mit Ausreißern) arbeiten zu können, tritt dagegen recht oft auf, und sobald man das Problem hat, ist es in der Regel ein existenziel wichtiges (da sonst z.B. wenige Ausreißer alles kaputt machen können).
Das zentrale Gegenargument gegen einfache numerische Optimierer (IRLS oder auch potentiell effizientere Abstiegsverfahren) ist, dass diese keine globalen Minima für nicht-konvexe Funktionale finden können. Für bestimmte Anwendungen ist aber gerade dies leider die Hauptherausforderung. Ein Beispiel siund regularisierte Stereovision-Rekonstruktionsprobleme - hier kommt man ohne globale Optimierungsverfahren nicht weiter (oder man nimmt halt tiefe Netze für alles, und lernt die Rekonstruktion, aber das ist eine andere Geschichte).
Aufgabe 4.1: Leiten Sie her, wie eine Ausgleichsgerade durch \(n\) Punkte \((x_1,y_1),...,(x_n,y_n)\) gelegt werden kann. Dabei sollen Fehler in \(y\) im least-squares-Sinne ausgeglichen werden.
Aufgabe 4.2: Die Methode der Normalengleichungen, die man z.B. in Aufgabe 4.1 typischerweise erhält, ist numerisch weniger stabil. Warum? Wie kann man das Problem vermeiden, indem man die Lösung “direkt” mit der Singulärwertzerlegung bestimmt? Erklären Sie, warum Ihre Lösung richtig ist! Letzte Teilfrage: Was sind potentielle Nachteile der SVD-Methode?
Aufgabe 4.3: Erklären Sie, wie man ein least-squares-Verfahren mit “iterated least-squares” robuster gegen Ausreißer (einzelne, sehr große Fehler) machen kann.
Vorweg: Die Prämisse dieses Kapitels ist strenggenommen nicht wahr. Wenn man die Augen zusammenkneift, sieht es aber fast so aus.
In diesem Kapitel geht es darum, wie man eine gute Basis für ein (lineares) Modellierungsproblem finden kann. Die Hauptachsenanalyse, und ihre Varianten, sind Methoden, die Koordinatensysteme berechnen können, die für bestimmte Aufgaben besonders gut geeignet sind.
Wenn wir es mit einem Problem aus der linearen Algebra zu tun haben, können sich prinzipiell zwei Fragen ergeben: - (A) Koordinaten aus Daten: Wir haben eine Menge von Datenpunkten \[ \mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d \] gegeben, und suchen ein Koordinatensystem, welches diese Punkte “besonders gut” darstellen kann. Das macht man mit Hauptachsenanalyse (PCA). - (B) Koordinaten aus linearen Abbildungen: Hier ist eine lineare Abbildung \[ \mathbf{M}: \mathbb{R}^{d_1} \rightarrow \mathbb{R}^{d_2} \] gegeben. Wir suchen ein Koordinatensystem, welches diese lineare Abbildung “besonders gut” darstellen kann. Das macht man mit der, bereits zuvor eingeführten, Singulärwertzerlegung (SVD), oder ihrem Spezialfall, der Diagonalisierung.
Wir werden sehen, dass diese beiden Konzepte eng verwandt sind. Außerdem gibt es verschiedene Arten, Problem (A) zu stellen (statt Punkte könnten hier auch Distanzen oder paarweise Skalarprodukte gegeben sein, z.B. im Rahmen eines Kernelalgorithmus).
Wenn man sich auf den Standpunkt stellt, dass (A) und (B) fast das gleiche sind (man kann dies mit ganz ähnlichen Algorithmen berechnen), dann ist fast alles PCA. :-)
Wie bekommen wir ein hübsches Koordinatensytem für gegebene Daten? Was könnten wir wollen? Im Prinzip ist das Koordinatensystem gut, wenn wir die gegebenen Punktmengen mit möglichst wenigen Koordinatenachsen bereits gut approximieren können.
Seien also im folgenden \[ \mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d \] \(n\) gegebene Datenpunkte im \(d\)-dimensionalen Raum. Wir können nun drei Probleme betrachten, die sich als äquivalent herausstellen:
(A1) Hyperebenenfitting: Wir möchten einen \(k\)-dimensionalen affinen Unterraum von
\(\mathbb{R}^d, 0 \leq k\leq d\)
finden, der diese Punkte möglichst gut approximiert. Für diesen Raum
möchten wir eine orthogonale Basis \(\mathbf{b}_1,...,\mathbf{b}_k \in
\mathbb{R}^d\) und einen Ursprung \(\boldsymbol{\mu} \in \mathbb{R}^d\) finden,
so dass
\[
\sum_{i=1}^n\operatorname{dist} \left(\boldsymbol{\mu} +
\operatorname{span}\{\mathbf{b}_1,...,\mathbf{b}_k\} , \mathbf{x}_i
\right)^2 \rightarrow min.
\]
so klein wie möglich wird (im least-squares Sinne). Wichtig: Die
Vektoren \(\boldsymbol{\mu},
\mathbf{b}_1,...,\mathbf{b}_k \in \mathbb{R}^d\) sind hier die
Unbekannten!
(A2) Dimensionsreduktion: Wir möchten die Punkte \(\mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d\) mit weniger Koordinaten darstellen, d.h., wir möchten sie durch Koordinatenvektoren \[\tilde{\mathbf{x}}_1,...,\tilde{\mathbf{x}}_n \in \mathbb{R}^k, k < d\] ersetzen, und dabei eine optimale Approximation (wieder im least-squares-Sinne) erhalten: \[ \sum_{i=1}^n \left(\tilde{\mathbf{x}}_i - \mathbf{x}_i \right)^2 \rightarrow min. \] Dabei sollen die Approximationen \(\tilde{\mathbf{x}}_i\) als linearkombinationen der Basisvektoren (mit Offset \(\boldsymbol{\mu}\)) dargestellt werden, d.h.: \[ \tilde{\mathbf{x}}_i = \boldsymbol{\mu} + \sum_{j=1}^k\lambda_j \cdot \mathbf{b}_j \text{ für optimal gewählte Koordinaten } \lambda_1,...,\lambda_k \in \mathbb{R} \] Insgesamt erhält man das Optimierungsproblem \[ \sum_{i=1}^n \left(\operatorname{arg\ min}_{\lambda_1,...,\lambda_k} \left[\boldsymbol{\mu} + \sum_{j=1}^k\lambda_j \cdot \mathbf{b}_j\right] - \mathbf{x}_i \right)^2 \rightarrow min., \] wobei wiederum die Vektoren \(\boldsymbol{\mu}, \mathbf{b}_1,...,\mathbf{b}_k \in \mathbb{R}^d\) die Unbekannten sind.
(A3) Hauptvarianzachsen einer maximum-likelihood-Normalverteilung bestimmen: In dieser Problemformulierung bestimmen wir zunächst Mittelwert \(\boldsymbol{\mu} \in \mathbb{R}^d\) und Kovarianzmatrix \(\boldsymbol{\Sigma} \in \mathbb{R}^{d \times d}\) so, dass \[ \prod_{i=1}^n \mathcal{N}_{\boldsymbol{\mu},\boldsymbol{\Sigma}}(\mathbf{x}_i) \rightarrow max. \] Dies ist die maximum-likelihood Schätzung einer Normalverteilung (man nimmt eine Normalverteilung, unter der das Produkt der Wahrscheinlichkeiten der Daten maximal wird; man kann sich vorstellen, dass dies die “plausibelste” ist, und für unendlich viele Daten kann man auch zeigen, dass die stochastisch gegen die richtige Lösung konvergiert.) Wir sind nun aber noch nicht fertig: Wir vermuten nun, dass die Normalverteilung nicht rund und symmetrisch ist, sondern eher elliptisch verzerrt. Dazu möchten wir weiter die Hauptachsen der Ellipse bestimmen (daher der Name: Hauptachsenanalyse, oder Principle Component Analysis = PCA). Diese Ergeben sich als orthogonale Koordinatentransformation, mit der man eine Einheits-Gauss-Ellipse verzerren müßte, um die vorgefundene Verteilung wirklich zu treffen. Formal stellen wir die Kovarianzmatrix dar als: \[ \Sigma = (\mathbf{U}\mathbf{D})^2 = (\mathbf{U}\mathbf{D}) \mathbf{D}\mathbf{U}^T = \mathbf{U} \mathbf{D}^2 \mathbf{U}^T, \] wobei \(\mathbf{U}\) eine orthogonale Matrix ist, deren Spalten genau den Hauptachsen entspricht, und \(\mathbf{D}\) eine Diagonalmatrix ist, auf deren Diagonale die Standardabweichungen stehen, d.h., die Eigenwerte von \(\Sigma\) sind die Varianzen \(\mathbf{D}^2 = \operatorname{diag}(\sigma_1^2,...,\sigma_d^2)\) der Daten.
Wenn man sich diese drei Probleme so anschaut, dann stellt man ziemlich schnell fest, dass (A1), das Fitten von Unterräumen, und (A2), die Reduktion der Dimension das gleiche Problem sind. Wenn der Unterraum gut paßt, dann kann man via \[ \tilde{\mathbf{x}}_i = \sum_{j=1}^k \lambda_j \mathbf{b}_j + \boldsymbol{\mu} \] eine niedrig-dimensionale Approximation mit den Koordianten \[ \lambda_j = \langle \mathbf{x}_i - \boldsymbol{\mu}, \mathbf{b}_j \rangle \] bestimmen (also einfach der Projektion auf die - orthogonalen - Achsen; dass man immer noch den Ursprung \(\boldsymbol{\mu}\) abziehen und wieder draufaddieren muss, macht es etwas unübersichtlich, aber nicht schwieriger).
Wunderbar. Wie bestimmt man nun das Koordinatensystem \(\boldsymbol{\mu}; \mathbf{b}_1,...,\mathbf{b}_n\)? In der Vorlesung haben wir (relativ langwierig, siehe Folien) hergeleitet, dass der Mittelwert der Daten \[ \boldsymbol{\mu} = \frac{1}{n} \sum_{i=1}^n \mathbf{x}_i \] optimal ist (das wäre für alle drei Probleme A1-A3 ziemlich naheliegend/plausibel), und dass die Eigenvektoren der Daten-Kovarianzmatrix \[ \boldsymbol{\Sigma} = \frac{1}{n-1} \sum_{i=1}^n \mathbf{x}_i \mathbf{x}_i^T \] die optimale Basis für alle drei Probleme bilden (letzteres ist eher unanschaulich, stimmt aber). Die so gewonnenen \(\boldsymbol{\mu},\boldsymbol{\Sigma}\) sind auch maximum-likelihood Schätzungen für die Mittelwert und Kovarianzmatrix einer Normalverteilung aus Daten; eine Beweisskizze findet sich z.B. in dem für die Vorlesung empfohlenen Lehrbuch Duda, Hart, Stork: “Pattern Classification, 2nd Edition” (Wiley 2001) auf Seite 88/89.
Der Algorithmus der Hauptachsenanalyse, auf Englisch “principal component analysis” oder kurz PCA berechnet die Lösungen zu den drei oben genannten Problemen. Er nimmt Beispielpunkte als Eingabe und arbeitet dann in drei Schritten:
Gegeben: Datenpunkte \[ \mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d \]
Algorithmus: Hauptachsenanalyse
Optional: Dimensionsreduktion
Anwendungen
Was kann man mit den Ausgaben der PCA machen? Hier sind ein paar Interpretationen der Ausgaben:
Optimalität der Kompression
Wir beweisen nun einige Eingeschaften bezüglich optimaler Approximationen, da man hier einige wichtige Strukturen und Eigenschften sieht, die man in der Praxis dauernt braucht:
Satz: Wenn man auf eine (irgendeine!) ortho-normale Basis \(\mathbf{u}_1,...,\mathbf{u}_d\) projiziert, und dabei einige Koeffizienten ausläßt, dann ist die Summe der quadratischen Fehlern genau die Summe der quadrate der ausgelassenen Koeffizienten.
Beweis: Seien \(\mathbf{u}_1,...,\mathbf{u}_d \in \mathbb{R}^d\) orthognoal, d.h. \[ \langle \mathbf{u}_i , \mathbf{u}_j \rangle = \delta_{i,j} \]
Sei weiterhin \(\kappa_i=1\), falls wir die \(i\)-te Koordinate speichern wollen, und \(\kappa_i=0\), falls wir sie unter den Tisch fallen lassen wollen. Damit können wir eine Kompression eines Vektors \(\mathbf{x}\) zu \(\tilde{\mathbf{x}}\) durch “weglassen” von Koordinatenn definieren:
\[ \tilde{\mathbf{x}} = \sum_{i=1}^d \kappa_i \underbrace{\langle \mathbf{x},\mathbf{u}_i \rangle}_{=:\lambda_i} \mathbf{u}_i = \sum_{i=1}^d \kappa_i \lambda_i \mathbf{u}_i \] (Die Koordinaten mit \(\kappa_i=0\) würden wir in einer praktischen Anwendung natürlich erst gar nicht berechnen/speichern.)
Offensichtlich ist das Residum \[ \mathbf{x} - \tilde{\mathbf{x}} = \sum_{i=1}^d \lambda_i \mathbf{u}_i - \sum_{\substack{i=1..d \\ \kappa_i=1}} \lambda_i \mathbf{u}_i = \sum_{\substack{i=1..d \\ \kappa_i=0}} \lambda_i \mathbf{u}_i \]
Der quadratische Fehler ist nun schlicht:
\[ \|\mathbf{x} - \tilde{\mathbf{x}}\|^2 = \langle \tilde{\mathbf{x}} - \mathbf{x}, \tilde{\mathbf{x}} - \mathbf{x} \rangle = \Big \langle \sum_{\substack{i=1..d \\ \kappa_i=0}} \lambda_i \mathbf{u}_i , \sum_{\substack{i=1..d \\ \kappa_i=0}} \lambda_i \mathbf{u}_i \Big \rangle \] \[ = \sum_{\substack{i=1..d \\ \kappa_i=0}} \ \ \sum_{\substack{j=1..d \\ \kappa_j=0}} \ \ \lambda_i \lambda_j \underbrace{\langle \mathbf{u}_i , \mathbf{u}_j \rangle}_{=\delta_{i,j}} \] \[ = \sum_{\substack{i=1..d \\ \kappa_i=0}} \lambda_i^2 \]
Anders gesagt: Wenn man eine orthogonale Basis hat, und man läßt Achsen bei der Kompression von Vektoren (also Projektion+Rekonstruktion) aus, dann ist das Quadrat des Fehlers (d.h., die quadratische Distanz zwischen Original und Fälschung) genau die Summe der Quadrate der weggelassenen Koordinaten \(\lambda_i = \langle \mathbf{x},\mathbf{u}_i\rangle\).
Anwendungsbeispiel: Dies kann z.B. für die Konstruktion von Bildkompressionsverfahren verwendet werden. Ein einfacher Ansatz ist es, ein Bild zunächst in eine orthogonale Basis zu transformieren, und danach die kleinsten Koeffizienten einfach wegzulassen.
Beliebt sind z.B.: - Die Haar-Wavelet-Basis. - Oder die patchweise Fourier-Basis. Hier führt man eine diskrete 2D Fouriertransformation, DFT, auf z.B. 8x8-Pixel-Patches des Bildes aus und komprimiert jeden Patch einzeln, indem man die kleinsten Koeffizienten auf Null setzt.
Nach der “Quantisierung” (hier Koeffizienten auf Null setzten; im allgemeinen kann es auch eine Genauigkeitsreduktion, d.h. Einsparung von einigen, aber nicht allen, Bits sein) kann man Standardkompressoren wie RLE und/oder Huffmankodierung verwenden, um das Bild wesentlich kompakter zu speichern. Mit den beiden o.g. Techniken kann man 1:10 Kompressionen mit mäßigem Verlust für natürliche Bilder/Photos erreichen. Richtig schicke Verfahren wie JPG (Fourier-Patches) oder JPG-2000 (Waveletbasiert) benutzen verfeinerte Basiskonstruktionen und Perzeptuell-optimierte Quantisierung (auch nicht nur auf 0/1), sowie ausgefeilterte Kompressoren als einfach nur Huffman+RLE. Für den Hausgebrauch reicht das aber vielleicht schon - will sagen, man sieht das Kernprinzip daran ganz gut.
Nun zu Teil 2: Fehler bei der Dimensionsreduktion
Satz: Die Dimensionsreduktion der PCA hat einen mittleren quadratischen Fehler, der der Summe Eigenwerte der ausgelassenen Dimensionen entspricht: \[\frac{1}{n} \sum_{i=1}^n \| \tilde{\mathbf{x}}_i-\mathbf{x}_i\|^2 = \sum_{i=K+1}^n\sigma_i^2\]
Beweisskizze: Wie zuvorgesehen, ist der quadratische Fehler für jedes einzelne \(\tilde{\mathbf{x}}_i\) genau die Summe der ausgelassenen Koeffizienten \[\| \tilde{\mathbf{x}}_i-\mathbf{x}_i\|^2 = \sum_{j=K+1}^n[\lambda_j^{(i)}]^2\] Wir betrachten nun erstmal jede Achse \(j=K+1...n\) einzeln: Der Erwartungswert dieses Fehlers in einer Achse \(j\) ist genau die (empirische) Varianz \(\sigma_j^2\) in diese Richtung. Die Summe der quadratischen Abweichungen über alle Achsen \(j\) und alle Vektoren \(i\) kann man umsortieren in die Summe über alle Vektoren \(i\) über jeweils alle Achsen \(j\) und enthält eentsprechend für die mittlere Summe der Fehler die Summe der Varianzen.
Was heißt das für die Praxis?
Wenn man nicht genau weiß, wie stark man bei einer PCA-Dimensionsreduktion komprimieren kann (also die Dimension reduzieren), dann kann man sich den Rest des Eigenwertspektrums (engl: “tail” of the spectrum) anschauen. Sobald die Restsumme \[ \sum_{i=K+1}^n\sigma_i^2 \] hinreichend klein ist (z.B. 10%, oder 1%, je nach Anwendung), dann kann man sich den Rest sparen.
Für manche Anwendungen ist der Gewinn, also die Zahl der Dimensionen, die man weglassen kann, enorm (Beispiel: das morphable Face Model), bei anderen widerum eher gering:
Es gibt einige interessante Varianten von PCA, die wir nun (nur kurz) diskutieren wollen.
“Duale PCA”
Soweit ich weiß, hat das Ding keinen Namen; ich nenne es daher so, weil man in einem gewissen Sinne Eingabe- und Ausgaberichtungen vertauscht.
Nehmen wir wieder an, dass wir Datenpunkte \[ \mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}^d \] betrachten (ich schreibe “betrachten”, weil wir sie vielleicht nicht explizit kennen; mehr dazu in kürze).
Wir nennen nun die (u.U. gedachte) “zentrierte Datenmatrix” \(\mathbf{X}\): \[ \mathbf{X} := \underbrace{ \left.\left( \begin{array}{ccc} \vert & & \vert \\ \mathbf{x}_{1} -\boldsymbol{\mu} & \cdots & \mathbf{x}_{n}-\boldsymbol{\mu} \\ \vert & & \vert \end{array} \right)\right\} }_{n \text{ Datenpunkte}} \scriptstyle d\text{ Dimensionen} \]
Zentriert bedeutet in diesem Zusammenhang, dass wir den Mittelwert der Daten bereits abgezogen haben.
Dann erhält man die Eigenvektoren der PCA durch Diagonalisierung der Kovarianzmatrix
\[ \boldsymbol{\Sigma}=\frac{1}{n-1}\mathbf{X}\mathbf{X}^T \]
Wenn man sich nur für die Hauptachsen \(\mathbf{u}_i\) unteressiert, kann man übrigens auch den Normalisierungsfaktor \(1/(n-1)\) weglassen; das ändert die Eigenvektoren nicht. In der Vorlesung hatten wir das als “Scattermatrix”
\[ \mathbf{S}=\mathbf{X}\mathbf{X}^T \] bezeichnet.
Die Duale PCA betrachtet statt der \(d \times d\) Kovarianzmatrix \(\boldsymbol{\Sigma}\) die \(n \times n\) “Grammatrix”
\[ \mathbf{G}=\mathbf{X}^T\mathbf{X} \]
Die beiden Matrizen haben die gleichen Eigenwerte. Um dies zu beweisen, schreiben wir \(\mathbf{X}\) formal in Singulärwertzerlegung: \[ \mathbf{X} = \mathbf{U} \mathbf{D} \mathbf{V}^T \] Dann ist \[ \mathbf{S} = \mathbf{U} \mathbf{D} \mathbf{V}^T \mathbf{V} \mathbf{D} \mathbf{U}^T = \mathbf{U} \mathbf{D}^2 \mathbf{U}^T \] und \[ \mathbf{G} = \mathbf{V} \mathbf{D} \mathbf{U}^T \mathbf{U} \mathbf{D} \mathbf{V}^T = \mathbf{V} \mathbf{D}^2 \mathbf{V}^T \]
Bemerkung: Wenn man mag, kann man die Grammatrix auch normalisieren: \(\mathbf{G}_n=\frac{1}{n-1}\mathbf{X}^T\mathbf{X}\) hätte dann genau das gleiche Eigenwertspektrum wie \(\boldsymbol{\Sigma}\).
Die Eigenvektoren sind nicht die gleichen: \(\mathbf{U}\) enthält direkt die Hauptachsen, \(\mathbf{V}\) enthält Faktoren für Linearkombinationen von Datenpunkten (also “duale Information”), die die Hauptachsen indirekt darstellen. Dies kann man aber zurückrechnen, falls man die Originaldaten \(\mathbf{X}\) kennt: \[ \mathbf{X} = \mathbf{U} \mathbf{D} \mathbf{V}^T \Rightarrow \mathbf{U} = \mathbf{X} \mathbf{V} \mathbf{D}^{-1} \]
Wozu ist das gut?
Drei Anwendungen:
SVD und PCA
Wie zuvor gesehen, sind SVD und PCA ebenfalls eng verwandt:
Kennt man also die SVD der Datenmatrix, so hat man die PCA gleich mit erledigt. Die Dimensionsreduktion von \(d\) auf \(k \leq d\) Dimensionen kann man durch Projektion auf die ersten \(k\) Spalten von \(\mathbf{U}\) oder durch “querlesen” der ersten \(k\) Eitnräge der mit den Singulärwerten skalierten rechtsseitigen Singulärvektoren \(\mathbf{D}\mathbf{V}^T\) erhalten.
Man kann sich auch vorstellen, dass man Datenpunkte \(\mathbf{x}_1,...,\mathbf{x}_n\) linearkombinieren möchte, um neue Datenpunkte aus dem selben Unterraum zu erzeugen. Die SVD analysiert diese lineare Abbildung, wie wir uns im nächsten Kapitel genauer anschauen.
Schauen wir uns nun das zweite Problem an: Wir haben in Kapitel 2.6 bereits gesehen, dass man jede lineare Abbildung (endlich-dimensional, oder mit etwas Aufwand auch auf bestimmten Funktionenräumen, die eine abzählbare Schauderbasis haben, wie z.B. dem Raum \(\ell_2\)) wie folgt darstellen kann:
\[ \mathbf{M} = \mathbf{U} \mathbf{D} \mathbf{V}^T \]
Dabei sind \(\mathbf{U,V}\) orthogonale Abbildugnen und \(\mathbf{D}\) ist diagonal. Für symmetrische Matrizen erhält man \(\mathbf{U}=\mathbf{V}\), und die Abbildung ist diagonalisierbar. Für das lösen linearer Probleme ist das optimal: wir bekommen eine Menge unabhängiger Gleichungen. Ein solches Koordinatensystem ist also für das Lösen von Problemen “das beste”.
Wir schauen uns nun zwei Beispiele an. Im ersten Fall besteht die Matrix \(\mathbf{M}\) wirklich aus Datenpunkten und im zweiten Fall handelt es sich um eine lineare Abbildung (potentiell unendlich-dimensional).
Viele Online-Dienste, die ihren Nutzern z.B. Produkte oder Medien empfehlen, nutzen Varianten der Singulärwertzerlegung dafür. Hier ein Beispiel:
In der Praxis hat man noch das Problem, dass nicht jeder der Kunden jeden Film anschauen wird, sondern wohl eher eine kleine Auswahl. Das bedeutet, dass die Matrix \(\mathbf{X}=[\mathbf{x}_1 | ... | \mathbf{x}_n]\) nicht voll besetzt ist, sondern (sehr viele) unbekannte Werte enthält. Eine SVD-Zerlegung mit unbekannten Werten zu berechnen, die immer noch eine least-squares-optimale Faktorisierung darstellt, ist leider ein NP-hartes Problem. Das macht aber nichts in dieser Anwendung, da eine “gute” Lösung gut genug ist - wir brauchen nicht das globale Optimum. Ein oft genutzter praktischer Algorithmus ist…
Alternating Least-Squares für Matrixfaktorisierung mit (vielen) unbekannten Werten
Wir bauen eine \(n \times k\) Matrix \(\tilde{\mathbf{V}}\) und eine \(k \times d\) Matrix \(\tilde{\mathbf{U}}\) und setzen: \[ \mathbf{X} \approx \tilde{\mathbf{U}} \cdot \tilde{\mathbf{V}}^T \] (Die Matrix \(\mathbf{D}\) können wir weglassen und in \(\tilde{\mathbf{U}}\) oder \(\tilde{\mathbf{V}}\) einbauen, indem wir die Spalten nicht normalisieren). Wir initialisieren nun beide Matrizen mit Zufallswerten und lösen ausgehend von dieser Initialisierung das Least-Squares Problem \[ \left\|\mathbf{X} - \tilde{\mathbf{U}} \cdot \tilde{\mathbf{V}}^T\right\|^2 \rightarrow min. \] abwechselnd mit \(\tilde{\mathbf{U}}\) oder \(\tilde{\mathbf{V}}\) als Unbekannter (und der anderen Matrix als fester Konstanten). Dies ist ein einfaches, lineares least-squares Problem (d.h., wir haben hier eine quadratische Zielfunktion). Nach jeder Iteration sorgen wir dafür, dass die Lösung orthogonalisiert wird (also die Spaltenvektoren der Matrizen ortogognal gemacht werden, z.B. mit einer SVD).
Zusammengefaßt
Wir haben uns hier vorgestellt, dass wir Datenpunkte linearkombinieren können/wollen, um neue Datenpunkte (gut) anzunähern. Wenn die SVD dieser linearen Abbildung niedrigen Rank hat (also nur wenige Singulärwerte im Betrag sich stark von \(0\) unterscheiden), dann ist dies möglich, und verrät uns etwas über die Daten. Im Videothekbeispiel oben ist der SVD-Ansatz eine natürliche Modellierung. Auch Hauptachsen von Punktwolken kann man so ansetzen (und es lohnt sich, von der Rechengeschwindigkeit, die SVD zu benutzen, wenn das Produkt \(n\times d\) nicht zu groß ist), aber hier ist die original PCA Formulierung wohl natürlicher.
Am Ende ist das alles (PCA, MDS, SVD) fast das gleiche.
Schauen wir nun zum Abschluß noch ein Beispiel an, bei dem der “Datensatz” ein linearer Operator ist, der in einer PDGL steckt. Auch hier kann man soetwas wie “PCA” machen:
Wir modellieren die Temperatur in einem Stück homogenen Materials, z.B. einer Metallplatte, als Funktion \[\begin{eqnarray} f:& &\mathbb{R}\times [0,1]^2 \rightarrow \mathbb{R} \\ f(t,\mathbf{x}) &=& \text{Temperatur an Ort } \mathbf{x} \text{ zum Zeitpunkt }t. \end{eqnarray}\]
Die Ausbreitung von Wärme mit der Zeit wird durch die partielle Differentialgleichung \[ \partial_t f(t,\mathbf{x}) = - \tau \Delta_\mathbf{x} f(t,\mathbf{x}) = - \tau \left(\partial_{x_1}^2 f(t,\mathbf{x}) + \partial_{x_2}^2 f(t,\mathbf{x})\right) \] beschrieben. Der Parameter \(\tau\) gibt dabei die Wärmeleitfähigkeit an - je größer, desto schneller gleichen sich Temperaturunterschiede aus.
Wir starten in einem Anfangswert \(f(0,\mathbf{x})\), der für \(t=0\) eine feste Wäreverteilung vorgibt. Danach zerfließt diese, bis alles eine mittlere Temperatur hat: Der Term auf der rechten Seite mit dem \(\Delta\) misst lokal, wie ungleichmäßig die Wärme verteilt ist (im Sinne der Abweichung des Wertes an der Stelle \(\mathbf{x}\) von seiner lokalen Umgebung) und gleicht diese mit der Zeit aus (die zeitliche Ableitung ist minus diese Abweichung vom Mittel).
Normalerweise braucht man fancy-Numerik, um dieses Problem zu lösen. Außer man kennt die richtige Basis: Man kann leicht nachrechnen, dass die Funktionen \[ \left(\begin{array}{c}x_1\\x_2\end{array}\right) \mapsto \exp\left(-2\pi i (k_1 x_1 + k_2 x_2)\right) \text{ für } k_1, k_2 \in \mathbb{Z}, \] auch bekannt als 2D-Fourierbasis, Eigenfunktionen von \(\Delta = \partial_{x_1}^2+\partial_{x_2}^2\) mit Eigenwerten \(k_1^2+k_2^2\) sind. Damit bekommt man ein Diagonalsystem. Nehmen wir an, wir nummerieren die Basisfunktionen durch als \(b_k\) und die Eigenwerte als \(\lambda_k\) für \(k\in\mathbb{Z}\) (z.B. indem wir das 2D-Koeffizientenarray spiralförmig von der Mitte nach außen durchnummerieren), dann vereinfacht sich die Gleichung zu \[ f(t,\mathbf{x}) = \sum_{k \in \mathbb{N}} b_k \lambda_k^t \cdot start_k \] mit \[ start_k := \langle f(0, \cdot ), b_k\rangle = \int_{[0,1]^2} f(0, \mathbf{x} ), b_k(\mathbf{x}) d\mathbf{x}. \] Der Grund ist (anschaulich) der folgende: Um einen Zeitschritt \(t\mapsto t+1\) zu machen, müssen wir den aktuellen Zustand (ungefähr, es gilt natürlich nur für sehr kleien Schritte exakt) mit \(-\tau\Delta\) multiplizieren. Wenn wir dies diagonalisieren können, dann erhalten wir für \(N\) Zeitschritte (wir nehmen an, dass die Maßeinheit so gewählt ist, dass die Schritte sehr kleine Zeitintervalle repräsentieren):
\[ \Delta^N = \left[\mathbf{U}\mathbf{D}\mathbf{U}^T\right]^N = \mathbf{U}\mathbf{D}\mathbf{U}^T \cdots \mathbf{U}\mathbf{D}\mathbf{U}^T = \mathbf{U}\mathbf{D}^N\mathbf{U}^T \] Dies stimmt, weil \(\mathbf{U}\) orthogonal ist, also \(\mathbf{U}^{-1} = \mathbf{U}\).
Die Matrix \(\mathbf{D}\) enthält aber lediglich die Eigenwerte \(\lambda_k\): \[ \mathbf{D} = \left(\begin{array}{ccc} \lambda_1 & & \\ & \lambda_2 &\\ & & \ddots \\ \end{array}\right) \] Daher ist \[ \mathbf{D}^N = \left(\begin{array}{ccc} \lambda_1^N & & \\ & \lambda_2^N &\\ & & \ddots \\ \end{array}\right). \] Man kann sich überlegen (wir lassen das hier aus), dass dies auch im kontinuierlichen Grenzwert gilt, also \[ (\tau \Delta)^t = \mathbf{U} \mathbf{D}^t \mathbf{U}^T, \] und damit kann man die Lösung direkt hinschreiben (es sieht nur etwas komisch aus, da wir mit einer abzählbar-unendlichen Basis arbeiten müssen, wenn wir über eine “echte”, kontinuierliche Differnzialgleichung reden; man kann sich aber gerne alles als Matrizen und alle Schrite als 1er-Schritte in der Zeit vorstellen).
Fazit: Probleme können wesentlich einfacher werden, wenn man das richtige Koordinatensystem wählt. Für lineare (P)DGL ist dies eigentlich immer die Fourierbasis, da diese die Eigenfunktionen von linearen Differenzialoperatoren sind (wenn wir im Komplexen rechnen, was man ohne Bedenken tun kann; die Lösungen bleiben trotzdem reell).
Aufgabe 5.1: Erklären Sie (mit Herrleitung), warum (und in welchem Sinne) SVD, PCA und MDS, angewandt auf eine Punktwolke \(\mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}\) die gleichen Ergebnisse liefern.
Aufgabe 5.2: Erklären Sie, wie man mit PCA eine Ausgleichsebene in eine Punktwolke \(\mathbf{x}_1,...,\mathbf{x}_n \in \mathbb{R}\) im total-least-squares-Sinne legt.
Aufgabe 5.3: Wie kann man das Verfahren aus Aufgabe 4.2 mit einem iterative-reweighted-least-squares-Verfahren robust gegen Ausreißer machen? (Einzelne, weit entfernte Punkte sollen die Auslgeichsebene weniger stark beeinflussen.)
Aufgabe 5.4: Sie sind Chef eines Supermarktes. Sie haben Ihren Kunden eine Kundentruekarte untergejubelt, mit Hilfe derer Sie die Einkäufe Ihrer \(n\) Kunden genau tracken können. Sie haben folgende Daten: Für jeden Kunden die Menge an Produkten, die sie/er im laufe des letzten Jahres gekauft hat, aufgeschlüsselt nach allen \(k\) Produktkategorien, die Ihr Supermarkt führt (es sind mehrere 1000 Kunden und mehrere 10000 Produktkategorien). Die Marketingabteilug glaubt, dass es eigentlich nur drei Typen von Kunden gibt, die immer die gleichen Sachen kaufen (nur in unterschiedlichen Mengen). Wie können sie mit einem Datenanalyseverfahren feststellen, ob diese Hypothese stimmt?
Aufgabe 5.5: Immer noch der selbe Supermarkt: Was machen Sie, wenn sie nur tägliche Daten der Kunden haben, bei der viele Einkäufe, die sich über das Jahr ergeben haben fehlen (die Kunden sind auf den Dreh gekommen, dass Sie mit der Kundenkarte getrackt werden, und haben diese abgelehnt; sie kennen also nur tageweise Einzelkäufe, keine Jahresstatistiken). Kann man trotzdem ein solches Muster finden/berechnen?
Tipp: Schauen Sie sich vorab das Video von 3brown1blue über die Fourierreihen an. Das macht vieles wesentlich anschaulicher.
Diese Kapitel ist noch unvollständig. Eine sehr genaue Diskussion findet sich im (empfohlenen) Buch Principles of Digital Image Synthesis von A. Glassner im Abschnitt II “Signal Processing”.
Die Funktion \[ t \mapsto e^{-it} = i \sin(t) + cos(t), \ \ \ \ t \in [0,2\pi] \] beschreibt eine kreisförmige Kurven in der komplexen Ebene \(\mathbb{C}.\)
Wir betrachten die komplexe Fourierbasis \[ B_{\text{Fourier}} = \left\{ e^{-ikt} \mid k \in \mathbb{Z} \right\} \] Dies ist eine Schauderbasis für \(L_2([0,2\pi] \rightarrow \mathbb{C})\), also der Funktionen vom Interval \([0,2\pi]\) in die Komplexenzahlen als Hilbertraum \(L_2\). Anders gesagt: Alle sinnvollen Funktionen, die einem in der Physik (read: this universe) über den Wege laufen können, kann man damit (im Sinne der Standardintegralnorm) beliebig gut annähern.
Mehr brauchen wir also nicht (auf dem Intervall).
Man kann das ganze auch rein reell machen, mit einer Basis $ { (kx), (mx) k ^{>0}, m ^{} }$ und \(L_2([0,2\pi] \rightarrow \mathbb{R})\).
Wir beschränken uns auf den komplex Fall, aus Bequemlichkeit.
Die Koeffizienten erhält man einfach durch Projektion, da die Basis orthogonal ist:
\[z_k = \langle f, b_i\rangle = \int_0^{2\pi} f(x) b_k(x) dx\]
Die Rekonstruktion erfolgt analog als Summe von Basisfunktionen:
\[f(x) = \sum_{k=-\infty}^\infty z_k b_k(x)\]
Da die Sache konvergiert (Schauderbasis) kann man bei einem endlichen \(|k|\) abschneiden, ohne dass der Fehler zu groß wird. Wo man abschneiden kann, hängt von der Funktion \(f\) ab, die man annähern möchte.
Wir können versuchen, das Intervall zu ändern. Ist nicht schwer: \[ B_{[0,T]} = \left\{ \frac{1}{Z} e^{-ik\frac{2\pi t}{T}} \mid k \in \mathbb{Z} \right\} \] wobei \(1/Z\) so gewählt werden muss, dass für die Basisfunktionen gilt \(\|b_i\|=1\) (ich spare mir die genaue Berechnung.)
Der Witz ist das \(1/T\) im Nenner im Exponenten: Wenn man das intervall breiter macht, muß man die Frequenzen \(k/T\) immer dichter anneinander legen. Im Grenzwert erhält man die Fouriertransformation: \[F(\omega) = \langle f, b(\omega)\rangle = \int_\mathbb{R} f(x) e^{-i\omega x} dx,\] die eine Funktion als Ergebnis hat. Aus dieser kann man invers zurücktransformieren via \[f(x) = \langle b(x), F\rangle = \int_\mathbb{R} F(\omega) e^{i\omega x} d\omega.\]
Die Transformation ist praktischer, da man kein Intervall fixieren muss. Allerdings gibt es einige konzeptionelle Probleme, wenn man genau definieren möchte, welche Funktionen man hier transformieren darf (so dass alles auch wirklich konvergiert). Wir ignorieren dies im folgenden komplett (wobei einiges an notwendiger Theorie unter den Tisch fällt).
Im Computer gibt es nur die diskrete Fouriertransformation. Hierbei startet man mit der Fourierreihe aus Abschnitt 6.1 (die Transformation gibt es nicht in digital, da es kein echtes Kontinuum gibt; trotzdem nennt man das dann die “diskrete Fouriertransformation”. Hmmmm.)
Wir werten diese Basis nun wie folgt aus: - Wir nutzen die ersten \(k=-K...K\) Basisfunktionen. - Wir arbeiten mit den regulären Abtastpunkten \[x= 0,\frac{1}{K},\frac{2}{K},...,\frac{2\pi}{K}\] aus dem Intervals \([0,2\pi]\). - Wir werten alle Funktionen nur an diesen Punkten aus. D.h., wir betrachten nur Arrays der Länge \(K+1\).
Auch in dieser diskreten Fassung erhalten wir eine orthogonale Basis des - nun endlich-dimensionalen - Vektorraums \(\mathbb{C}^{K+1}\). Man sieht dies am einfachsten, indem man sich die Symmetrie der Kreisfunktion \(t \mapsto e^{-it}\) nochmal vorstellt; auch nach der Diskretisierung heben sich z.B. Integrale (Summen) über gemischte Terme weg. Auch die weiteren Eingenschaften (Faltungssatz etc.) bleiben hier erhalten.
Die Faltung von zwei Funktionen ist wie folgt definiert: \[[f \otimes g](t) := \int_\mathbb{R} f(x) g(t-x) dx\]
Für die Fouriertransformation \(FT\) (als Operation auf Funktionen) gilt: \[ FT(f \otimes g) = F \cdot G \] und umgekehrt: \[ FT(f \cdot g) = F \otimes G \] Die gleichen Sätze gelten für die inversen Fouriertransformationen, wie auch alle analogen Konstruktionen (Fourierreihe, DFT) in analoger Weise.
Mit Hilfe des Faltungssatz kann man zeigen, dass Funktionen genau dann exakt aus einer diskreten Abtastung mit Abstand \(T\) bzw. Abtastfrequenz \(1/T\) wiederhergestellt werden können, wenn die Fouriertransformation der Funktion keine Frequenzen oberhalb der Nyquestfrequenz \(\nu = \frac{1}{2T}\) enthalten (man sagt auch, die Funktion ist band-beschränkt mit Frequenz \(\nu\)).
Sind höhere Frequenzen im Mix, dann erhält man Aliasingartefakte, d.h., man sieht niederfrequente Moirees in der Abtastung.
Bei der Rekonstruktion passiert etwas ähnliches: Man sollte Linearkombinationen von entsprechend band-beschränkten Funktionen nutzen. Siehe Vorlesung (oder das Buch von Glassner) für weitere Details.
Man kann die Theorie sinngemäß auch für irreguläre Abtastung benutzen, wenn man die Bandbeschränkungen und Tiefpaßfilter z.B. für so etwas wie den “mittleren Abstand” der Abtastpunkte nutzt. Der Hintergrund hierzu ist sehr ausführlich im genannten Buch von Glassner diskutiert.
Aufgabe 6.1: Wie entsteht Aliasing und welche Arten davon gibt es?
Aufgabe 6.2: Berechnen Sie die Fourier-Reihe für die Box-Funktion!
Aufgabe 6.3: Berechnen Sie die Fourier-Transformation für die Dreiecks-Funktion! Tipp: Die Boxfunktion hat \(\operatorname{sinc}(\omega)\) als Fouriertransformierte.
Aufgabe 6.4: Beweisen Sie den Faltungssatz für die Fouriertransformation!
In der Variationsrechnen macht man im Prinzip das gleiche wie im Least-Squares Kapitel, nur mit Funktionen als Unbekannten, und Funktionalen Gleichungen/Bedingungen als zusätzlichen Modellierungswerkzeugen (nicht nur vorgeschriebenen Werten).
Grob kann man in drei Schritten vorgehen:
Nehmen wir an, wir haben eine (lineare) Funktionalgleichung \[ L f = g \] Dabei ist \(L\) ein linearer Operator auf der Funktion \(f\), z.B. bei der Wärmeleitungsgleichung ist \(L=\partial_t-\Delta_\mathbf{x}\) für Funktionen \(f(\mathbf{x},t), f:\mathbb{R}^2 \supset \Omega \times \mathbb{R} \rightarrow \mathbb{R}\).
Wir können diese Gleichung vielleicht nicht direkt Lösen (z.B. weil das Definitionsgebiet \(\Omega\) kein Rechteck ist, und wir deshalb die passende Fourierbasis (die es für jedes sinnvolle \(\Omega\) prinzipiell gibt) nicht kennen). Noch schlimmer ist es, wenn \(L\) nicht diagonalisierbar ist, oder gar nicht-linear.
Dann versuchen wir das ganze approximativ: Wir bauen uns eine Basis \[ B = \{b_1,...,b_k\} \] von Basisfunktionen und nähern \[ f\approx \tilde{f} = \sum_{i=1}^K \lambda_i b_i \] Super. Nun ist das Lösen kein Problem. Wenn wir keinen richtige Mathemaitkvorlesung besuchen (tun wir gerade nicht), können wir ganz forsch versuchen, das \(\tilde{f}\) einfach in die Gleichung einzusetzen: \[ L \tilde{f} = g \] Das wäre ein LGS in \(K\) Unbekannten. Problem gelößt.
Mist - leider hat das Ding in der Regel keine Lösung, da der von der Basis aufgespannte Unterraum nicht unbedingt die korrekten Lösungen enhalten muß (nutzt man die Standardtricks, wie die B-Spline Basis, dann ist es eher unwahrscheinlich, dass das zufällig paßt).
Naja, das soll uns nicht aufhalten; versuchen wir least-squares:
\[ \|L \tilde{f} - g \|^2 \rightarrow min. \]
Das ist nun wirklich ein \(K \times K\) LGS (oder nichtlineares GS, falls \(L\) nicht linear war) das wirklich immer mindestens eine Lösung hat. Wir lösen dies mit einem geeigneten Löser (z.B. conjugate Gradients, was gut klappt bei DGL, also Differentialoperatoren \(L\), die schön sparse, also dünnbesetzt, sind.)
Wenn wir noch Randbedingungen haben, in der Form \(f(x)=y(x)\) für \(x \in R\), dann schreiben wir das einfach dazu:
\[ \|L \tilde{f} - g \|^2 + c \cdot \int_{x\in R}\| f(x) - y(x) \|^2 dx \rightarrow min. \] Immer noch least-squares, immer noch lösbar. Der Faktor \(c\) gibt an, wie stark wir Restfehler bei den Randbedingungen (vs. Residuum in der Funktionalgleichung selbst) bestrafen.
Da alles least-squares ist, kann man nun ohne Probleme die Randbedingungen durch Beobachtungen aller Art ersetzen, z.B. mit einem Term \[\sum_{m=1}^M \| f(x_m) - y_m \|^2\] für gemessene Werte \(y_m\) an der Stelle \(x_m\). Auch die Beobachtung differentieller Eigenschaften (Ableitungen oder auch Integrale) kann damit leicht als zusätzliche Information einfließen.
Es ist ein bischen der Weihnachtsmanalgorithmus: Wir schreiben alle unsere Wünsche auf, und der Optimierer (das wäre der WM) versucht, diese soweit wie möglich (mit dem durch \(B\) aufgespannten Unterraum) zu erfüllen.
Die Gleichungen \(Lf=g\) sind oft physikalische Gesetze (oder andere Gesetzmäßigkeiten aus empirischen Wissenschaften). Es gibt aber auch den Fall der rein regularisierenden Gleichungen. Wir können z.B. Bilder entrauschen, oder Tomographi-Rekonsturktionen regularisieren, indem wir eine Glattheitsbedingunge formulieren: Sei hierzu \[f:\mathbb{R}^2\rightarrow \mathbb{R}\] ein Bild, dann können wir ansetzen: \[ \operatorname{dist}(\text{Beobachtung}, f)^2 + c \cdot \|\nabla f\|^2 \rightarrow min. \] um eine Rekonstruktion zu erhalten, die möglichst genau die Beobachtungen erklärt, aber dabei vermeidet, zu große Gradienten zu haben (also wenig glatt zu sein).
Solche Regularisierungsfunktionale werden sehr häufig für die Rekonstruktion aus Beobachtungen benutzt, die nicht die zuverlässig volle (Bild-)information ergeben (z.B. Computertomographie), wo also die reine Erklärung der Beobachtung ein schlecht gestelltes Problem ist.
PS: In dem obigen Fall kann man übrigens leicht sehen, dass der Strafterm lediglich hohe Frequenzen bestraft: Die (1D) Fourierbasisfunktion \(e^{-ikt}\) ist eine Eigenfunktion der Ableitung, mit Eigenwert \(k\) (höhere Frequenzen werden also stärker bestraft). Die gleiche Konstruktion ist auch für 2D und höhere Dimensionen möglich.
Weitere Beispiele für Variationsansätze finden sich in den Vorlesungsfolien.
Aufgabe 7.1: Erklären Sie den Zusammenhang zwischen der harmonischen Energie und der Laplacegleichung \(\Delta f = 0\).
Aufgabe 7.2: Stellen Sie sich vor, wir haben von einem Bild (schwarz-weiss Photo als Pixelbild) nur die Gradienten (diskret an jedem Pixel) gegeben. Wie kann man daraus wieder ein Photo rekonstruieren? Betrachten Sie zunächst das kontinuierliche Problem, und stellen Sie eine Variationsgleichung auf. Wenden Sie dann die Euler-Lagrange-Gleichung an, um eine PDGL für die Lösung zu erhalten. Diskutieren Sie danach, wie man das (ungefähr) in Software lösen könnte. Hinweis: Das ist tatsächlich ein sehr praktisches Tool für fortgeschrittene Bildverarbeitungstechniken. Die Idee ist als “Gradient-Domain Image Editing” bekannt geworden. Hier ist das Originalpapier dazu.