Modellierung 1

Etwa 5 Euro.

Kapitel 6:

Kleinste Quadrate

Die Gaußsche Normalverteilung

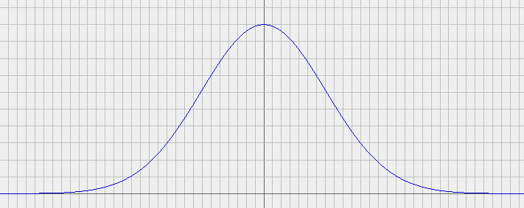
Als erstes schauen wir uns an (oder wiederholen) wie die multi-variate Gaußsche Normalverteilung definiert ist. Die verschiedenen Least-Squares-Approximationsalgorithmen (ehrlich gesagt, eigentlich alle quadratischen Optimierungsansätze) laufen nämlich alle darauf hinaus, die maximale Wahrscheinlichkeitsdichte einer entsprechenden Normalverteilung auszurechnen.

Video: Die (multivariate) Gaußsche Normalverteilung (20 min)

groß (3360x1080 mit Folien), mittel (1920x1080), klein(853x480), Folien (PDF)
Videos auf Panopto (Mirror)

Weiterführende Links: - https://de.wikipedia.org/wiki/Normalverteilung - https://de.wikipedia.org/wiki/Mehrdimensionale_Normalverteilung

Nachbereitung:

Multiplizieren Sie zwei Gaußsche Normalverteilungen mit beliebiger Varianz und Standardabweichung. Was ist die neue Wahrscheinlichkeitsdichte?
Nehmen Sie zwei 1D-Normalverteilungen (\(\sigma=1, \mu=0\)) und bauen Sie daraus die 2D-Normalverteilung via “Tensorprodukt”-Konstruktion (der Name ist wesentlich beeindruckender als die Rechnung). Warum ist das Ergebnis symmetrisch in dem Sinne, dass die Verteilung in jedem orthogonalen Koordinatensystem gleich aussieht (also drehsymmetrisch)?

Interpolation

Zur Vorbereitung auf die Least-Squares-Fitting Ansätze schauen wir uns nochmal kurz die Interpolation von Punkten mit einem linearen Funktionenansatz an. Der Stoff sollte prinzipiell aus der Schule bekannt sein (hier ist es nur etwas allgemeiner formuliert). Außerdem bashen wir noch etwas die Polynome. Die sind nämlich eigentlich (=bei hohem Grad) eher doof.

Video: Interpolation von Datenpunkten (15 min)

groß (3360x1080 mit Folien), mittel (1920x1080), klein(853x480), Folien (PDF)
Videos auf Panopto (Mirror)

Nachbereitung:

Fitten Sie per Hand, auf einem Blatt Papier, eine Parabel an drei Punkte in 1D. Rechnen Sie z.B. das Beispiel auf den Folien (Seite 10) nochmal selbst nach.

Least-Squares Approximation

Nun kommt das eigentliche Kernstück: Wir versuchen eine Menge von Punkten (Paare von Ein- und Ausgaben einer Funktion) durch eine Funktion anzunähern, und zwar so, dass die neue Funktion möglichst nahe an all diesen Punkten verläuft. Sollte dies nicht möglich sein, so wird eine Lösung bestimmt, die die Quadrate der Abstände (im Ausgaberaum) minimiert. Dabei wird die Approximationsfunktion als eine Linearkombination von Basisfunktionen gewählt (die grüne Wiese lässt grüßen). Es wird auch gezeigt, dass dieses Modell auf der Annahme basiert, dass die Fehler unabhängig und Normalverteilt sind - in dem Fall wird eine “Maximum-Likelihood Schätzung” erstellt. (Eine ML-Schätzung ist rekonstruiert asymptotisch die richtige Funktion mit immer höherer Wahrscheinlichkeit falls diese genau so eine Linearkombination ist, und die Anzahl der Samples immer weiter gesteigert werden kann).

Video: Die Least-Squares Methode zur Approximation von Datenpunkten (38 min)

groß (3360x1080 mit Folien), mittel (1920x1080), klein(853x480), Folien (PDF)
Videos auf Panopto (Mirror)

Nachbereitung:

Nehmen Sie an, Sie messen einen Wert \(x\) mehrmals, mit normalverteiltem Fehler. Die Messwerte Seien \(x_i\), und die Verteilungen haben konsistente Mittelwerte \(\mu_i = x\), aber schwankende Standardabweichungen \(\sigma_i\). Was ist die maximum-likelihood Rekonstruktion für das (unbekannte) \(x\) aus den (gemessenen) \(x_i\)s?

Wider dem Fehlerkommunismus – robuste Schätzer

Falls Fehler nicht normalverteilt sind, kann einiges schiefgehen. Hier schauen wir uns einige Techniken an, mit denen man Approximationsverfahren robust gegen Ausreißer und andere “heavy-tail”-Verteilungen machen kann. Eine (nicht besonders schnelle aber) einfache Implementation ist “Iteratively Reweighted Least-Squares (IRLS)”. Was so ähnlich klingt wie die amerikanische Bundessteuerbehörde beschreibt schlicht ein wiederholtes Fitting, bei dem die Gewichte schrittweise so angepasst werden, dass Ausreißer ein geringeres Gewicht bekommen als gut-passende Datenpunkte.

Video: Robuste Schätzer und IRLS (15 min)

groß (3360x1080 mit Folien), mittel (1920x1080), klein(853x480), Folien (PDF)
Videos auf Panopto (Mirror)

Gesamtlaufzeit Videos: 88min

Übungsaufgaben: Das fünfte Übungsblatt finden Sie hier: Modellierung-WS-22-23-Blatt-6.pdf. Die dazu gehörenden Materialien (70MB) finden sie hier: Modellierung-WS-22-23-Blatt-6.zip Datei wird Freitags bereitgestellt.)

Hinweis: Klicken Sie auf diesen Link, um auf die Panopto-Seite zu gelangen. Hier finden Sie alle Videos im mp4-Format für alle Geräte.

Datenschutz Impressum