Modellierung 1

Kapitel 4:

Jede Matrix hat so ihre eigenen (oder singulären) Werte

Kern, Bild, Dimensionsformel für lineare Abbildungen

Der exakte Fall: Man kann die Dimensionen abzählen.

Nachbereitung:

• Schauen Sie sich nochmal Ihre Vorlesungsunterlagen aus den Grundvorlesungen an zu:
  • Linearen Abbildungen
  • Matrix-Vector-Multiplikation
  • Matrix-Matrix-Multiplikation
  • Kern und Bild linearer Abbildungen
  • Dimensionsformel
  • Wie löse ich ein lineares Gleichungssystem mit Gaußelimination?
• Frage: Wie kann ich den Kern einer (durch eine Matrix dargestellte) linearen Abbildung konkret ausrechnen (z.B. mit einem modifizierten Gaussalgorithmus)?

Eigenwerte, Singulärwerte und Matrixfaktorisierungen (Diagonalisierung, SVD)

Eigenwerte und Singulärwerte.

Nachbereitung:

• Schauen Sie sich nochmal genau die Definition von Eigenwerten und Eigenvektoren an.
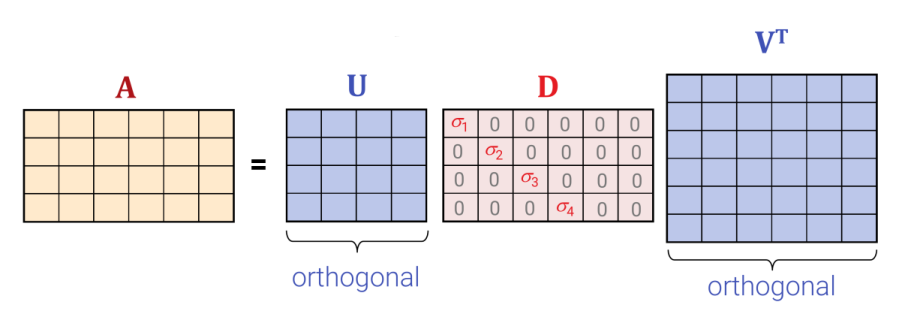
• Wie löse ich ein lineares Gleichungssystem \(\mathbf{A}\mathbf{x}=\mathbf{b}\), wenn ich die Singulärwertzerlegung \(\mathbf{A}=\mathbf{U}\mathbf{D}\mathbf{V}^T\) kenne?
• Die Matrix \(\mathbf{A} \in \mathbb{R}^{2\times 2}\) sei nun symmetrisch. Wie löse ich das Matrixgleichungssystem \(\mathbf{A}^2-3\mathbf{A} + 2\mathbf{I} = \mathbf{0}\)?
  Tipp: \(x^2-3x+2 = (x-2)(x-1)\).

Inverse Probleme

Der approximative Fall: Manche Dimensionen (Unterräume) lohnen sich nicht.

Nachbereitung:

• Nehmen wir an, das lineare Gleichungssystem \(\mathbf{A}\mathbf{x}=\mathbf{b}\) mit einer symmetrischen und positiv-definiten (alle Eigenwerte > 0) Matrix \(\mathbf{A}\) ist ein schlecht gestelltes Problem im Sinne der Vorlesung. Zeigen Sie, dass das Problem nicht mehr schlecht gestellt ist, wenn man \(\mathbf{A}\) durch \(\mathbf{A} +\epsilon \mathbf{I}\) für ein hinreichend großes \(\epsilon > 0\) ersetzt (die Lösung verändert sich dabei natürlich auch). Dies ist eine einfache Regularisierungstechnik für LGS aller Art. (Ein Trick nötig – Tipp: Eigenwertzerlegung)
• Warum ist der Ableitungsoperator \(d/dx\), der einer Funktion ihre Ableitung zuordnet, also \(f \mapsto f'\), (anschaulich) schlecht gestellt (ill-posed)?
• Wie ist die Situation bei der Integration, also \(f \mapsto F(x) := \int_0^x f(t) dt\) für (integrable) Funktionen \(f: [0,1] \rightarrow \mathbb{R}\)?

Quadratische Funktionen und Formen

Nicht-lineare lineare Algebra. Trotzdem nützlich.

Nachbereitung:

• Was ist der Unterschied zwischen (reine Begriffsklärung, Definitionen nochmal zusammentrage und vergleichen):
  • Quadratischen Formen
  • Quadriken
  • Quadratischen Polynomen (multi-variaten Polynomen mit totalem Grad 2)
• Wie schreibe ich ein allgemeines multi-variates quadratisches Polynom in Matrix-Vektor-Notation (gemeint sind die mit totalem Grad 2, alles andere interessiert uns in dieser Vorlesung nicht)?
• Warum können wir ohne Einschränkungen annehmen, dass die Matrizen einer quadratischen Form immer symmetrisch sind?
• Warum ist das toll? Will sagen: Was sagt uns das über die Struktur der quadratischen Polynome?

Gesamtlaufzeit Videos: 71min

Hinweis: Klicken Sie auf diesen Link, um auf die Panopto-Seite zu gelangen. Hier finden Sie alle Videos im mp4-Format für alle Geräte.

---