JGU Logo JGU Logo JGU Logo JGU Logo

Institut für Informatik

Michael Wand
David Hartmann
Sommersemester 2020 • DIGITAL

Blatt 11

Projektaufgabe
Einführung in die Softwareentwicklung



Exkurs: Compilerbau in 10 Minuten

Letzte Änderung: 29. June 2020, 10:47 Uhr
keine Punkte — im Detail
Ansicht:   |  


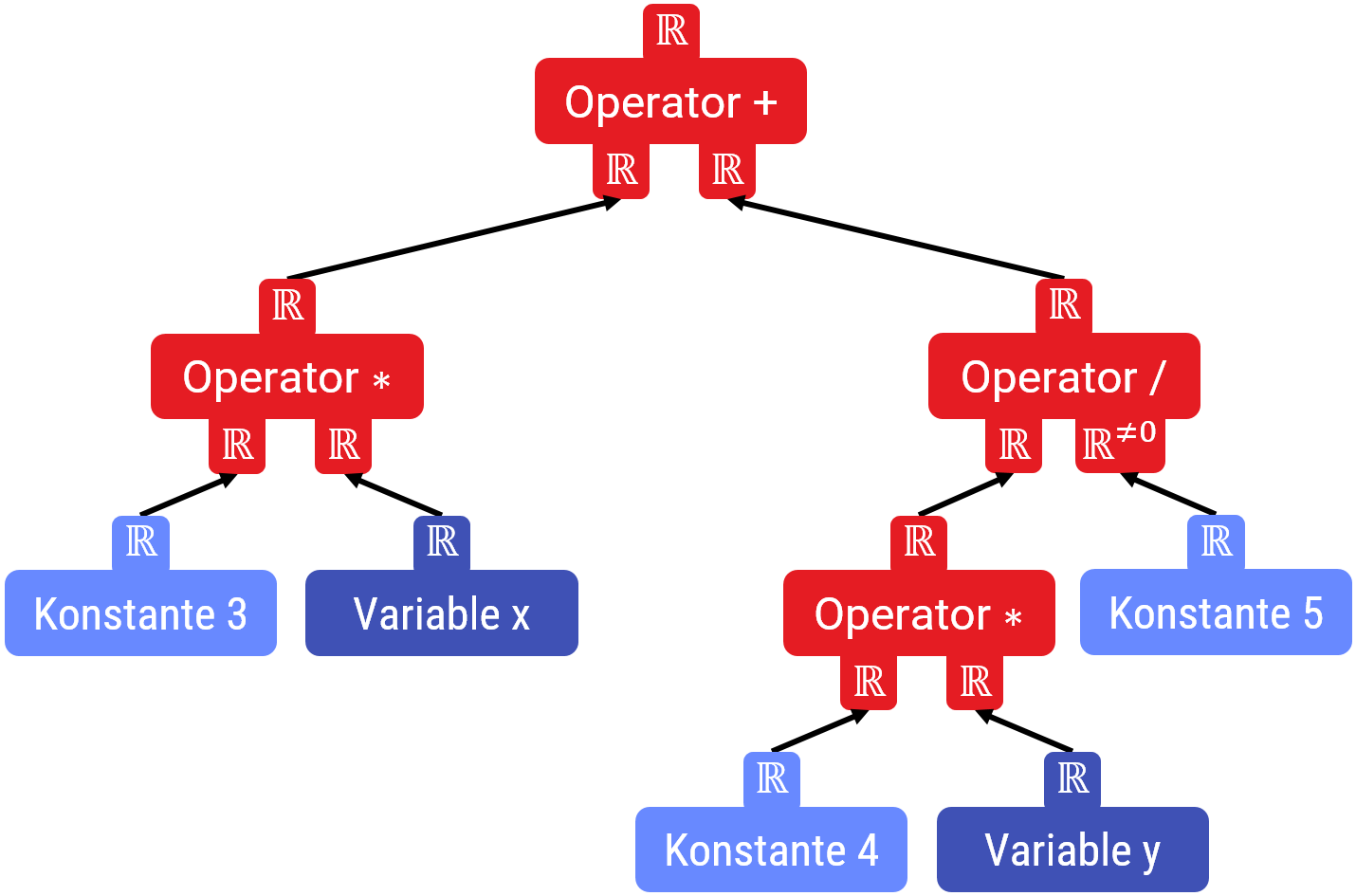
Kontextfreie Grammatiken beschreiben die Schachtelung von Bausteinen
Fast alle Programmiersprachen benutzen kontextfreie Grammatiken. Das heißt, dass das Programm aus Bausteinen besteht. Jeder Baustein ist ein Platzhalter: Er besteht aus einem gewissen Anteil an festem Text sowie weiteren Platzhaltern (wie ein Baum von Objekten in einer OOP-Sprache: Zeiger auf Unterobjekte müssen einen bestimmten Typ (Oberklasse) haben; welche Teilbäume man einsetzt ist aber egal, solange der Typ des direkt eingesetzten Typen stimmt.).


Die folgende Abbildung zeigt ein Beispiel für eine kontextfreie Grammatik: Die Bausteine sind mit spitzen Klammern markiert und werden mit dem Pfeil-Operator definiert. Auf der rechten Seite steht, mit welcher Folge von weiteren Bausteinen und/oder Zeichen, man einen Baustein ausfüllen kann. Dies macht man, bis alle Lücken (Platzhalter für Bausteine) gefüllt sind:


Abbildung 1: Eine Kontextfreie Grammatik besteht aus Bausteinen, die Knoten des Baumes entsprechen (hier mit spitzen Klammern und in Farbe markiert). Jeder Baustein kann konkrete Zeichen (grau) oder, hierarchisch geschachtelt, wieder andere Bausteine. Alle Möglichkeiten sind mit Pfeilen aufgelistet; einzelne Varianten mit dem oder-Operator (Hochstrich).


Der Parser hat nun die Aufgabe, aus einer gegebenen Zeichenkette (hier sind die Bausteine nicht mehr direkt ersichtlich) zu rekonstruieren, welcher Baum von Bausteinen (also, welche aufeinanderfolgende Ersetzung von Platzhaltern mit rechten Seiten der Pfeile, bis keine Platzhalter für Bausteine mehr übrig sind) zu der Zeichenkette gehört:


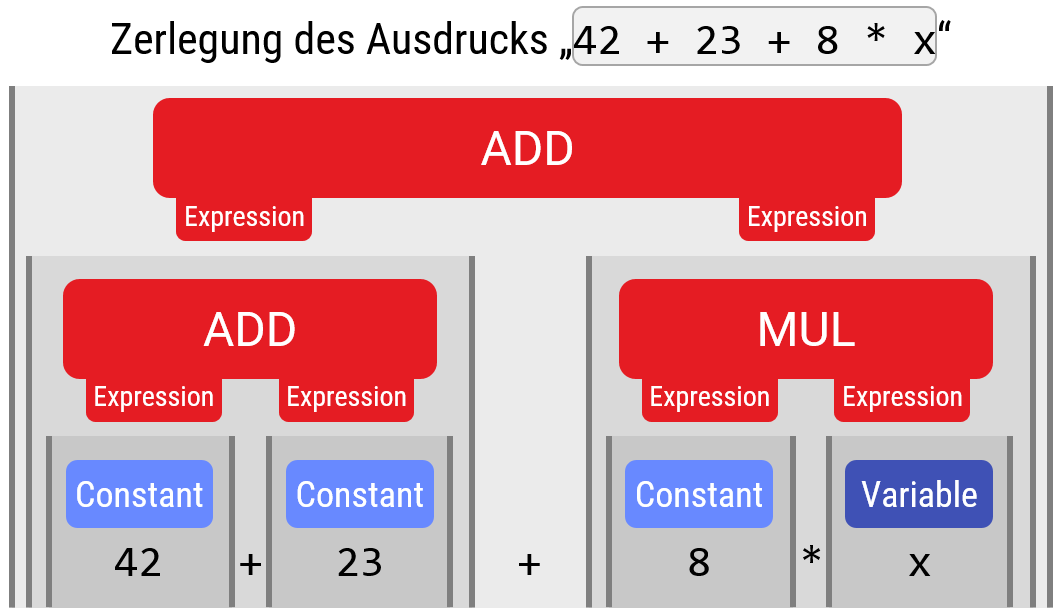
Abbildung 2: Zerlegung des arithmetischen Ausdrucks \(42+23+8*x\) in Bausteine, die einen Operandenbaum bilden. In dieser Grammatik ist es schwieriger zu erkennen, wo die Grenzen der Bausteine liegen (beim Baustein Addition ist es sogar immer mehrdeutig; die Präzedenz Addition/Multiplikation kann man in der Grammatik einbauen; s.u.).


Leider ist dieses Problem nicht immer einfach. Für unsere Beispielgrammatik gibt es z.B. keine eindeutige Lösung (und das ist ein Problem; die Bedeutung wäre damit nicht mehr klar definiert):


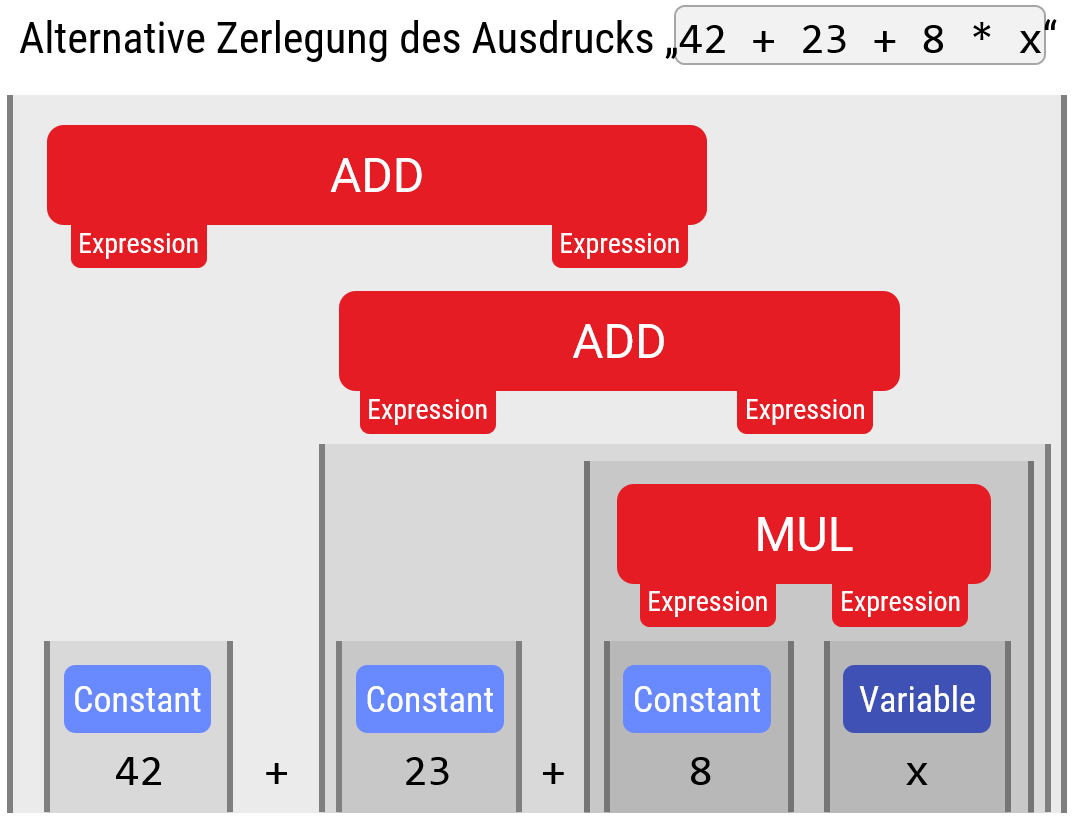
Abbildung 3: Hier sieht man das Problem: Da keine expliziten Klammern gesetzt wurden, könnten man die beiden Additionsoperationen auch assoziativ vertauschen (was natürlich mathematisch keinen Unterschied macht, und numerisch, bei Fließkommazahlen, nur einen sehr geringfügigen).)


Für das Beispiel mit arithmetischen Ausdrücken, wie hier gezeigt, kann man die Mehrdeutigkeit zwischen Multiplikation und Addition klären, indem man die Regeln geschickter schachtelt. Das Bild unten zeigt die Standardlösung für dieses Problem:


Abbildung 4: Das Problem, dass Punktrechnung eine höhere Priorität haben soll, läßt sich durch eine Änderung der Grammatik abbilden (der Baustein MExpr ist spezieller und klammert daher enger). Das Problem der Mehrdeutigkeit beim Plus lässt sich so nicht beheben — hier braucht man eine (nicht-kontextfreie) Sonderregel im Parser.


Die gerade beobachte Mehrdeutigkeit bei der Addition löst dies aber nicht; hier muß man im Parser zusätzlich festlegen, daß die Ausdrücke nach links oder rechts geklammert werden sollen (Links-/Rechtsassoziativität'').


Man kann es sich natürlich auch einfach machen, und eine Sprache so definieren, dass es sehr einfach wird, die Grenzen der Bausteine und deren Schachtelung zu erkennen. Dazu ist hinreichend, wenn man Anfang und Ende von Blöcken eindeutig markiert, und auch den Typ des Bausteins explizit kennzeichnet. Ein Beispiel für eine solche Sprache ist LISP, in der der Operatorbaum als Klammergebirge kodiert wird, und die Operation immer am Anfang direkt benannt wird:


Abbildung 5: Die Sprache Lisp vermeidet alle Mehrdeutigkeiten, indem ein vollgeklammterter Ausdruck verwendet wird, bei dem der Name des Operators immer direkt am Anfang jeder Klammer steht, gefolgt von zwei Platzhaltern für Operanden. Ein Parser hierfür ist extrem einfach zu programmieren. Dafür sieht der Code dann etwas unintuitiv aus.


Abbildung 5: Hier ein Beispiel dafür, wie unser Beispielausdruck in LISP geschrieben würde. Einfach zu parsen — ja, aber nicht unbedingt ästhetisch überzeugend.


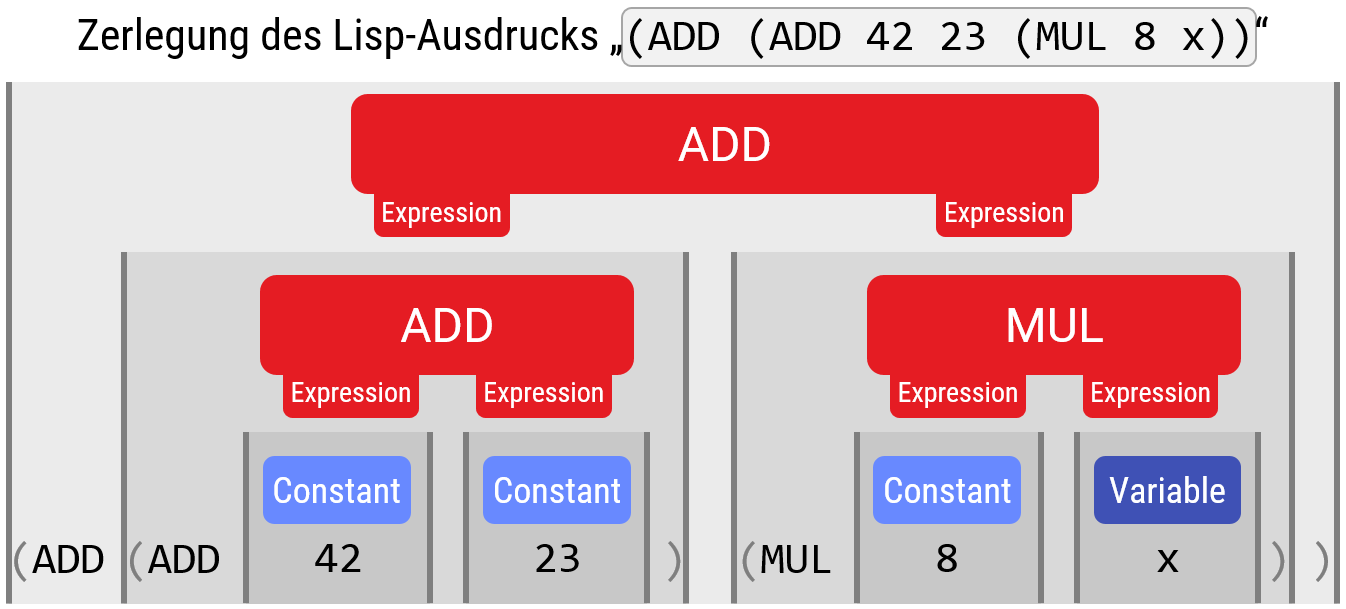
Es gibt viele Sprachen, die speziell dafür entworfen wurden, um möglichst einfach zurück in Bäume verwandelt werden zu können. Dazu zählen z.B. XML oder JSON, sowie die meisten Binärformate (auch dies sind oft kontextfreie Schachtelungen von Datenpaketen) von verschiedenen Anwendungsprogrammen, wie z.B. PDF.


Wie funktioniert nun ein Parser?
Die Theorie der kontextfreien formalen Sprachen wird also durch zwei Probleme kompliziert: Zum einen kann es unauflösliche Mehrdeutigkeiten geben, und wir müssen dafür sorgen, dass dies in unserer Codierung keinen Probleme macht. Leider ist dies nicht so einfach zu garantieren. Zum zweiten ist es nicht immer ganz einfach, zu erkennen, wo die Grenzen der Bausteine liegen, auch wenn dies durch die Grammatik eindeutig festgelegt ist. Der einfachste Ansatz wäre ein Backtrackingalgorithmus, der alle Kombinationen, den String in Bausteine aufzuteilen, einfach brute-force durchprobiert, aber das wäre exponentiell (also: viel zu) teuer.


Es gibt Parsingalgorithmen, die jede kontextfreie Sprache (in geeignet transformierter Form der Grammatik) in \(\mathcal{O}(n^3)\) Zeit in einen Baum übersetzt (für \(n\) Eingabezeichen). Das ist zwar nicht unmöglich teuer, aber immer noch sehr praxisfern. In der Praxis nutzt man daher in der Regel spezielle Typen von Grammatiken (LR(0), LR(1), LR(k), LL(k) u.ä.), die den Entwurf der Sprache zu Gunsten der Effizienz etwas einschränken. Dazu gehören dann effiziente Parsingalgorithmen wie der LR-Parser (Bottom-Up-Parser) oder Recursive Descent Parser (Top-Down-Parser). Diese Grammatiken zeichenen sich dadurch aus, dass man nur einige wenige (maximal k) aufeinanderfolgende Symbole anschauen muß, um mit Sicherheit entscheiden zu können, wie der Baum aufgabaut werden muß (eine volle Klammerung wäre z.B. eine LR(0)-Sprache — bei jeder Klammer weiß man sofort, was zu tun ist).


In unserer Aufgabe schauen wir uns eine einfache Sprache für mathematische Ausdrücke an, für die man einen einfachen Parser direkt per Hand bauen kann. Der korrespondierende Algorithmus, den wir hier vorschlagen, ist übrigens ein Spezialfall eines shift-reduce parsers für (im allgemeinen) LR(k)-Grammatiken.


Dieser Parser baut immer Teilbäume von links nach rechts auf. Hierzu sollten wir uns nochmal genau Abbildung 2 anschauen: geht man von links nach rechts durch die Zeichenkette, erkennt man nacheinander die Teilbäume (42), dann ((42)+?), dann ((42)+(23)), dann (((42)+23) + ?), und so weiter. Wenn man den Baum so aufbaut, muß man zwei Entscheidungen treffen:

  1. Wo ist die Grenze eines Elementes, und
  2. Wie wird der Baum geordnet (hier gibt es zwei Möglichkeiten: Soll der Operator linker Teilbaum und der aktuelle Operator der neue Wurzelknoten werden, oder umgekehrt?).

Um diese Frage zu beantworten, schaut der Parser immer einen Operator in die Zukunft, und legt noch ungeordnete Teillösungen auf einem Stack ab, um diese später zusammenzusetzen. Die Ordnung wird dabei entweder durch die Grammatikregeln (Schachtelungsordnung) entscheiden oder es wird eine zusätzliche Assoziativitätsregel verwendet (wenn man den Parser von Hand schreibt, wie auf diesem Aufgabenblatt, spielt diese Unterscheidung keine Rolle; wichtig wäre das nur, wenn man einen Parsergenerator schreiben wollte, der aus Grammatiken automatisch einen Parser konstruiert).


Im Prinzip kann man mit diesem Formalismus automatische Übersetzer für beliebige Programmiersprachen schreiben (Parsergeneratoren wie z.B. Lex & Yacc); für unser Aufgabenblatt geht das natürlich zu weit; die handgeschriebene Lösung ist einfach und braucht im Vergleich deutlich weniger Zeilen Code.