



Institut für Informatik
Thomas Kemmer
Wintersemester 2025/26Mathematische Modellierung am Rechner II
Übungsblatt 6: Abschlussprojekt
Letzte Änderung : 06 October 2025, 14:23 UhrAbnahmetermin : 02. Februar 2026 (Abgabe bis 10:00 Uhr)
Wichtige Information
Liebe Studierende,
auf diesem Blatt haben Sie die Wahl zwischen drei Projekten. Nur eines muss implementiert und vorgestellt werden. Lesen Sie den Abschnitt Über das Übungsblatt und entscheiden Sie sich zuerst für eine der beiden Spezialisierungen oder für die letzte Aufgabe. Aufgabe 0 beinhaltet die gemeinsamen Grundfunktionen, die Sie für die ersten beiden Aufgaben benötigen. Während Aufgaben 1 und 2 wieder Probleme aus Grafik/Geometrie und Physik betreffen, (wir wie sie in diesem und auch dem letzten Semester bearbeitet haben), behandelt Aufgabe 3 ein algorithmisches Problem aus der kombinatorischen Optimierung ähnlich zu Blatt 1 dieses Semesters.
Wie beim Abschlussprojekt des letzten Semesters handelt es sich auch hier um eine kreative Aufgabe, wobei das gelernte der Veranstaltung angewendet werden kann. Dieses Blatt vermittelt also keine grundsätzlich neue Theorie.
Viel Spaß bei der Bearbeitung wünscht Ihnen das "Praktische Modellierung am Rechner"-Team.
Das Basisprogramm für Aufgaben 1 und 2:
Als erstes schauen wir eine spezielle Art von Spline-Kurven an (siehe Aufgabe 1, Blatt 04), die in vielen Anwendungen ihre Verwendung findet; die Bézier-Kurven. Wir implementieren als erstes eine einfache Anwendung, mit der wir komfortabel zusammengesetzte Bézier-Kurven (a.k.a. Pfade) zeichnen können.Dies können wir nun verwenden, um etwas interessantere Themen zu behandeln. Wählen Sie dazu eine der beiden folgenden Spezialisierung dieses Grundkonzeptes:
Ihr eigener Vektorgraphik-Editor:
Erstellen Sie ein Programm,- das eine Hand voll Tools bereithält, um Vektorgraphiken bequem erstellen und bearbeiten zu können. Darin eingeschlossen ist die Verarbeitung von Text, Stil (Farbe, Farbverläufen, Schatten, Transparenz und Rändern) und einfache Transformationen auf den Grundobjekten.
- mit dem Sie die erstellten Vektorgraphiken speichern können. (Um sie dann in einem anderen Programm wie etwa Firefox oder Power Point weiterverwenden zu können).
- kontrollpunktgesteuerte Transformation
- die automatisierte Vereinfachung „komplizierter“ Pfade
Eine Implementierung des Spiels Line Rider :
Das ist Line Rider. (Spielen Sie hier die Online-Version).Erstellen Sie ein Programm mit dem Sie,
- Level erstellen, speichern und laden können
- die Simulation starten, pausieren, vor- und zurückspulen können (um einfach noch raffiniertere Stunts zu erstellen)
- die Kollisionserkennung eines Objektes mit einer Kurve
- wie man Drehimpulserhaltung (approximativ oder exakt) implementiert (die Line Rider-Figur dreht sich je nach Rampe und Geschwindigkeit in der Luft).
Aufgabe 0: Grundfunktionen & Bézier-Kurven-Editor
Bewertung: 35 Punkte
Als erstes Implementieren wir ein Basisprogramm, von dem aus die unten aufgeführten Spezialisierungen abgeleitet werden können.
Auf dem letzten Blatt haben wir bereits mit Funktionsräumen gearbeitet. Dabei hatten wir eine Funktionenbasis gewählt und mithilfe von Kontrollpunkten eine zweidimensionale parametrische Kurve erstellt.
Hier schauen wir uns Bézier-Kurven an. Bézier-Kurven entstehen durch eine besondere Funktionsbasis, nämlich \[ \left\{\frac{n!}{i!(n-i)!} t^i(1-t)^{n-i} \mid| n,i \in \mathbb{N}\right\}. \] Die Theorie und ihre Eigenschaften werden für gewöhnlich in Computergraphik-Vorlesungen behandelt, soviel aber bereits jetzt:
- sie können sehr effizient berechnet werden
- die Kurve geht stets durch den ersten (und letzten) Kontrollpunkt
- die Kurve geht von dort aus in Richtung des nächsten (bzw. vorletzten) Punktes (d.h. die Kurve ist leicht Kontrollierbar)
- Nachteil gegenüber Splines ist, dass die Änderung eines Kontrollpunktes stets die globale Kurve ändert. Dies war auf dem letzten Blatt nicht so.
Wir werden hier jedoch nur einen Spezialfall dieses Funktionenraumes verwenden, die kubischen Bézierkurven: Für vier Punkte \(K_1,K_2,K_3,K_4 \in \mathbb{R}^n\) lautet die parametrische Form der kubischen Bézier-Kurve \[ f(t) := (1-t)^3K_1 + 3(1-t)^2 t K_2 + 3(1-t) t^2 K_3 + t^3 K_4,\qquad t \in [0,1]. \] Beachten Sie, dass dies eine Verallgemeinerung der linearen Interpolation \((1-t)K_1 + tK_2,\, t\in [0,1]\) ist. (Weiteres zur Theorie dieser Funktionen können Sie in der Computergraphik-Vorlesung lernen).
Ziel dieser Aufgabe ist es, einen einfachen interaktiven Editor für kubische Bézier-Kurven zu erstellen.




Die Bounding Box-Transformation, die am Ende der Animation verwendet wird, um Größe und Ausrichtung des „i“ anzupassen wird in der Spezialisierung 1 (Vektorgraphik-Editor) besprochen.
Aufgaben
- Lesen Sie als erstes das Kapitel Hintergrundwissen zum Thema Bézier-Kurven durch.
- Implementieren Sie als erstes eine Anwendung, in der Sie wie abgebildet beliebig viele Kontrollpunkte \(K_1,\dots, K_n\) setzen, verschieben und wieder löschen können. Wie sie das Manipulieren und Setzen der Punkte realisieren (z.B. Doppelklick für Setzen/Löschen, Drag'n'Drop für Verschieben) sei ganz Ihnen überlassen.
- Implementieren Sie nun das Zeichnen der Bézier-Kurven. Fassen Sie dazu je die vier aufeinander folgende Punkte \(K_{3i},K_{3i+1},K_{3i+2},K_{3i+3}\) zu einem Kurvensegment zusammen. Ein Pfad entsteht dadurch, dass (wie in den Indices angedeutet) der jeweils letzte Kontrollpunkt eines Segmentes bereits der erste Kontrollpunkt des nächsten Segmentes ist.
Um die Kurve tatsächlich zu zeichnen reicht es aus, jedes Kurvensegment mit \(m\) Punkten abzutasten und die resultierenden Liniensegmente einzuzeichnen.
Typischerweise zeichnet man nur die Verbindungen der Kontrollpunkte \(K_{3i}\) und \(K_{3i+1}\), sowie \(K_{3i+2}\) und \(K_{3i+3}\) und erhält so die Kontrolle über den Austrittswinkel aus Punkt \(K_{3i}\) bzw. den Eintrittswinkel in Punkt \(K_{3i+3}\). - Fügen Sie die Möglichkeit ein in der Ebene zu navigieren und zu zoomen. Hinweis: Nach der Viewport-Transformation (Verschiebung der Ebene oder Zoom) müssen Sie beim Abfragen der Mausposition (z.B. beim Drag'n'Drop) darauf Achten, dass die Position der Maus mittransformiert wird.
- Realisieren Sie auch die Möglichkeit mehrere separate (unverbundene) Pfad-Objekte zu erstellen und diese jeweils als ganzes mausgesteuert verschieben zu können
Hinweis:- Im Beispielvideo wurde dies so gelöst, das ein Rechtsklick die Auswahl aufhebt und ein Linksklick die nächstgelegene Kurve zur Maus auswählt (sofern keine in der Nähe ist, wird eine neue erstellt). Jeder weitere Linksklick fügt einen neuen Punkt ans Ende der aktuellen Kurve an.
- Als Idee können sie das Verschieben des ganzen Pfades durch einfaches Ziehen an der Bounding Box realisieren.
- die Transformation (Rotation und Skalierung) am Ende der Animation muss an dieser Stelle nicht implementiert werden. Dies ist Gegenstand aus Spezialisierung 1.
Spezialisierung 1: Vektorgraphik-Editor
Bewertung: 65 Punkte
Vektorgraphiken ist ein unerlässliches digitales Werkzeug, das in von Design über technisches Zeichnen (CAD) bis zum Rendern einer Internetseite seine Anwendung findet. Wir möchten in dieser Aufgabe einen eigenen Vektorgraphik-Editor implementieren.
Ziel ist es Vektorgraphiken erstellen, bearbeiten und so speichern zu können, dass wir sie in einem anderen Programm weiterverarbeiten können.
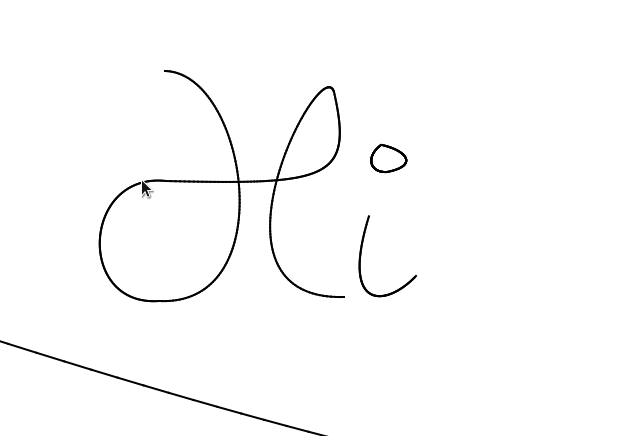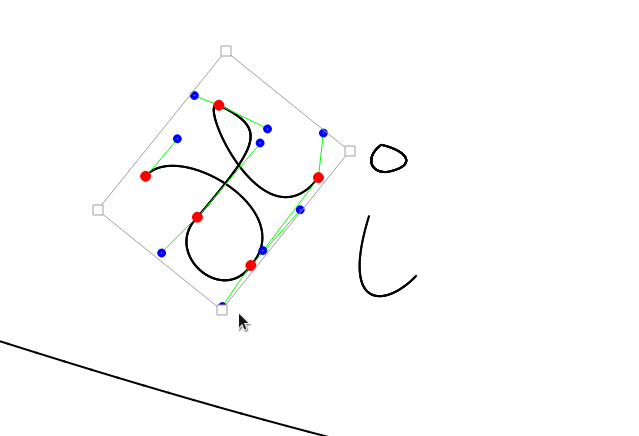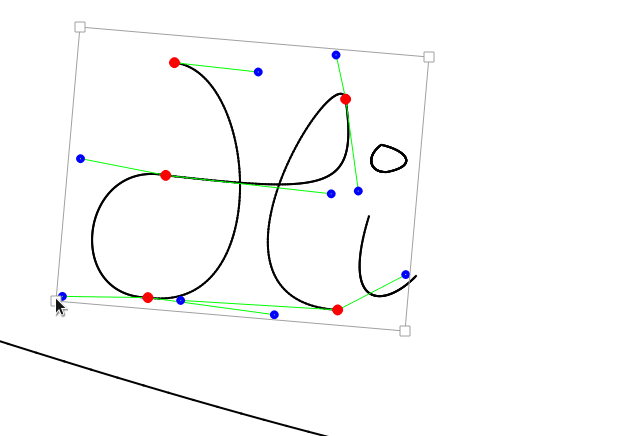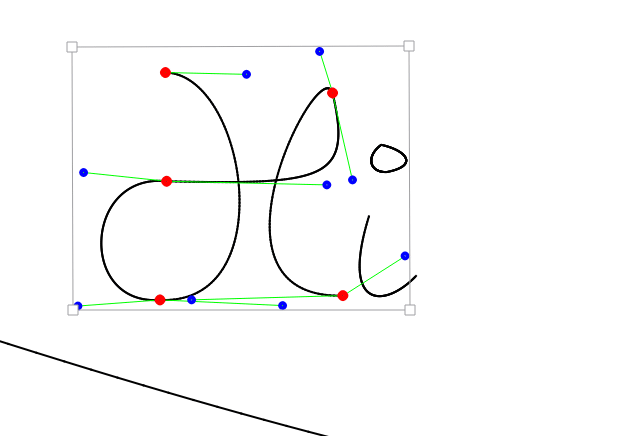
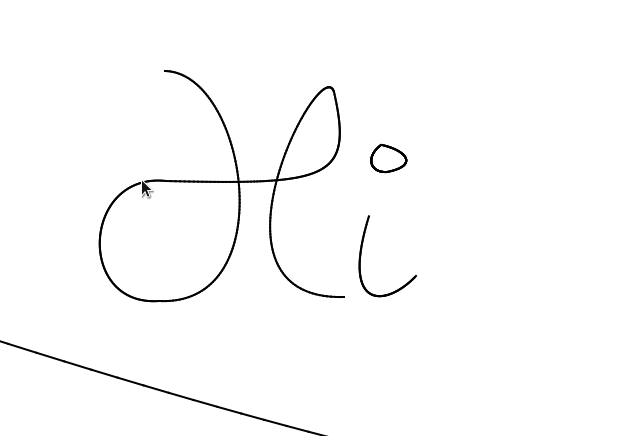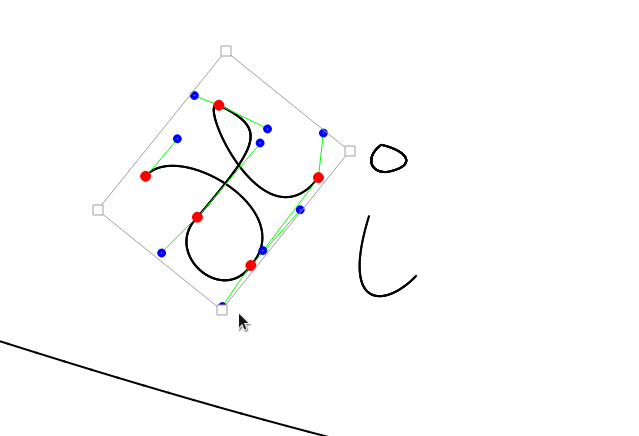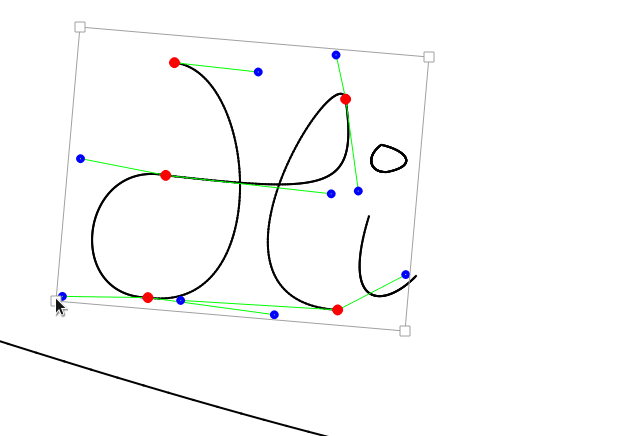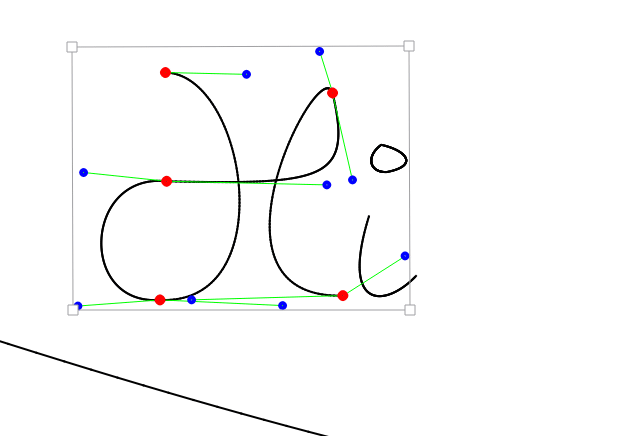
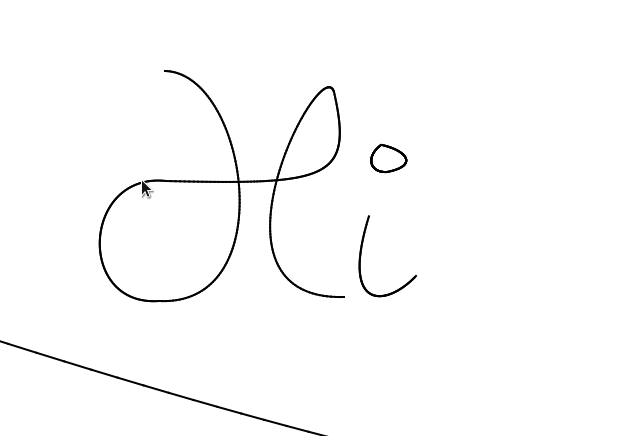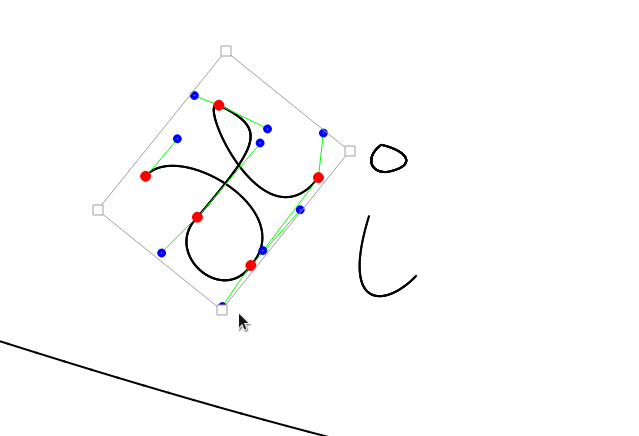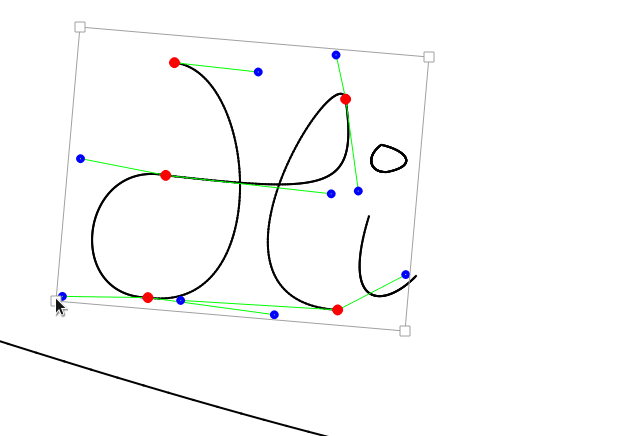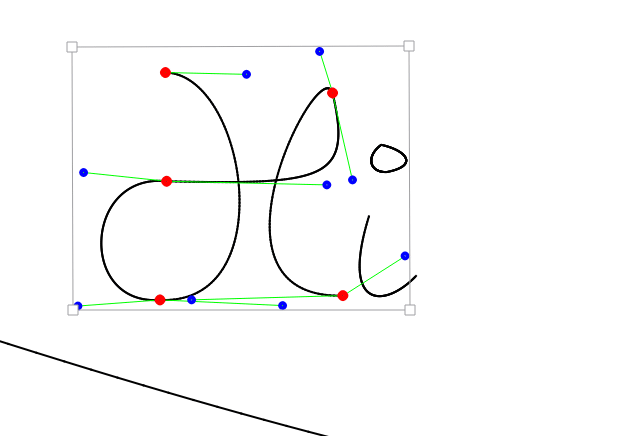
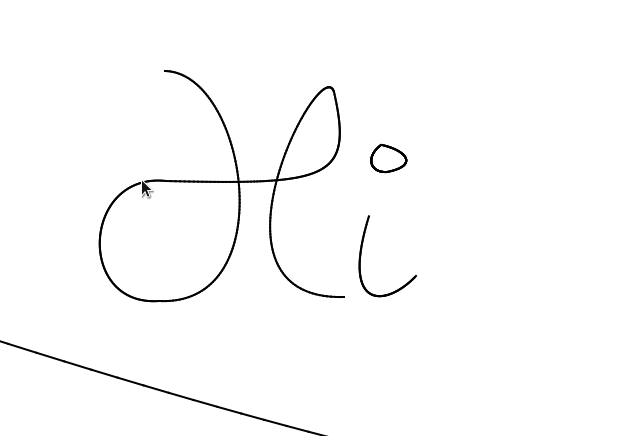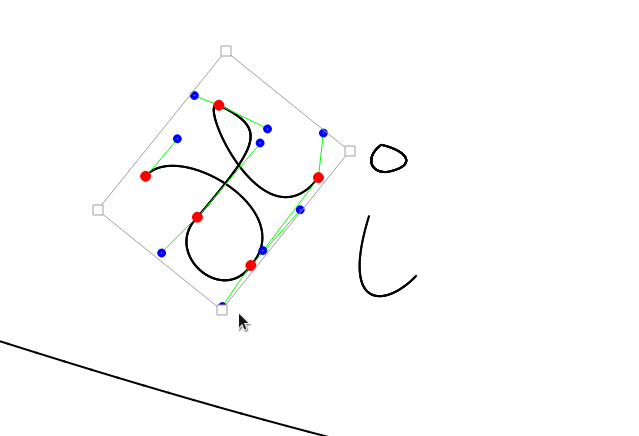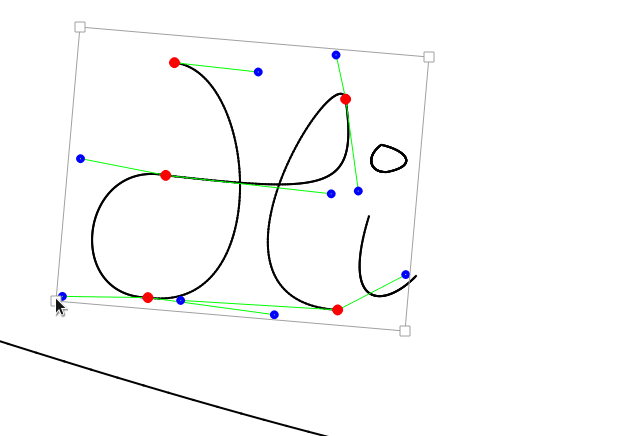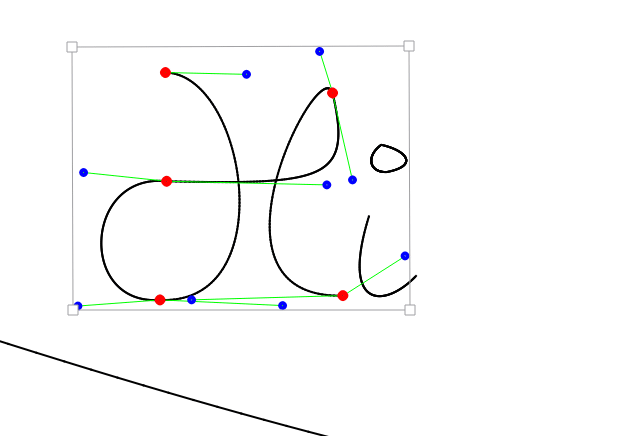
Aufgaben
- Erweitern Sie das Basisprogramm so, dass zusätzlich zu den Bézier-Kurven auch die Funktionalitäten bereitstellt verschiedene primitive Objekte (verschiedene Formen, Farbverläufe und Schrift) in einer Szene zu erstellen, verschieben und zu löschen.
Hinweise:- Funktionalitäten wie etwa das Navigieren sollten dabei erhalten bleiben
- Bestimmen und Zeichnen Sie algorithmisch das kleinste, umschließende, achsenorientierte Rechteck eines jeden Objektes.
Hinweis:- Sie benötigen dazu lediglich den Minimal bzw. Maximalwert von \(x\)- und \(y\)-Achse.
- Einfaches Verschieben ist häufig nicht genug. Überlegen Sie sich, wie sie interaktive Drehungen und Skalierungen (beispielsweise mit den Eckpunkten der Bounding Box) realisieren können.
Hinweis:- bestimmen Sie die Winkeländerung bzw. Abstandsänderung vom Kontrollpunkt, bevor eine Transformation durchgeführt wurde (dies ist wichtig, damit die Drehskalierung numerisch stabiler ist) zum Zentrum des Objektes.
- Der Winkel zwischen zwei Vektoren \(a\) und \(b\) kann auf mannigfaltige Arten und Weisen bestimmt werden. Viele geben jedoch nur den eingeschlossenen Winkel \([0,\pi]\) an. In 2D können Sie mit folgender Methode den Winkel \(\in [0,2\pi]\) im Uhrzeigersinn bestimmen.
def angle(a,b): ang1 = np.arctan2(*a) ang2 = np.arctan2(*b) return (ang2-ang1) % (2*np.pi)
- Fügen Sie nun Farben (inklusive Transparenz) und Stile für Kontur und ausgefüllte Flächen ein.
Hinweise:- In Qt sind all diese Funktionen bereits vorimplementiert. Überlegen Sie sich, wie sie diese Funktionen bequem und kreativ verwenden können.
- Siehe QPainter-Dokumentation oder QLinearGradient-Dokumentation
QPainter.setBrush(füllt die Fläche)QPainter.setPen(malen des Randes)QLinearGradient(Farbverlauf, kann mit setBrush anQPainterübergeben werden)
- Realisieren Sie den zuschaltbaren Stil „weicher Schatten“.
Dazu zeichnen wir das betreffende Objekt mehrmals (\(\sim 100 \times\)) und immer wieder leicht verschoben unter das Originalobjekt. Genauer verschieben wir es um Punkt \((x,y)\) um mehrere Pixel mit einer Normalverteilung (die Standardabweichung reguliert die Streuung) und einem geringen, aber festen Alpha-Wert (\(\approx 1\%\)). - Exportieren Sie die Graphik als SVG. Glücklicherweise liefert Qt bereits die Möglichkeit mit das gezeichnete Bild als SVG zu exportieren. QSvgGenerator tritt dabei an die Stelle des Bildes/des Widgets und kann auf herkömmliche Weise mit einem QPainter bemalt werden. Sie müssen also ihre Mal-Methode lediglich mit dem QSvgGenerator statt des Widgets aufrufen.
Die gespeicherte SVG-Datei können sie nun mit einem anderen Vektorgraphik-Editor wie Inkscape oder auch Ihrem Browser öffnen.
Spezialisierung 2: Line Rider
Bewertung: 65 Punkte
In dieser Aufgabe werden wir die Technik an unser Basisprogramm anpassen und wieder etwas Physik einführen. Als Ziel soll die Sandbox-Simulation Line Rider implementiert werden.
Line Rider ist ein Computerspiel, das ein slowenischer Student 2006 erfand und seither tausendfach aufgegriffen wurde. Beispielvideo (mit Musik). (Spielen Sie hier selbst die Online-Version). Um das Problem so schön zu lösen, wie die Implementierung auf der Internetseite bzw. im Video bedarf eines komplexeren physikalischen Modells, wie etwa Position Based Dynamics oder ähnliches. Dort wird jedes Objekt als eine Punktwolke angesehen, dessen Elemente bestimmte Bedingungen untereinander erfüllen müssen. Beispielsweise sollen hier die Eckpunkte des Schlittens stets zusammenhängen und auf Kollisionen mit den Linien reagieren. Eine andere Punktwolke (die des Spielers) ist durch Federn an den Schlitten gebunden, die jedoch bei zu großer Kraftausübung reißen können.
Da diese Systeme Gegenstand von Computergraphik-Vorlesungen sind, werden wir hier eine viel einfachere Methode implementieren. Dies ist jedoch nur ein Vorschlag; gerne können Sie sich überlegen, wie Sie Ihre Simulation gestalten möchten.




Aufgaben
- Erweitern Sie das Basisprogramm so, dass Sie diese vier Arten von Bezier-Pfaden Zeichnen können:
- Blau, Eis bzw. Schneebahn (keine Reibung)
- Grau, Schotter (wird den Schlitten bremsen)
- Grün, wird bei der Kollisionserkennung ignoriert
- Orange, Speedup!
- Fügen Sie das Speichern bzw. Laden von Strecken ein.
- Zeichnen Sie Ihre Spielfigur (mindestens jedoch einen Schlitten)
Hinweis: Wichtig zu beachten ist, dass sie die Figur stets in lokalen Koordinaten zeichnen müssen, da sich der Schlitten abhängig von der Steigung der Strecke auch drehen lassen muss. - Nun zur Simulation. Starten Sie damit eine
update()Funktion zu implementieren, die automatisch durch einenQTimeraufgerufen wird.
Stellen Sie sich nun vor, die Line Rider-Figur ist zu Beginn nur eine Kugel. Implementieren Sie als erstes den freien Fall der Spielfigur / der Kugel. Zur Erinnerung: \[ x \leftarrow v\cdot t_\text{Schritt},\, v \leftarrow a \cdot t_\text{Schritt},\, a = \text{const}. \] - Der wichtigste, jedoch auch schwierigste Punkt ist nun die Kollision mit der Strecke. Am einfachsten ist es, die Kollision nicht mit der Bezier-Kurve, sondern mit der Abtastung, also den Liniensegmenten durchführen, die bereits für das Zeichnen der Kurve berechnet wurden.
Hierzu gibt es zum Beispiel diese zwei einfache Lösungen:- Nutzen Sie einen Algorithmus, der Prüft, ob eine Kugel ein Liniensegment schneidet.
- Nutzen Sie einen Algorithmus, der Prüft, ob zwei Liniensegmente sich schneiden. In dem Fall können Sie das Liniensegment finden, durch das das Zentrum der Kugel im nächsten Simulationsschritt durchkreuzt wird.
Sofern Sie nun das Liniensegment gefunden haben, können Sie sich nun überlegen, wie die Geschwindigkeit abgelenkt werden muss, damit ein realistisches Verhalten der Kugel entsteht.
Hinweis:- Sorgen Sie dafür, dass bei einer Kollision, der Schlitten etwas nach oben gesetzt wird, oder die Geschwindigkeit etwas nach oben zeigt, sonst fällt die Figur im nächsten Schritt durch die Ebene.
- die Normale eines Liniensegmentes in 2D lässt sich einfach bestimmen: Die Normale zu \((x,y)\) lautet \((-y,x)\).
- die Projektion eines normierten Vektors (Länge beträgt 1) auf einen anderen normierten Vektor lautet: \( (a \cdot b) \cdot b\), wobei der erste Term ein Skalarprodukt enthält, also eine Zahl ist, die gesamte Formel jedoch einen Vektor ausgibt.
- Falls die Kugel sich nun richtig durch die Spielwelt bewegt, können wir nun die Spielfigur so drehen, dass der Schlitten stets zum Boden ausgerichtet ist.
Hinweis:- bestimmen Sie den Winkel zwischen Ursprungsschlitten und kollidiertes Liniensegment
- Der Winkel zwischen zwei Vektoren \(a\) und \(b\) kann auf mannigfaltige Arten und Weisen bestimmt werden. Viele geben jedoch nur den eingeschlossenen Winkel \([0,\pi]\) an. In 2D können Sie mit folgender Methode den Winkel \(\in [0,2\pi]\) im Uhrzeigersinn bestimmen.
def angle(a,b): ang1 = np.arctan2(*a) ang2 = np.arctan2(*b) return (ang2-ang1) % (2*np.pi)
- Wir können die Simulation nun starten. Um jedoch interessante Stunts zu erstellen, benötigen wir noch die Möglichkeit des Pausierens und des Vor- und Zurückspulens. Implementieren Sie dies.
- Überlegen Sie sich zuletzt wie Sie einen flatternden Schal im Wind implementieren können und realisieren Sie dies.
Aufgabe 3: Paralleles Sokoban
Bewertung: 100 Punkte
Wählen Sie dieses Abschlussprojekt müssen Sie selbstverständlich die Grundfunktionen aus Aufgabe 0 nicht bearbeiten.
Das Spiel Sokoban ist sicherlich jedem bekannt: Auf einem gitterförmigen Spielfeld sollen Kisten auf bestimmte Zielfelder geschoben werden. Dabei kann sich die Spielfigur immer nur ein Feld waagerecht oder senkrecht bewegen und dabei maximal eine Kiste vor sich herschieben. Das ist nur dann möglich, wenn das Feld hinter der Kiste frei ist (also nicht durch eine andere Kiste oder Wand blockiert wird). Ziel ist es, dabei insgesamt so wenig wie möglich Schritte zu benötigen.
Diese klassische Variante ist natürlich völlig langweilig. Kisten nacheinander, also sequentiell, zu schieben, ist heutzutage natürlich nicht mehr zeitgemäß. Wir wollen das ganze parallelisieren: statt auf einem Feld spielen wir gleich auf vier Feldern, dabei aber nur mit einer jeweils einer einzigen Kiste. Wenn wir eine Figur bewegen, dann bewegen sich alle Figuren in jedem der Felder in eben diese Richtung. Drückt man also die "Nach-Oben-Taste", dann bewegen sich alle Spielfiguren ein Feld nach oben. Ist das einer Figur nicht möglich (z.B. weil in dem entsprechenden Feld eine Wand ist), dann bleibt diese Figur stehen (die Figuren in den anderen Feldern bewegen sich aber trotzdem). Ziel ist es, jede Kiste in jedem der vier Felder ins Ziel zu schieben, und das mit so wenigen Zügen (also Tastendrücken) wie möglich. Die unten stehenden Bilder zeigen die jeweiligen Startpositionen. Die gelben Quadrate sind die Kisten, der grüne Kreis die Spielfigur. Ziel ist es, die Kiste zum jeweiligen Ausgang zu schieben.
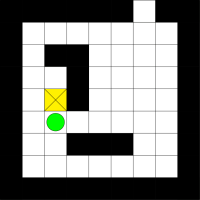



Feld 1
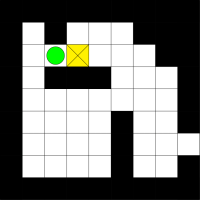



Feld 2
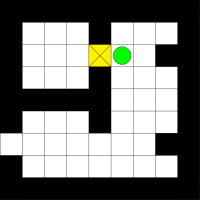



Feld 1
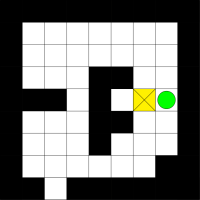



Feld 2
Aufgaben
- Entwickeln Sie ein Programm, das die vier Spielfelder darstellt, so dass man mit den vier Pfeiltasten das Spiel spielen kann.
- Eine gute Lösung zu finden ist nicht leicht. Entwickeln Sie einen Algorithmus, der automatisch eine Lösung bestimmt. (siehe auch die Hinweise am Ende dieser Aufgabe) Beginnen Sie damit, zunächst eine Lösung in nur einem Feld zu bestimmen (die anderen drei Felder werden ignoriert).
- Erweitern Sie Ihr Programm nun so, dass Sie zwei Felder gleichzeitig betrachten können.
Tipp: Wenn Sie Aufgabe 2 gelöst haben, können Sie auch leicht eine Lösung für Aufgabe 3 finden (wie?), auch wenn diese Lösung dann nicht notwendig bestmöglich ist (warum?). - Schaffen Sie es auch, eine Lösung für drei oder sogar alle vier Felder zu finden? Was ist die beste Lösung (d.h. die kleinste Anzahl an Zügen), die Sie finden können? Ist diese (beweisbar) optimal?
Hinweise:
- Die größte Hürde dieser Aufgabe ist zunächst, eine Datenstruktur zu entwickeln, mit welcher die Spielsituation und Züge dargestellt werden können. Schauen Sie dazu noch einmal auf Blatt 1, das enthält sehr wertvolle Tipps!
Die einfachste Möglichkeit ist es, das Spiel als Graph \(G=(V,E)\) darzustellen: die Knoten bilden die Zustände des Spiels, die Kanten entsprechen den vier möglichen Zügen. Für das Spiel in einem einzelnen Feld wäre z.B. \[ V := \{(x_f,y_f,x_k,y_k) \in \{1, \ldots, 9\}\} \] die Menge der möglichen Zustände, wobei \((x_f,y_f)\) die Position der Figur und \((x_k,y_k)\) die Position der Kiste ist. Ein Zug nach rechts entspricht dann einer Kante \(((x_f,y_f,x_k,y_k),(x_f+1,y_f,x_k,y_k))\) falls \((x_k,y_k) \ne (x_f+1,y_k)\) ist (d.h. falls die Kiste nicht rechts neben der Figur steht) und \(((x_f,y_f,x_k,y_k),(x_f+1,y_f,x_k+1,y_k))\) falls die Kiste genau rechts neben der Figur steht (also mit verschoben wird). Beachten Sie, dass nicht alle Zustände/Knoten tatsächlich erlaubt sind (z.B. darf die Figur nicht in einer Wand stehen). Ein Lösung entspricht dann einem Weg in diesem Graphen vom Startzustand zu einem Zielzustand, wobei der Zielzustand der ist, bei dem die Kiste auf dem Zielfeld steht. - Versuchen Sie nun, eine bestmögliche Lösung für das 1-Feld-Problem zu finden. Dazu müssen sie einen kürzesten Weg in diesem Zustandsgraphen finden.
- Überlegen Sie, wie der Zustandsgraph für das 2-Felder-Problem aussieht. Können Sie ihren Algorithmus entsprechend anpassen?
- Für drei oder mehr Felder wird der Zustandsgraph riesig. Dieser kann dann nicht mehr explizit gespeichert werden (außer Sie haben sehr viel Speicher). Aber glücklicherweise müssen wir ihn auch nicht explizit speichern. Der Algorithmus, den Sie auf Blatt 1 kennengelernt haben, muss nur für jeden Knoten die möglichen Nachbarknoten (aber nicht alle Knoten) kennen. Das hatten wir auch im verbesserten Algorithmus ausgenutzt, der nicht mehr alle Knoten besuchen muss. Damit der Algorithmus aber schnell wird, benötigen wir wie auf Blatt 1 untere Schranken. Der Zustandsgraph entspricht aber keinem Straßennetz, wir können also keine geometrische Information wie euklidische Distanzen (Luftlinie) verwenden wie auf Blatt 1. Wenn wir aber bereits die Optimallösung für ein oder zwei Felder kennen, wie können wir dann untere Schranken (also eine mindestens benötigte Anzahl von Zügen) für das 3 Felder Problem bestimmen?