JGU Logo JGU Logo JGU Logo JGU Logo

Institut für Informatik

Markus Blumenstock
Wintersemester 2024/25

Mathematische Modellierung am Rechner II

Übungsblatt 4: Funktionenräume
Letzte Änderung : 09:41 Uhr, 01 November 2020
Abnahmetermin : 19. Dezember 2023

I don't do Fourier jokes with enough frequency.
Quelle mit Fourier-Comic


Über dieses Übungsblatt
Auf diesem Aufgabenblatt schauen wir uns an, wofür man abstrakte (axiomatisch definierte) Vektorräume praktisch einsetzen kann.
Das wahrscheinlich wichtigste Anwendungsgebiet sind lineare Räume von Funktionen, also Strukturen, in denen Funktionen als Punkte in einem (sehr hoch-dimensionalen) Raum aufgefasst werden.
Mit diesen Funktionen kann man dann wie mit Punkten rechnen. Zum Beispiel kann man sie addieren oder mit einer Zahl multiplizieren, man kann „hübsche“ Exemplare aus dem Funktionenraum als Linearkombinationen von Basisfunktionen zusammenstellen (Aufgabe 1). Wir können aber auch eine geschickte Basis für den ganzen Funktionenraum aussuchen; damit sieht man bestimmte Eigenschaften viel eher als in einer Standardbasis oder kann diese zur Kompression verwenden (Aufgabe 2 und Aufgabe 3). Für jeden dieser Fälle schauen wir uns ein einfaches Beispiel an.
Aufgabe 1 und 2 betrachten wir parametrische 2D-Kurven, also Funktionen, die einen reellen Parameter auf 2D Punkte abbilden (siehe Abschnitt Hintergründe am Ende dieses Dokuments für eine Erläuterung der benutzten Konzepte).
Aufgabe 3 verwendet reellwertige Funktionen in zwei Variablen — dies beschreibt ein schwarz-weiß Foto, d.h. jedem Gitterpunkt wird ein Funktionswert (der Grauwert) zugewiesen.

Aufgabe 1: Spline Kurven

Bewertung: 40 Punkte


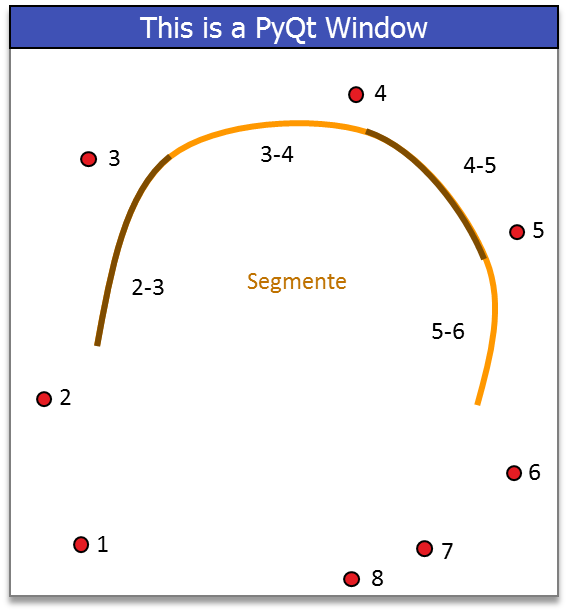
Splines mit PyQt Splines mit PyQt Splines mit PyQt Splines mit PyQt
Die Lösung könnte ungefähr so aussehen (dies ist nur eine Skizze)


Gaußbasis — die sehr glatte Variante
Häufig möchte man „schöne glatte“ Kurven erstellen, die nur von sehr wenigen Kontrollpunkten gesteuert werden. Hierzu benutzt man eine Funktionenbasis deren Elemente bereits die gewünschten Eigenschaften („schön“ und „glatt“) besitzen, wie etwa: \[ B_{sg} := \{0.564 \cdot \exp(-(t-i)^2) | i=1,2,3,\dots,k\}. \] (es handelt sich hierbei um Funktionen, \(t\) sind hier Variablen, die \(i\) werden fix gewählt. \(k\) ist am Ende die Anzahl der Kontrollpunkte.)


Uniforme Kubische B-Spline-Basis Uniforme Kubische B-Spline-Basis Uniforme Kubische B-Spline-Basis Uniforme Kubische B-Spline-Basis
B-Spline Basisfunktionen, genau um je eins versetzt auf der t-Achse; es überlappen sich immer vier Stück (die Kurve ist nur schön kontrollierbar, wenn man vier überlappenden Funktionen hat, d.h., vier Kontrollpunkte).


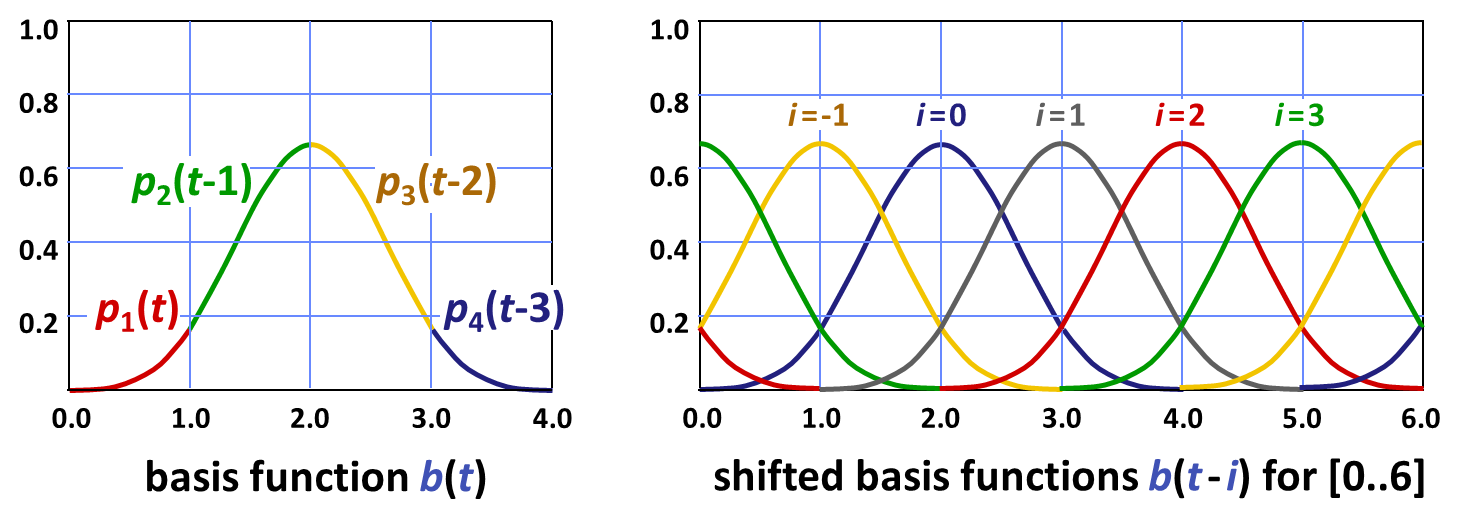
B-Splines — nicht ganz so glatt, aber meistens glatt genug
Statt der Gaußfunktionen können Sie auch die sogenannte „uniforme kubische B-Spline-Basis“ anwenden, die die Gaußfunktionen recht gut approximiert, aber schneller zu berechnen ist.


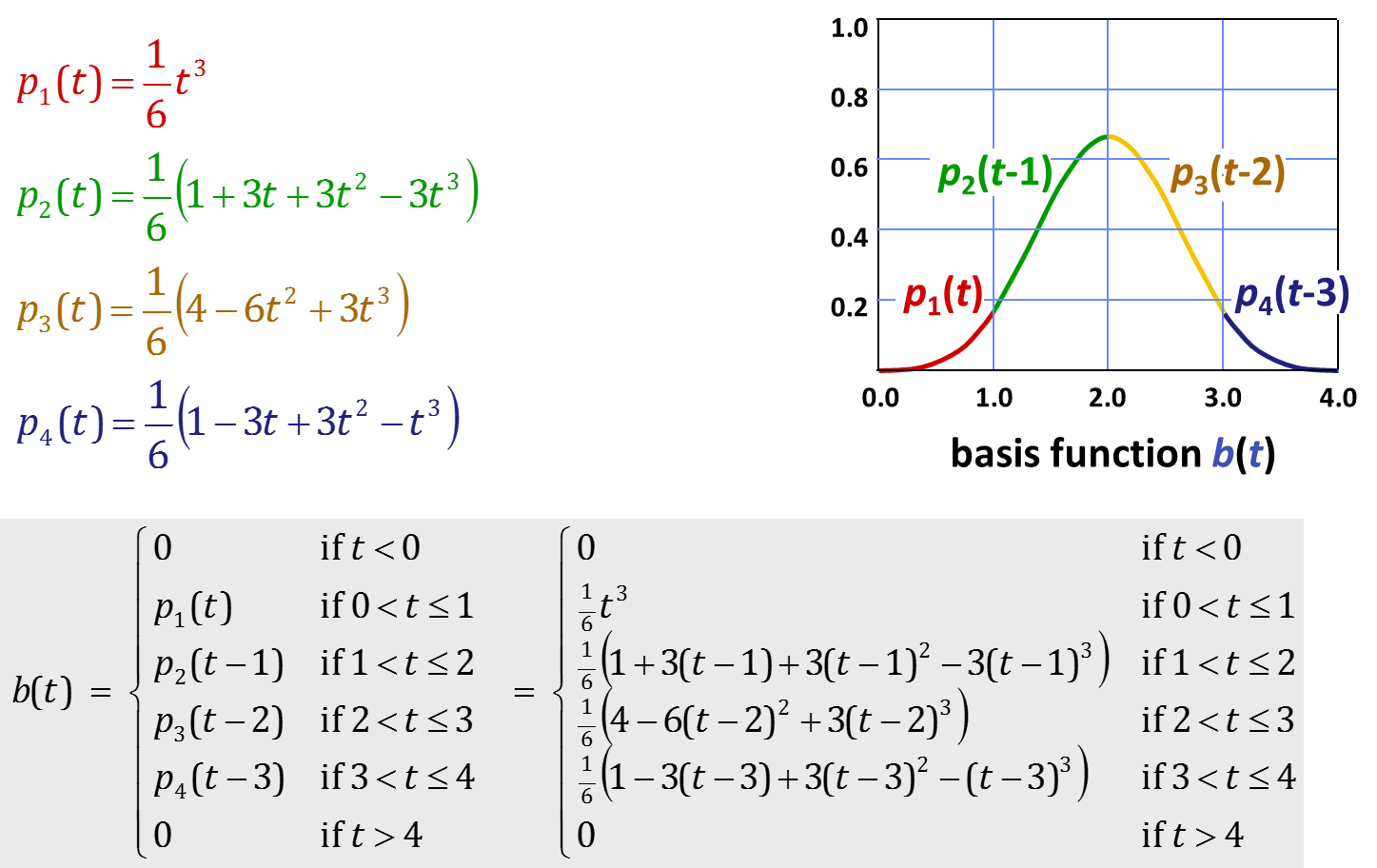
Die Basis lautet dann \[ B_{bspline} := \{b(t-i) | i=1,2,3,\dots,k\}. \] mit B-Spline Basis durch Polynome B-Spline Basis durch Polynome B-Spline Basis durch Polynome B-Spline Basis durch Polynome


Diese sehen fast aus wie die Gauß-Basis, bestehen jedoch aus vier polynomiellen Stücken dritten Grades, was die Berechnung schneller macht und einen praktischen Nebeneffekt hat: der Support, also der Anteil im Definitionsbereich der nicht Null ist, erstreckt sich nur über die Zentren der umliegenden zwei Basisfunktionen.
Bei der Gaußbasis hingegen ist der Support unendlich groß. (Am Ende würde die Kurve bei dieser stets etwas zum Ursprung gezogen, da sich die Funktionen nicht exakt zu eins addieren. Um es richtig zu machen, müsste man bei der Gauß-Basis den Anteil aller Punkte, und nicht nur der umliegenden 4, mit einbeziehen.)


Kurvengestaltung
Ob Sie die eine, oder die andere Basis wählen ist nicht so wichtig. Die wichtige Eigenschaft besteht darin, dass Sie die \(1\)-Funktion auf \(\mathbb{R}\) partitionieren, d.h. die Summe aller Basisfunktion ist genau die \(1\)-Funktion (\(f(t)=1\)) (wobei dies nur bei der Spline-Basis stimmt, die Gauß-Basis summiert nur „fast” zur \(1\)-Funktion, aber für unsere Zwecke genügt es). Indem wir die Auswertung aller Basisfunktionen in den Gitterpunkten \(i=1,2,\dots,k\) so verstehen können, dass der Wert der Basisfunktionen uns angibt wie groß ihr Anteil an dem Funktionswert \(1\) an genau diesem Gitterpunkt ist, ist der Schritt zu einer glatten Kurve im Raum nicht mehr groß. Eine solche Kurve hat die Form \[ f\colon [0,k] \to \mathbb{R}^2, f\colon t \mapsto (x_t, y_t)^T. \] Dabei ist \(t\) der Parameter, der angibt, wie weit man auf der Kurfe „entlanggelaufen” ist (daher spricht man auch von einer parametrischen Kurve). Will man eine solche Kurve nun mit Hilfe einer Basis darstellen, dann sieht das wie folgt aus: \[ f(t) = \sum_{i=1}^{k} P_{i}\cdot b(t-i) \] Hierbei sind die \(P_i \in \mathbb{R}^2\), \(i=1,\dotsc,k\), (Kontroll-)Punkte, welche die Kurve durchlaufen soll. Wichtig hierbei ist, dass die Funktion (für B-Splines) nur im Definitionsbereich \([2,k-2]\) ausgewertet werden sollte. Warum ist dies so?


Übrigens ist die Summe zwar richtig. Um Rechenzeit zu sparen genügt es jedoch, wenn wir für einen gegebenen Auswertungspunkt \(t\) stets nur die umliegenden Basisfunktionen für \(i=\lfloor t\rfloor + j, j=0,1,2,3\) aus. Alle restlichen Basisfunktionen sind im Falle der Gaußbasis entweder vernachlässigbar klein oder im Falle der B-Spline Basis genau \(0\).


Aufgaben

  1. Plotten Sie einige dieser Basisfunktionen, z.B. mit Matplotlib.
    Wie sehen die Funktionen aus?
  2. Benutzen Sie nun diese Basis um eine Kurve zu gestalten, die von wenigen Kontrollpunkten gesteuert wird.
    Wir betrachten hierzu die Basisfunktionen \[ b_i \in B_{sg} \text{ mit } i \in \{2,3,\dots,k-2\},\, k\in \mathbb{N} \] und setzten die Funktion an jedem Punkt stets aus vier Basisfunktionen zusammen. (siehe obenstehendes Bild (rechts)). Das bedeutet wiederum, dass wir stets mindestens 4 Punkte angeben müssen, bevor ein Kurvensegment entstehen kann.

    Schreiben Sie ein PyQt Anwendung (oder mit einem äquivalenten Framework), indem Sie in einem Fenster mehrere Punkte anklicken können, die danach durch eine Spline-Kurve interpoliert werden.

    Die Kontrollpunkte sind dabei die Faktoren der Linearkombination. In der Notation des Hintergrundabschnittes weiter unten, erhält man die roten Punkte \(p_i\) als: \[ p_i = \begin{pmatrix} \lambda_i^{(x)} \\ \lambda_i^{(y)} \end{pmatrix} \in \mathbb{R}^2. \]

Aufgabe 2: Fourier-Basis

Bewertung: 60 Punkte


Erklärungen zur Aufgabe
Statt der „Hutfunktionen” \(b(t)\) aus Aufgabe 1 können wir auch andere Funktionsbasen für unseren Funktionenraum wählen.
Die sogenannte Fourierbasis zerlegt eine Funktion \(f\) in Schwingungen verschiedener Frequenzen: \[ B_{\text{Fourier}} ≔ \left\{ 1,\, \sin(t),\, \cos(t),\, \sin(2 t),\, \cos(2 t),\, \sin(3 t),\, \cos(3 t),\,\dots,\, \sin(k t),\, \cos(k t) \right\} \] Und tatsächlich: jede Wellen-Funktion lässt sich in dieser Basis darstellen.
(Wir hören nach \(2k+1\) Basisfunktionen auf, da wir nur endlich viel Speicher und Zeit zum Berechnen haben, die eigentliche Basis enthält jedoch \(\infty\) viele Funkionen)

Projektion einer Funktion auf die Fourierbasis:
Mit der Fouriertransformation können wir eine Näherung bestimmen, die die Funktion \(f\) in Schwingungen verschiedener Amplituden zerlegt. Die Formel dazu lautet: \[ \lambda_m^{\sin} = \int_0^{2\pi} \sin(mt)f(t)dt,\quad m=1,2,\dots,k \] \[ \lambda_m^{\cos} = \int_0^{2\pi} \cos(mt)f(t)dt,\quad m=1,2,\dots,k \] (man beachte: \(cos(0)=1\))
Rekonstruktion der Funktion aus den berechneten Koeffizienten:
Wir rekonstruieren die Funktion dann wie folgt: \[ f(t) \approx \hat f(t) := \sum_{m=1}^k \lambda_m^{\sin} \sin(mt) + \sum_{m=0}^k \lambda_m^{\cos} \cos(mt) \]
Eigenschaften:
Die Basistransformation auf den Funktionenraum hat einige erstaunliche Eigenschaften.
  • Die oben genannte Formel gibt die beste Approximation, die mit dieser Basis möglich ist. Das heißt, der Abstand von der Originalfunktion \(f\) zur Rekonstruktion \(\hat f\) (gegeben durch das Funktionenraum-Skalarprodukt) kann nicht kleiner sein, wenn nur die ersten \(2k+1\) Basisfunktionen genutzt werden dürfen.
  • Wenn wir statt einer kontinuierlichen Funktion eine Diskretisierung \(t_1,\dots,t_n\) verwenden, bei der wir das Intervall \([0,2\pi]\) in genau \(n=2k+1\) Stützpunkte gleichmäßig aufteilen, dann sind die Formeln oben exakt, es gilt \(f(t_i) = \hat f(t_i),\, i=1,\dots,n\).
    (Die Rekonstruktion muss man wieder genauso an den Stützpunkten abtasten).
  • Koeffizienten mit kleinem Index bilden gröbere Strukturen in der Funktion ab, Koeffizienten mit großem Index feinere.
Vor allem die letzte Eigenschaft wollen wir untersuchen und uns dannach zunutze machen.

Aufgaben

Zuerst schauen wir uns eine stetige 1D-Kurve \(y = f(x) \in \mathbb{R}\) an. Später werden wir dies auf parametrische 2D-Kurven ausweiten. (Im ersten Fall ist die \(x\)-Achse der Laufparameter, im zweiten Fall haben wir eine parametrische Kurve, die sich auch schneiden Kann).


  1. Schreiben Sie ein Programm, mit dem man eine stetige 1D-Kurve \(y = f(x) \in \mathbb{R}\) darstellen kann.

    Hinweis für 1D:
    • Starten Sie am besten mit einem Bitmapbild und stellen Sie sicher, dass in jeder Spalte genau ein Pixel schwarz ist.
    • Speichern Sie die Funktionshöhen am besten als Array \([a_0,\dots,a_\text{breite}]\) ab.
    Hinweis für 2D (später):
    • Speichern Sie die \(x\)- und die \(y\)-Koordinate am besten als separate Arrays \([x_0,\dots,x_\text{breite}]\) und \([y_0,\dots,y_\text{breite}]\) ab.
  2. Wenden Sie nun die diskrete Fouriertransformation auf ihre Kurve an, um die Darstellung Ihrer Funktion als Punkt im Fourierraum zu erhalten.

    Hinweise:
    • Berechnen Sie die diskrete Fouriertransformation, indem Sie die Integrale oben durch Summen von Arrayelementen ersetzen. Mit anderen Worten, sie approximieren die Integrale beispielsweise durch \(\lambda_m^{\sin} \approx \frac{1}{n}2\pi \sum_{i=1}^n \sin(mt_i)f(t_i),\)
    • Die Fouriertransformation ist bereits in NumPy unter der Funktion np.fft implementiert; Sie dürfen auch diese zur Lösung dieser Aufgabe nutzen. (Besser ist es natürlich, eine solche Basistransformation einmal selbst implementiert zu haben.)
    • Für den 2D-Fall können sie einfach beide Koordinaten separat behandeln.
  3. Schauen Sie sich die Transformation als Plot an, und schauen sie, wie verschiedene Kurven (z.B. unterschiedliche schnelle Wellen, per Hand gemalt) in der Fourierdarstellung dargestellt werden.
    Beispielsweise können Sie die ersten \(m\) Signalanteile Ihrer Kurve visualisieren, plotten sie also die \(\lambda_i^{(\sin)} \sin(it)\) bzw. \(\lambda_i^{(\cos)} \cos(it)\).
  4. Wenden Sie nun die Fouriertransformation auf eine 2D-Kurve an, indem Sie die Koordinatenfunktionen unabhängig voneinander transformieren.
    Visualisieren Sie das Ergebnis auf geeignete Art und Weise, und berechnen Sie auch hier die Rekonstruktion („inverse Fouriertransformation“).

    Hinweise:
    • Den Code aus Aufgabe 1 müssen sie dabei kaum verändern.
    • Statt der obigen Summe können Sie auch hierfür die NumPy-Funktionalitäten verwenden (im 2D-Fall wäre dies jedoch nicht np.fft2d. Dies ist für Funktionen gedacht, die zwei Argumente besitzen, eine parametrische 2D-Kurve besitzt jedoch nur einen.).
  5. Filtern der Kurve: Bearbeiten Sie nun durch Manipulation des Ergebnisses die folgenden Aufgaben:
    1. Tiefpassfilter:
      Feinere Details der Kurve werden in den Komponenten der hochfrequenten Basisfunktionen repräsentiert. Um die Kurve zu Glätten, müssen Sie nun die Koeffizienten , \(\lambda_m^{\cos}\), \(\lambda_m^{\sin}\) für steigende \(m\) verringern. Sie sollten hierzu ab einem gewissen \(m\) die Werte auf Null setzen, und als zweites einen langsamen Abfall (linear, oder exponentiell) programmieren.

      Glätten Sie die Kurve, indem Sie
      • die Summe der ersten \(k\) Signalanteile verwenden und die restlichen Komponenten auf \(0\) setzen.
        Dies hat den selben Effekt wie das Aufsummieren der zuvor visualisierten Kurvenanteile.
      • die Komponenten zu den hochfrequenten Basisfunktionen linear verkleinern, \(a_n \leftarrow a_n\cdot \frac{1}{n}\)
      • die Komponenten zu den hochfrequenten Basisfunktionen exponentiell verkleinern, \(a_n \leftarrow a_n\cdot e^{-\frac{1}{n}}\)
      Was können Sie Beobachten?
    2. Hochpassfilter:
      Statt sie zu glätten, können wir die Kurve auch schärfen. Dazu verstärken wir die hochfrequenten Signale gegenüber den niederfrequenten. Probieren Sie das ganze aus Teil (e.1) also nochmal genauso; allerdings sollten Sie nun die hohen Koeffizienten leicht verstärken (z.B. um einen Faktor einstellbar von \(1.01,\dots,2\) ab einem bestimmten \(m\), mit linearem Übergang).

      Wie sieht die Kurve nun aus?
    3. Ersetzen Sie die höheren Koeffizienten der Kurven durch Zufallszahlen mit einer Magnitude, die \(\pm \left|\lambda_m^{(\cdot)}\right|\) entspricht (also gleiche Größenordnung, nur der Wert ist zufällig).

      Was für Ergebnisse bekommen Sie? Übrigens: Dies sollte Ihnen das entfernt bekannt vorkommen (siehe auch: „Fractal Brownian Motion und Perlin Noise“ in Aufgabe 6 des letzten Semesters).
  6. Schauen Sie sich die Fouriertransformation der Basisfunktionen aus Aufgabe 1 an. Variieren Sie die Breite der Gaußglocken (B-Splines) durch eine Transformation \(t\rightarrow c\cdot t,\, c=0.25,\dots,4\).

    Was fällt auf? Können Sie an dieser Stelle eine Vermutung aufstellen, warum man genau diese Funktionen benutzt, um „schön glatte Kurven“ zu konstruieren?

Aufgabe 3: 2D-Fourier-Basis (optional)

Wir wiederholen einen Teil der obigen Aufgaben nun an einem Schwarz-Weiß-Bild. Die Formel für die diskrete Fouriertransformation funktioniert analog auch in 2D, wobei jede Komponente nun die Stärke eines Signals mit zwei Ortsvariablen repräsentiert. (Gerade beim Arbeiten mit Bildern ist der Effekt der jeweiligen Operation im Fourierraum häufig deutlicher sichtbar.)


Fouriertransformation in 2D
Interessanterweise ist die Verallgemeinerung der Fouriertransformation (FT) in den zweidimensionalen Definitionsbereich einfach die Hintereinanderausführung der Fouriertransformationen zeilenweise- bzw. spaltenweise-unabhängig in \(x\)- bzw. \(y\)-Richtung. Das Bedeutet die Ausgabe der FT ist selbst wieder ein Bild der selben Breite und Höhe. Insbesondere verlieren wir dabei keine Information über das Bild, es ist lediglich eine andere Darstellung. Die FT gibt, wie auch im 1D-Fall, zwei Werte/Bilder aus: Real- und Imaginärteil bzw. die \(sin\)- und \(cos\)-Komponenten.


Die niederfrequenten Signalanteile befinden nach der Transformation im Zentrum des Bildes.


Aufgaben


Neben der reinen Bildbearbeitung beinhaltet die 2D-FFT auch Anwendungen wie die Kompression (das JPEG-Dateiformat macht dies sehr ähnlich) oder Rekonstruktion von Bildern mit überlagerten regulären periodisch wiederkehrenden Mustern (Beispiel 1, Beispiel 2, Beispiel forensische Bildanalyse). Beachten Sie hierbei, dass das „ausgrauen“ im Fourierraum dem null-Setzen von Basisfunktionen entspricht. (Negative Werte entsprechen dunklen Pixeln, positive Werte hellen Pixeln.)


Unter

können Sie auch die Ergebnisse anderer Operationen im Fourierraum betrachten.

Hintergrundwissen

Parametrische Kurven
Alle Konzepte, die wir auf diesem Aufgabenblatt kennenlernen, sind für sehr allgemeine Funktionen anwendbar. Um einfache Visualisierungen zu ermöglichen und eine Motivation zu haben, betrachten wir (fast) ausschließlich parametrische Kurven \[ f:[a,b] \rightarrow \mathbb{R}^2 \] Hierbei ist \([a,b]\) ein reelles Intervall, das sogenannte Parametergebiet. Wandert man von \(a\) nach \(b\), fährt die Funktion \(f\) dabei eine Kurve im \(2\)-dimensionalen Raum ab.
Die Kurve kann man als zwei eindimensionale Funktionen \[ f_x:[a,b] \rightarrow \mathbb{R},\\ f_y:[a,b] \rightarrow \mathbb{R} \] auffassen; d.h., eine gewöhnliche 1D \(\rightarrow\) 1D Funktion für die x-Achse, und eine zweite für die y-Achse. In allen Anwendungen auf diesem Blatt werden die Achsenfunktionen in Bezug auf die Rechnungen, die damit durchgeführt werden, im Prinzip als unabhängig voneinander betrachtet (man kann die beiden Teile unabhängig bearbeiten und erhält das gleiche Resultat).

Diskrete Repräsentation
Diskret würden wir eine solche Funktion annähern, indem wir eine Python-Liste (Array) von 2D Vektoren speichern. Jeder Eintrag entspricht einem etwas größeren Parameter (z.B. in Schritten von \(0.01\) von \(a=0\) bis \(b=1.0\)).
Macht man die Schrittweite kleiner, so nähert man eine kontinuierliche Funktion beliebig genau an. Dies zeigt übrigens gut, das kontinuierliche Funktionen näherungsweise als hochdimensionale Vektoren (im Beispiel 200 Zahlen) aufgefasst werden können.
Um eine diskrete Funktion aufzuzeichnen, benutzen wir PyQt Mouse-Move-Events – hiermit kann man mit der Maus auf einem Fenster eine Kurve „aufmalen“; der Parameter entspricht dabei der laufenden Nummer des Events (also im Prinzip der Zeit).

Kontinuierliche Repräsentationen
Eine echte Kontinuierliche Repräsentation erhält man nur, wenn man eine Formel für die Kurve kennt. Z.B. wäre die folgende Kurve kontinuierlich (also eine „echte“ Funktion): \[ f_k(t) = \begin{pmatrix} r\cdot \cos(t) \\ r\cdot \sin(t) \end{pmatrix},\quad a=0,\, b=2pi \] Die Kurve beschreibt, wie schwer zu übersehen ist, einen Kreis.
Auf dem Übungsblatt bauen wir kontinuierliche Funktionen durch Linearkombinationen von Basisfunktionen.
Sei \(B\) eine Menge von Funktionen, \(b_i:[a,b] \rightarrow \mathbb{R}\). Diese haben wir (nach irgendeinem Schema oder Kriterium) bereits fest ausgewählt – wir kennen dafür eine Formel. Dann können wir neue Funktionen durch Linearkombinationen bilden. Z.B. erhalten wir eine Kurve, indem wir sowohl die x-Funktion \(f_x\) wie auch die y-Funktion \(f_y\) aus den (hier den selben) \(b_i\) zusammenbauen: \[ f_x(t) = \sum_{i=1}^k \lambda_i^{(x)} b_i(t),\\ f_y(t) = \sum_{i=1}^k \lambda_i^{(y)} b_i(t) \] Addition und Multiplikation oben sind einfach die von reellen Zahlen (dies ist konsistent mit der Vektor Addition/Multiplikation, falls es sich um Tabellen mit Werten handeln würde; überlegen Sie sich dies nochmal!).

Funktionen als Vektorräume.
Definiert man die Addition und Skalarmultiplikation von Funktionen punktweise (also für jeden Wert von \(t\) einzeln), so erhält man ein Konstrukt, das sich Algebraisch genauso wie geometrische Vektoren verhält. Die Dimension ist nur höher (100D für die Approximation mit einer Tabelle von 100 Werten, \(\infty\)-dimensional für kontinuierliche Funktionen). Ein solches Konstrukt bezeichnet man als Funktionenraum.

Abstände und Winkel
Abstände und Winkel sind für geometrische Vektoren durch Skalarprodukte definiert. Für „geometrische“ Vektoren \(x,y \in \mathbb{R}^d\), \(x=(x_1,\dots,x_d)\), \(y=(y_1,\dots,y_d)\) ist das (Standard-)Skalarprodukt wie bekannt wie folgt definiert: \[ \langle x,y \rangle := \sum_{i=1}^d x_iy_i. \]
Für zwei Funktionen \(f\) und \(g\), die durch (gleich-)lange diskrete Vektoren angenähert sind, behalten wir diese Definition natürlich genauso bei. Macht man einen Grenzwertübergang zu zwei Funktionen \( f_x, g_x:[a,b] \rightarrow \mathbb{R} \) so bilden wir stattdessen das Integral (als Grenzwert der Summe): \[ \langle f_x,g_x\rangle := \int_a^b f(t)g(t)dt. \]
Für zwei Kurven \(f, g: [a,b] \rightarrow \mathbb{R}^2\) definieren wir es genauso \[ \langle f,g\rangle := \int_a^b f(t)g(t)dt, \] wobei die Multiplikation nun ein (normales geometrisches) Skalarprodukt der 2D Vektoren \(f(t),g(t)\) ist. Dies ist übrigens konsistent damit, die beiden Koordinatenfunktionen getrennt zu behandeln und das Ergebnis bloß zu addieren: \[ \langle f,g\rangle = \int_a^b f_x(t)\cdot g_x(t)dt + \int_a^bf_y(t)\cdot g_y(t) dt. \] Überlegen Sie sich nochmal, warum das stimmt! (Tipp: Integration ist „linear“ – man kann Summen aufteilen.)
Die „Länge“ (formal benannt als „Norm“) eines Vektors ist nun definiert als \[ ||f|| := \sqrt{\langle f,f\rangle} \] konsistent mit der Notation für geometrische Vektoren. Genauso sagt man, dass zwei Funktionen \(f,g\) orthogonal aufeinander stehen, falls \[ \langle f,g\rangle=0. \]
Andere Winkel könnte man theoretisch auch definieren (über \(\arccos(\cdot)\)); dies wird aber so gut wie nie verwendet / gebraucht.
Numerisch ist dies alles sehr einfach: Wenn wir eine Approximation einer Funktion kennen, also eine Darstellung als Array von Zahlen, dann behandeln wir diese Arrays einfach wie hoch-dimensionale „geometrische“ Vektoren. Wenn wir Formeln kennen, können wir aussuchen, ob wir die Integrale für das Skalarprodukt analytisch ausrechnen (exakt, aber schwieriger) oder die Funktion in ein hoch genug aufgelöstes Array „diskretisieren“, und dann die angesprochene Lösung als Näherung verwenden (Subtilität: Beim Integral spielt die Länge des Intervalls \([a,b]\) eine Rolle, beim Array nicht; wenn man 100% konsistent sein will, muss man hier noch mit \(\frac{|a-b|}{d}\) gewichten; in vielen Anwendungen spielt das aber keine Rolle).