Institut für Informatik
Markus Blumenstock
Wintersemester 2024/25Mathematische Modellierung am Rechner II
Übungsblatt 3: Raytracing und Monte-Carlo-Integration
Letzte Änderung : 09:41 Uhr, 01 November 2020Abnahmetermin : 05. Dezember 2024




Über dieses Übungsblatt
Auf diesem Aufgabenblatt schauen wir uns nochmals einige geometrische Probleme an (Modellierung von 3D Geometrie). Dazu betrachten wir ein weiteres klassisches Renderingverfahren aus der Computergrafik: das Raytracing-Verfahren.
Retrospektive des letzten Übungsblattes
Auf dem letzten Blatt haben wir Objekte auf schlaue Art und Weise „platt gedrückt“ a.k.a projiziert um 3D Geometrie auf einer 2D-Projektionsfläche darzustellen. Da die Objekte selbst aus einfachen planaren Geometrien bestanden (meistens verwendet man dazu Dreiecke) konnten wir einfach Dreiecke auf der Leinwand positionieren und mussten nur darauf achten, dass die Zeichenreihenfolge der gemalten Geometrie auf die richtige Art und Weise eingehalten wird. (Ferne Objekte sollen von näheren Objekten verdeckt werden.)
Diese Technik ist sehr simpel, hat jedoch auch ihre Nachteile; Beispielsweise ist es schwierig, zwei in einander verschränkte Dreiecke zu zeichnen. Features wie Schattenwurf und Spiegelungen sind dabei noch etwas schwieriger zu implementieren.
Aus diesem Grund schauen wir uns nun ein Renderingverfahren an, das auf solche Features zugeschnitten ist — undgleichzeitig lernen wir etwas darüber, wie man sehr hoch-dimensionale Integrale numerisch lösen kann.
Raytracing
Die Grundidee des Raytracing besteht nun darin, Lichtstrahlen physikalisch zu modellieren. Dazu werden Lichtstrahlen von der Lichtquelle aus in alle Richtungen verschossen. Jedes mal wenn ein Strahl auf ein Objekt auftrifft, wird er wieder in alle Richtungen gestreut (diffuse Materialien) oder nach dem Reflexionsgesetz („Einfallswinkel ist gleich Ausfallswinkel“) reflektiert (spiegelnde Materialien). Dies geschieht so lange, bis der Strahl in die Sensoren der Kamera trifft.
Oder vereinfacht ausgedrückt: statt jedes Objekt zu fragen, in welchen Pixeln es vorkommt, fragen wir jedes der Pixel, welches Objekt es sieht.
Übersicht zu unserem Ansatz:
- Als erstes schreiben wir einen einfachen Raytracer, der eine Szene aus Ebenen, Boxen und Kugeln darstellen kann.
- Danach fügen wir Schattenwurf hinzu.
- In der zweiten Hälfte wenden wir uns der Analysis zu, und schauen uns an, wie man Integrale berechnen kann. Ein einfaches, aber in bestimmten Fällen sehr nützlich und leistungsfähiges Verfahren ist die "Monte-Carlo Integration". Hierbei wird eine Funktion an zufälligen Stellen ausgewertet, um damit den Wert des Integrals zu schätzen. Dieses Verfahren eignet sich besonders gut für Computergrafikanwendungen. Wir benutzen es für die Berechnung von weichen Schatten und "ambient occlusion".
Eins noch vorneweg: Das Verfahren ist wesentlich langsamer als jenes des letzten Übungsblattes. Fangen Sie daher mit einer kleineren Bildgröße an.




Aufgabe 1: Einfaches Raytracing
Bewertung: 15+15+30 = 60 Punkte
Wie oben beschrieben könnte man Lichtstrahlen von der Lichtquelle emittieren lassen bis eine der vielen möglichen Reflektionen im Sensor der virtuellen Kamera aufschlägt. Dies so zu implementieren ist eine schlechte Idee. Warum?
Wenn wir erst einmal davon ausgehen, dass die gesamte Szene gleich hell erleuchtet ist, gibt es einen einfachen alternativen Ansatz. Wir schießen die Lichtstrahlen einfach direkt vom Kamerasensor bzw. direkt durch die Sensoren der Kamera (in unserem Fall sind dies die Pixel des zu befüllenden Bildes) in Blickrichtung. Sobald der Strahl auf ein Objekt trifft, prüfen wir dessen Farbe und malen den Pixel, aus dem der Lichtstrahl emittiert wurde, mit genau dieser Farbe an.
Überlegen Sie sich, warum diese Herangehensweise (in dieser vereinfachten Konstellation) äquivalent zu der vorherigen ist und viel schneller abläuft.
Aufgabe
Schreiben Sie einen Raytracer, der Bilder dadurch erstellt, dass ein Strahl durch jedes Pixel des Bildes geschossen wird und gesucht wird, welches Objekt der Szene als erstes getroffen wird.
Lösen Sie dabei die folgenden Teilprobleme:
Tipp: Man sollte die Aufgaben nicht unbedingt in dieser Reihenfolge bearbeiten; die Gruppierung dient zur Punktevergabe.
- Hilfsfunktionen: Schnitttests
- Ebenen: Überlegen Sie sich, wie man einen Strahl mit einer Ebene schneiden kann. Als Ergebnis möchten wir sowohl den Schnittpunkt als auch den Abstand des Schnittpunktes vom Ursprung des Strahls kennen. Implementieren Sie Ihre Lösung in Python!
- Dreiecke/Quader: Nochmal das ganze: Diesmal möchten wir einen Quader mit einem Strahl schneiden.
Tipp: Am einfachsten ist es, zunächst den Schnitt mit Dreiecken zu implementieren (Erweiterung von Aufgabenteil (i)) und dann Quader aus 12 Dreiecken zusammenzusetzen. - Kugeln: Überlegen Sie sich, wie man einen Strahl mit einer Kugel schneiden kann. Auch hier sind Schnittpunkt und Abstand zum Ursprung des Strahls gesucht. Implementieren Sie auch diese Lösung!
Hinweis: Man kann zwar theoretisch eine Kugel aus vielen kleinen Dreiecken approximativ zusammensetzen, aber diese Lösung ist bei einer Pythonimplementation sehr langsam. Daher sollten Sie hier den Schnitttest mit der Kugel direkt implementieren.
- Primärstrahlen:
Bestimmen Sie die Strahlen, die bei einer Zentralprojektion vom Projektionszentrum (entspricht der Kameraposition) durch jeden einzelnen Pixel verlaufen.
Implementieren Sie eine doppelt-geschachtelte Schleife in Python, die alle diese Pixel abläuft und dafür die Strahlen erzeugt. - Modellierung und Rendering: Nun bauen wir alles zusammen.
- Modellieren Sie zunächst eine einfache Szene, in der ein oder mehrere Quader und ein oder mehrere Kugeln auf einer Ebene stehen.
- Weisen Sie jedem geometrischen Objekt eine eigene Farbe zu.
- Rendern Sie dann die Szene mit Hilfe des Raytracingverfahrens. Dazu müssen alle Objekte der Szene auf Schnitt mit den Primärstrahlen getestet werden; danach wird die Farbe des Objektes ausgewählt, das am nächsten dran liegt. Wenn kein Objekt getroffen wird, wird eine Hintergrundfarbe (frei wählbar) angenommen.
Tipp: Am besten bauen Sie den Raytracer in Ihre Lösung für Aufgabenblatt 02 ein — dann können Sie die Szene komfortabel positionieren und eine interaktive Vorschau sehen, bevor das relativ teure Raytracingverfahren gestartet wird (in Python wird die Berechnung u.U. einige Sekunden dauern).
Beobachtung: In dieser (noch) einfacheren Variante wird der Schnittpunkt selbst noch gar nicht benötigt. Haben Sie bereits hier eine Idee wozu wir ihn später benötigen werden?
Fragen für die Präsenzveranstaltung:
- Wie bestimmt man die Primärstrahlen?
- Wie misst man den Abstand zur Kameraposition entlang des Strahls?
- Insbesondere: Wie kann man verhindern, dass die Kamera nach hinten schaut?
- Wie modelliert man die verschiedenen geometrischen Primitive und wie berechnet man den Schnitt mit diesen?
Aufgabe 2: Spezialeffekte!
Bewertung: 10+10 = 20 Punkte
Das Schöne am Raytracing ist, dass man sehr einfach weitere Beleuchtungs-/Schattierungseffekte einbauen kann. Wir bauen nun Schattenwurf ein.
- Lokale Beleuchtung:
Nehmen Sie an, dass sich in der Szene eine punktförmige Lichtquelle befindet. Nutzen Sie diese Lichtquelle, um die Szene mit einem Lambertschen (diffusen) Beleuchtungsmodell zu beleuchten (dies ist sehr ähnlich zur letzten Aufgabe auf Blatt 02).
Konkret bedeutet dies: Messen sie den Winkel der Strahlen von der Lichtquelle aus zur Oberflächennormalen des Objektes und dunkeln Sie die Farbe entsprechend prozentual ab. - Schattenwurf:
Das Ergebnis der lokalen Beleuchtung ist unrealistisch. Wir müssen wissen, ob das Licht den Punkt, den wir schattieren wollen (Teil 1) überhaupt erreicht. Falls nicht, sollte das Ergebnis schwarz (oder zumindest sehr dunkel, wenn man ambiente Reflektionen als Hintergrundhelligkeit modelliert) sein.
Um zu prüfen, ob ein Objektpunkt (Teil 1) im Schatten liegt, schicken wir einen "Schattenstrahl" (allgemein nennt man diese Strahlen auch Sekundärstrahlen) zur Lichtquelle und schauen, ob dieser Strahl ein anderes Objekt schneidet, bevor er die Lichtquelle erreicht. Ist dies der Fall, so schalten wir das Beleuchtungsmodell aus Teil 1 auf schwarz/dunkel.
Tipp: Ein Problem sind Selbstschnitte des Strahls mit dem ausgehenden Objekt. Ein kleiner Schwellenwert \(\epsilon\) beim Test hilft hier.




Anmerkung: Die hier gezeigte Implementierung diskretisiert Kugeln durch Vierecke (bzw. Dreiecke); dadurch sehen gekrümmte Flächen facettiert aus.
In einer Python Implementation sollte man dies vermeiden - die Rechenzeit wäre zu lang.




Aufgabe 3: Monte-Carlo Integration / Flächenintegrale
Bewertung: 20 Punkte
Achtung: In dieser Aufgabe steigen wir etwas tiefer ein. Bereiten Sie entsprechend Fragen für die Präsenzveranstaltung vor!
Die harten Schatten aus Aufgabe 2 sehen nicht so schön aus. Besser wäre es, eine ausgedehnte, flächige Lichtquelle zu benutzen, die weiche Schatten wirft. Leider müsste hierzu ein hochdimensionales Integral berechnet werden:
Jeder Punkt auf der Lichtquelle sendet einen infinitesimalen Strahl an Licht zum Objektpunkt, und die Gesamtbeleuchtung ergibt sich als Integral über alle Schattenstrahlen (im Prinzip berechnen wir dadurch, wieviel Licht im Durchschnitt ankommt).
Etwas Mathematik:
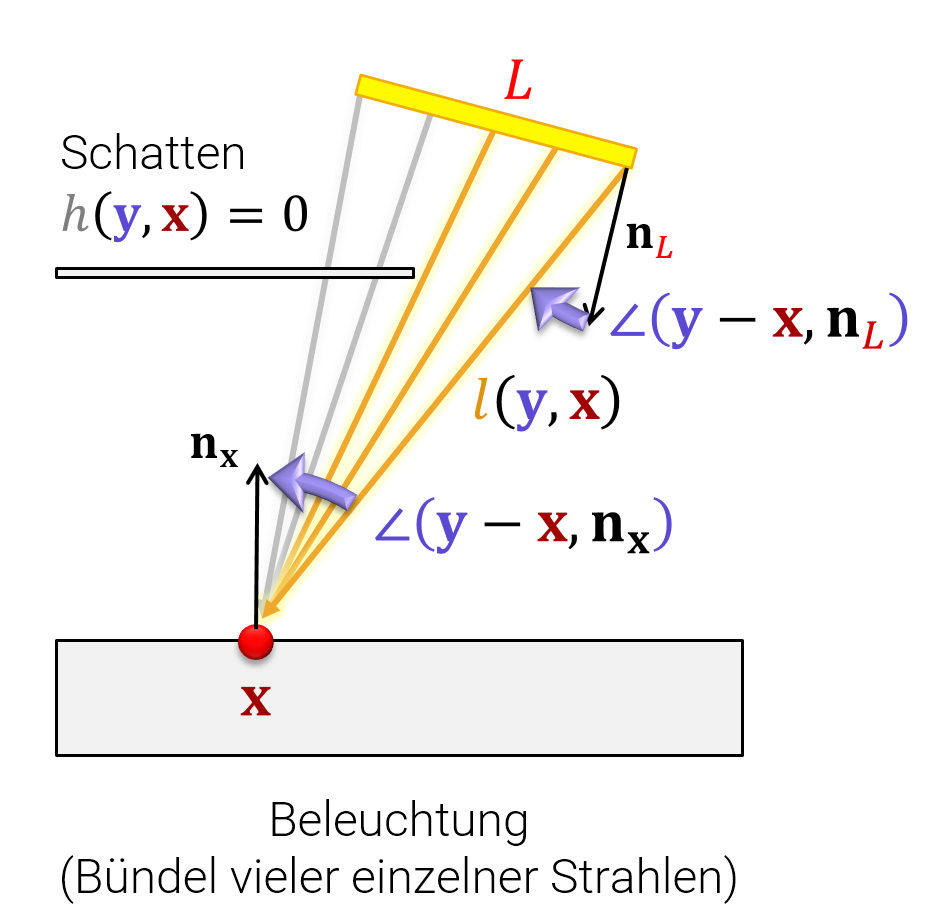
Sei im folgenden \(\mathbf{x} \in \mathbb{R}^3\) ein Objektpunkt und \(L \subset \mathbb{R}^3\) eine flächige Lichtquelle (mathematische ausgedrückt als Menge von Punkten). Weiterhin sei \(l(\mathbf{x},\mathbf{y})\) die Menge an Licht, die entlang eines Strahls von Punkt \(\mathbf{x}\) zu Punkt \(\mathbf{y}\) übertragen wird (hier geht das Beleuchtungsmodell aus Aufgabe 2 ein; Details: siehe unten in den Hinweisen) und \(h(\mathbf{x},\mathbf{y})\) sei \(0\), falls der Strahlengang von einem dritten Objekt blockiert ist ("hidden") und \(1\) sonst. Dann müssen wir folgendes Integral berechnen:
\[ \operatorname{Helligkeit}(\mathbf{x}) = \int_{L} l(\mathbf{y},\mathbf{x}) \cdot h(\mathbf{y},\mathbf{x}) d\mathbf{y} \]
Die einfachste Lösung dafür ist, das Objekt \(L\) mit \(k\in\mathbb{N}\) zufälligen, gleichverteilten Punkten abzutasten und von jedem dieser Punkte einen Schattenstrahl zu schießen. Je größer man \(k\) macht, umso genauer wird das Ergebnis (Beispiel: siehe Abbildung unten), allerdings wird die Rechenzeit auch immer größer.
\[ \int_{L} l(\mathbf{y},\mathbf{x}) \cdot h(\mathbf{y},\mathbf{x}) d\mathbf{y} \approx \frac{|L|}{n} \sum_{i=1}^n l(\mathbf{y}_i,\mathbf{x}) \cdot h(\mathbf{y}_i,\mathbf{x}), \]
wobei die \(\mathbf{y}_i\) zufällige Punkte auf der Fläche \(L\) sind, und \(|L|\) den Flächeninhalt von L bezeichnet (dies ist für Graphikanwendungen egal - dies regelt nur die Helligkeit; bei anderen Anwendungen in der numerischen Mathematik muss man aber aufpassen!).
Tipp: Man kann den Stichprobenpunkt auf der Lichtquelle bei jedem Schattenstrahl unabhängig und von neuem bestimmen; das ist einfacher zu programmieren und vermeidet Kanteneffekte (statt dessen enthält das Bild Rauschen). Schon mit einem (zufälligen) Schattenstrahl kann man dann grob erkennen, wie die weichen Schatten aussehen werden.




Bemerkung: Die hier verwendete Implementation simuliert den oben erklärten Algorithmus mittels Rasterisierung (shadow maps) auf der GPU und läuft in Echtzeit. Der Raytracer in Python wird einige Zeit für die Berechnung brauchen.
Hinweise und Hintergrund zur Lösung
numpy.linalg.solve).Für die Kugeln ist es am einfachsten, wenn man eine implizite Gleichung ansetzt. Für die Kugel im Ursprung des Koordinatensystems mit Radius \(r\) gilt, das alle Punkte \(\mathbf{x}=(x_1, x_2, x_3)^T \in \mathbb{R}^3\) auf der Kugeloberfläche die folgende quadratische Gleichung erfüllen müssen:
\[ Kugel=\{ \mathbf{x} | x_1^2 + x_2^2 + x_3^2 = r^2 \} \]
Setzt man hier eine parametrische Gradengleichung ein, kann man leicht eine quadratische Gleichung in einer Variablen herleiten, die die 0,1 oder 2 möglichen Schnittpunkte beschreibt.
Frage zur Vorbereitung: Versuchen Sie, die Gleichungssysteme für den Schnitt mit der Kugel und dem Schnitt mit der Ebene herzuleiten.
Wie genau fließt Strahlungsenergie zwischen Flächen? Wir können uns vorstellen, dass alle Punkte auf der Lichtquelle mit einem Kontinuum von Strahlen (Strahlbündel) mit dem Empfängerpunkt verbunden sind. Jeder Strahl trägt dabei nur infinetisimal bei (die genaue Definition, die sogenannten Strahldichte [Radiance], ignorieren wir hier; man lernt dies genauer in der Computergraphikvorlesung). Wieviel jeder Strahl beiträgt, hängt von drei Faktoren ab: dem Eingangswinkel (diffuse Beleuchtung: Die Intensität ist proportional zum Kosinus des Winkels zwischen Flächennormale und eintreffendem Strahl) Abstrahlwinkel (auch bei der ausgehenden Fläche gilt das gleiche Gesetz: der Kosinus des Winkels zur Normale bestimmt, wieviele Lichtstrahlen ein Flächenelement verlassen) und dem Abstand (die Intensität nimmt mit dem Quadrat des Abstandes ab, wie alle elektromagnetsiche Strahlung). Man erhält folgende Formel:
\[ l(\mathbf{x},\mathbf{y}) = \frac{cos \angle (\mathbf{x}-\mathbf{y},\mathbf{n}_L) \cdot cos \angle (\mathbf{x}-\mathbf{y},\mathbf{n}_\mathbb{x})}{|| \mathbf{x}-\mathbf{y}||^2 } \]
Die folgende Abbildung illustriert nochmal die Formel (und veranschaulicht auch, warum die stimmt):







Monte-Carlo Integration
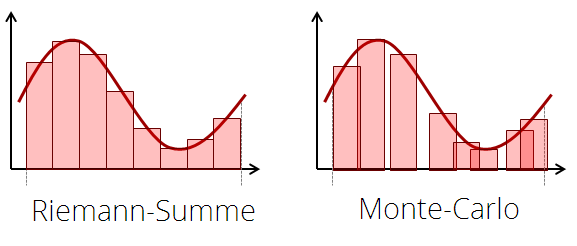
In der Schule (bzw. in leichter Abwandlung in den Grundvorlesungen zur Analysis) lernt man die folgende "Riemannsche" Methode zur Approximation von Integralen:
Sei \(f:[a,b] \rightarrow \mathbb{R}\) eine glatte Funktion. Dann kann man das Integral über die Funktion wie folgt annähern:
\[ \int_a^b{f(x)dx \approx \sum_{i=1}^n \frac{1}{n} f\Big(a+ \frac{(i-0.5) \cdot (b-a)}{n}\Big)} \]
Das heißt, wir nähern das Integral durch rechteckige Balken unter der Funktion an. Je mehr davon wir benutzen, umso genauer wird die Näherung.
Statt dieser Methode können wir auch eine Monte-Carlo-Näherung benutzen:
\[ \int_a^b{f(x)dx} \approx \frac{1}{n} \sum_{i=1}^n{f(x_i)}, \]
wobei \(x_i \in [a,b]\) zufällige, gleichverteilte und unabhängig gezogene Werte aus dem Bereich \([a,b]\) sind. Diese Näherung ist in der Praxis etwas schlechter als die Standardlösung, aber sehr einfach zu programmieren.
Der Große Vorteil liegt darin, dass der Aufwand nicht mit der Dimension des Integrationsgebietes steigt. Wenn man über Flächen integriert, brauchen wir in der ersten Formel bereits \(n^2\) Stützpunkte (was völlig unproblematisch ist). Steigt die Dimension weiter, so wächst der Aufwand der regelmäßigen Abtastung exponentiell mit der Dimension, während das Monte-Carlo-Verfahren davon erst einmal unabhängig ist. Natürlich kann die Lösung durchaus völlig falsch sein (wenn man nicht sehr viele Punkte würfelt); für Funktionen, die wenig schwanken ist die Genauigkeit aber auch in hohen Dimensionen gut. Das Standardverfahren ist dagegen nicht anwendbar. Daher ist Monte-Carlo-Integration für viele Probleme ein wichtiges Verfahren (auch wenn es auf den ersten Blick eher unvernünftig erscheint).
Das Bild unten zeigt die Situation: