Eine hübsche Darstellung des Stanford-Bunnies

I'd like to be known as the person who saw things from a different point of view to others.

Shigeru Miyamoto

Über dieses Übungsblatt

Frameworks, mit denen man 3D-Geometrie mit nur wenigen Zeilen Code oder gar Klicks darstellen kann gibt es wie Sand am Meer. Ziel dieses Blattes ist es zu verstehen, wie die Basis eines solchen Frameworks funktioniert. Konkret schauen wir uns den Mechanismus an, der abstrakte 3D-Geometrie anschaulich repräsentiert und implementieren dazu die Überleitung eines Dreiecksnetzes (mesh) zu einem zweidimensionalen Bild (rendering).
Auf diesem Übungsblatt schauen wir uns an, wie man einen einfachen 3D-Renderer implementieren kann. Das Ganze dient auch dazu, nochmal analytische Geometrie (Beschreibung geometrischer Objekte mit Vektorrechnung) zu üben/vertiefen.
Außerdem macht es Spaß. :-)

Wichtig: Anleitung zur Bearbeitung
Auf diesem Übungsblatt gehen wir problemorientiert vor (wie es die Didaktiker nennen). Konkret heißt das, dass wir auf dem Übungsblatt einige etwas komplexere Aufgaben stellen, zusammen mit einigen Tipps & Hinweisen zur Lösung. Sie müssen sich nun zunächst selbst an einer Lösung versuchen. In der nächsten Vorlesung / Präsenzveranstaltung besprechen wir dann in der Gruppe, wo noch Probleme aufgetreten sind und tragen die verschiedenen Lösungen zusammen. Wichtig ist, schon vor der Präsenzveranstaltung Lösungen auszuprobieren, damit wir in der Veranstaltung sinnvoll diskutieren können.

Aufgabe 1: Ein Retained-Mode Interface für 3D-Graphik

Bewertung: 15+20+15+15+20 = 85 Punkte

Computerspiele können als eine der treibenden Kräfte hinter einigen Errungenschaften der Computergrafik gesehen werden. Dieses zeigt sich unter anderem in der schieren Anzahl an Grafikbibliotheken, die es einem ermöglichen, in sehr einfacher Weise die Grundbausteine einer solchen Engine zusammenzustellen.
Natürlich wollen wir uns nicht damit zufrieden geben, nur fertige "black-box"-Komponenten zu benutzen. Daher programmieren wir selber eine einfache Version einer solchen Bibliothek, die auf dem "immediate mode" Interface von Qt in Form von QPainter aufsetzt.

Die folgende Abbildung zeigt die Schritte unserer Renderingpipeline in einer Übersicht:

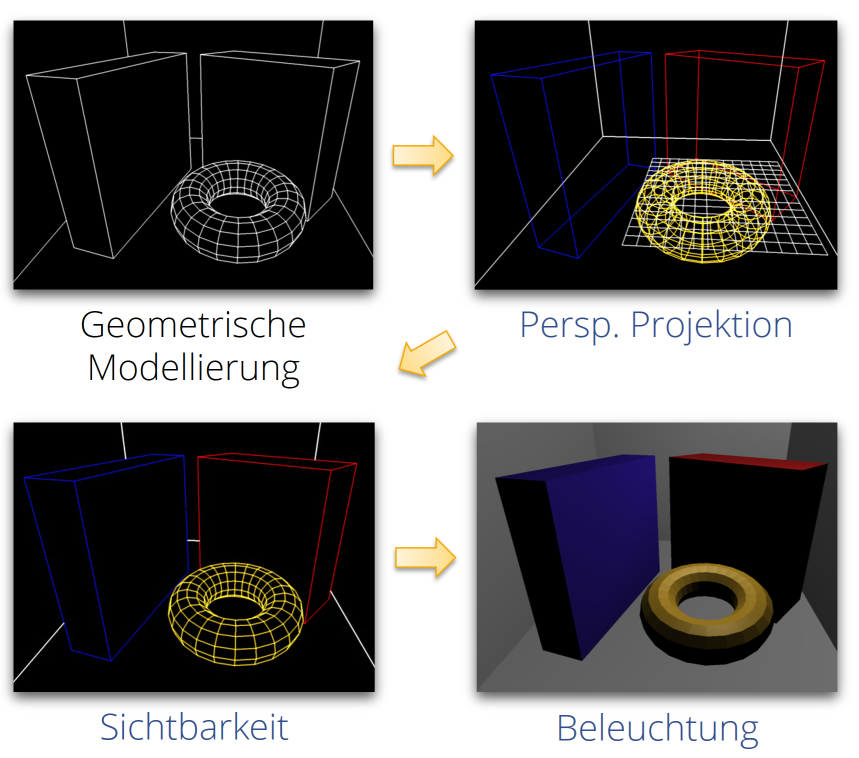
1. Erklärung: Eine einfache 3D Renderingpipeline

Wesentliche Schritte einer 3D Renderingpipeline:

Zunächst wird eine geometrisches Modell erstellt; meistens besteht dies aus Polygonen.
Danach werden diese perspektivisch projiziert. Hier reicht es, die Eckpunkte zu projizieren.
Bevor man die Flächen füllen kann, muss man dafür sorgen, das unsichtbare Flächen entfernt werden. Auf unserem Übungszettel nutzen wir eine einfache Sortierung nach Tiefe.
Danach können die Flächen farbig ausgemalt werden. Wir nutzen der Einfachheit halber zufällige Farben für jedes Polygon.
Das Bild zeigt eine lokale Beleuchtung nach Einfallswinkel der Lichtstrahlen von einer virtuellen Lichtquelle.

Wir schauen uns nun die verschiedenen Schritte im Detail an. Der erste, die geometrische Modellierung, ist in unserem Blatt recht trivial (einfach eine Liste von Polygonen speichern).

Aufgabe 1a: Modellierung

Als erstes müssen wir Objekte geometrisch modellieren. Hierzu machen wir es uns relativ einfach und setzen alle 3D Szenen aus Polygonen zusammen. Ein Polygon ist ein n-Eck, das in unserem Fall 3D Punkte als Ecken hat. Die Punkte sind der Reihe nach mit Linien miteinander verbunden und formen so eine geschlossene Fläche

Entwerfen Sie eine entsprechende Python-Klasse, die eine Liste von 3D Polygonen speichert. Es ist hier sinnvoll, zusätzlich zu den Eckpunkten auch noch für jedes Polygon eine RGB-Farbe zu speichern — damit können wir auch farbige Szenen modellieren.

Nutzen Sie Ihren Code, um ein einfaches 3D Objekt aus Polygonen zu modellieren. Wir empfehlen einen Würfel zu modellieren (6 Flächen). Wenn das gut klappt, können Sie optional versuchen, eine Kugel zu erzeugen, die aus kleinen Vierecken zusammengesetzt ist (das ist etwas komplizierter, aber machbar; probieren Sie das am besten erst, wenn das Rendering schon funktioniert).

Aufgabe 1b: Wireframe-Rendering

Als nächstes müssen wir die Polygone rendern, also eine Ansicht der 3D Szene auf dem 2D Bildschirm darstellen. Die Renderingpipeline ist unten in den Hinweisen zur Aufgabe genauer erklärt.

Schreiben Sie nun Code, der Ihre Szene in einem geeigneten Viewer anzeigt.
Es bietet sich an, eine weitere Python-Klasse zu definieren, die beispielsweise von QWidget abgeleitet ist.
Insgesamt sind zwei Schritte nötig:

Zunächst müssen alle Eckpunkte auf dem Bildschirm projiziert werden. Sie können dazu entweder die Parallelprojektion oder die Zentralprojektion benutzen (mehr dazu in den Erläuterungen unten).
Danach werden die Eckpunkte mit Linien verbunden (man erhält eine Wireframe-Darstellung).

Fragen (Theorie):

Wie funktioniert die 3D-Projektion?
Wie kombinieren wir dies mit der Idee, eigentlich mit einer „Kamera“ in einem virtuellen Raum herumzulaufen? Oder anders gefragt: welche Transformationen sind nötig, damit nachher nur ein bestimmter bzw. gewünschter Ausschnitt der ganzen Szenerie zu sehen ist?
Warum kann man eigentlich 3D-Linien als 2D-Linien mit QPainter zeichnen?

Aufgabe 1c: Animation

Zum Schluss möchten wir die Szene animieren.
Die Aufgabe ist es, den modellierten Würfel sich im Viewer (um eine vorgegebene Achse) drehen zu lassen und das Bild immer neu zu zeichnen.
QTimer bzw. QPropertyAnimation sind hier nützlich. Ihre Szene (z.B. der 3D Würfel) sollte dabei gut im Bild zu sehen sein (auf Zoom und Position achten).

Alternativ können Sie sich auch überlegen, wie man einen interaktiven Viewer bauen könnte, bei dem man z.B. mit der Maus die 3D Szene um verschiedene Achsen drehen kann. Diese Lösung gibt genauso viele Punkte, ist aber optional.

Fragen (Theorie):

Wie wählen und implementieren wir die richtige Drehung?

Aufgabe 1d: Verdeckte Flächen

Statt der einfachen Wireframe-Darstellung wollen wir jetzt gefüllte Flächen zeichnen.
Geben Sie z.B. jedem Polygon eine zufällige 3D Farbe, damit man die Flächen unterscheiden kann. Offensichtlich müssen die Polygone gefüllt gezeichnet werden (Tipp: painter.fillPath(...)). Das alleine reicht aber nicht aus — wir müssen die Sichtbarkeit berücksichtigen. Der einfachste Ansatz ist, die Polygone in einer Reihenfolge von hinten nach vorne zu zeichnen.

Fragen (Theorie):

Wo sind hier die Probleme?
Löst die Sortierung wirklich immer alle Probleme?

Aufgabe 1e: Der berüchtigte Bunny

Würfel (und vielleicht sogar eine 3D Kugel) sind schön und gut, aber was wir eigentlich wollen sind riesige virtuelle Welten. In der Computergrafik dient oft der Stanford-Bunny als Standardobjekt, wenn man keine schönere 3D Szene zur Hand hat, und die Würfel und Kugeln leid ist.

Übrigens — der Bunny ist so etwas wie das Hello World der 3D-Graphik; dabei ist es völlig egal, um welche Art von Anwendung es sich handelt. Diesem Vorbild wollen wir an dieser Stelle folgen.
Alternativ können sie sich aber auch ein anderes Modell aus dem Stanford-Repository für 3D-Scans aussuchen

Vorsicht: Die größeren Datensätze bringen einen einfachen, in Python geschriebenen Renderer ohne GPU-Unterstützung schnell ins Schwitzen. Wir empfehlen Ihnen daher, die Modelle mit der geringsten Auflösung zu verwenden.

Auszug aus einer Beispielspieldatei: bunny.tar.gz/reconstruction/bun_zipper_res4.ply

ply
format ascii 1.0
comment zipper output
element vertex 453
property float x
property float y
property float z
property float confidence
property float intensity
element face 948
property list uchar int vertex_indices
end_header
-0.0312216 0.126304 0.00514924 0.850855 0.5
-0.0446774 0.131204 0.00570479 0.900159 0.5
-0.0683011 0.144828 0.0413688 0.398443 0.5
...
-0.0277717 0.0382563 0.0322865 0.074682 0.5
-0.0179091 0.0385902 0.0296167 0.782021 0.5
-0.0180834 0.0348142 0.0458772 0.143796 0.5
3 164 94 98
3 224 335 49
3 331 350 376
...
3 409 412 410
3 442 445 436
3 435 423 430

Laden Sie sich ein Modell aus dem Stanford-Repository herunter.
Jedes der Archiv enthält jeweils einen Ordner mit Rohdaten der 3D-Scans (data) sowie fertige Meshes (reconstruction). Wir sind natürlich an letzterem Interessiert (die Rohdaten verarbeiten wir gerne noch in einer späteren Vorlesung).
Wir empfehlen Ihnen zu Testzwecken zuallererst die Version geringster Auflösung zu arbeiten. Im Falle des Bunnies wäre dies die Datei reconstruction/bun_zipper_res4.ply.

Die Dateien im Stanford-Repository befinden sich im ply-Format:

Zuerst starten diese Dateien mit einem Header, der mit end_header endet und den Sie beim einlesen bis auf die Zeile
```
element vertex 453,
```
die Ihnen die Anzahl der Eckpunkte angibt, ignorieren können.
Als nächstes folgen die Punktkoordinaten der Dreiecksecken. Es reicht dabei aus, die ersten drei Werte auszulesen, die anderen Werte — confidence und intensity dem Header aus dem Beispiel nach zu schließen — können Sie für diese Anwendung ebenfalls ignorieren.
Nachdem die gesamte Anzahl an Punktkoordinaten eingelesen wurde, folgen die definierten Dreiecke (bzw. $n$-Ecke). Die erste Zahl in jeder Zeile gibt Ihnen an, wieviele Punkte involviert sind, die restlichen Zahlen sind die ids der Punktpositionen, die zusammen ein $n$-Eck bilden.
Wie gesagt, können Sie aber davon ausgehen, dass es sich bei allen rekonstruierten Modellen im Stanford Repository nur um Dreiecke handelt.
Lesen Sie Ihre gewählte Datei im ply-Format ein und zeigen Sie das Modell mit Ihrem Viewer an.

Zusätzliche Erläuterungen zur Aufgabe

2. Erklärung: Perspektivische Projektion

In der Graphik unterscheidet man verschiedene Projektionen.
Orthogonalprojektion: Die einfachste ist eine Parallelprojektion auf die $xy$-Ebene - hier wird schlicht die Tiefenkoordinate ($z$-Koordinate) gelöscht und nur die $x$- und $y$-Koordinaten zur Darstellung benutzt. Fertig.
\[ \left(\begin{array}{c} \text{prj}_x \\ \text{prj}_y \end{array} \right) = \left(\begin{array}{c} x \\ y \end{array} \right) \]
Schrägprojektion: Eine etwas aufwändigere Art der Parallelprojektion ist die Schrägprojektion (auch Kavaliersperspektive genannt). Hier wird die Tiefe durch einen schrägen Versatz angedeutet. Die Berechnung ist einfach — man addiert einfach die z-Koordinaten auf sowohl die $x$- und $y$-Koordinate auf. Um Längen zu erhalten teilt man noch durch $\sqrt{2}$:
\[ \left(\begin{array}{c} \text{prj}_x \\ \text{prj}_y \end{array} \right) = \left(\begin{array}{c} x + \frac{1}{2}\sqrt{2}z \\ y + \frac{1}{2}\sqrt{2}z \end{array} \right) \]
Perspektivische Projektion: Dieser Teil ist interessanter. Hierzu stellt man sich vor, dass wir eine Lochkamera benutzen. Diese funktioniert wie folgt:

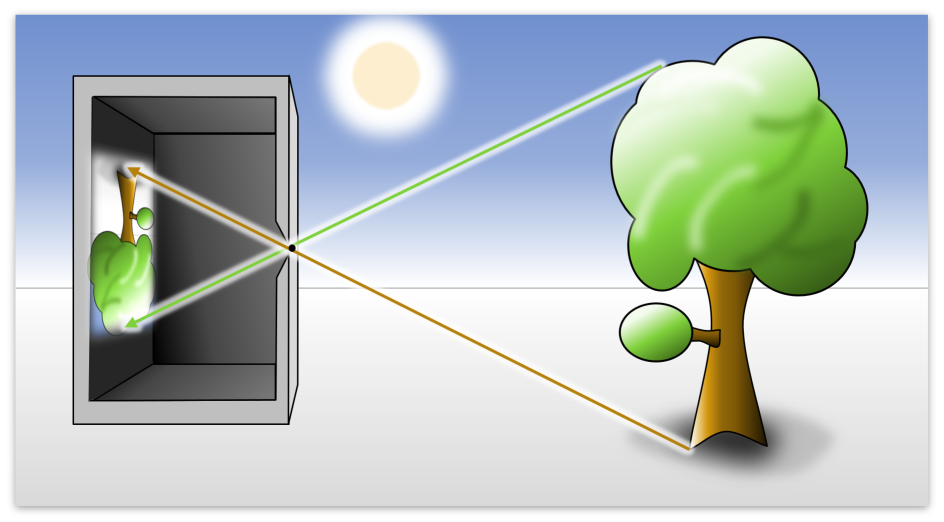
In der Computergrafik benutzt man fast immer das Modell einer idealen Lochkamera: Das Bild entsteht, indem nur Strahlen erlaubt werden, die durch ein Projektionszentrum vom Objekt auf einen flachen Bildschirm gelangen. — Lochkamera

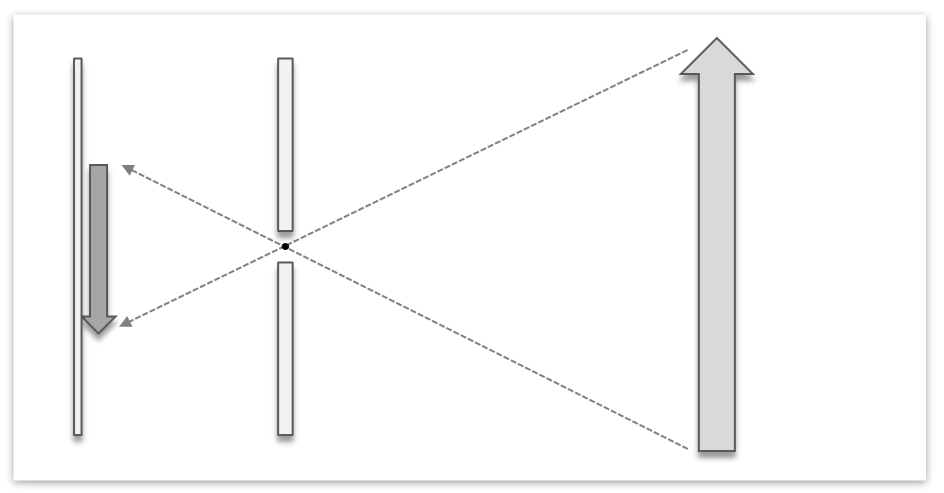
Schematisch sieht das ganze so aus: Wir sammeln die Strahlen, die vom Objekt (rechts) durch ein Projektionszentrum (Mitte) laufen, und schneiden diese mit der Bildebene (ganz links). Dabei wird das Bild gespiegelt (Punktspiegelung) — Lochkamera

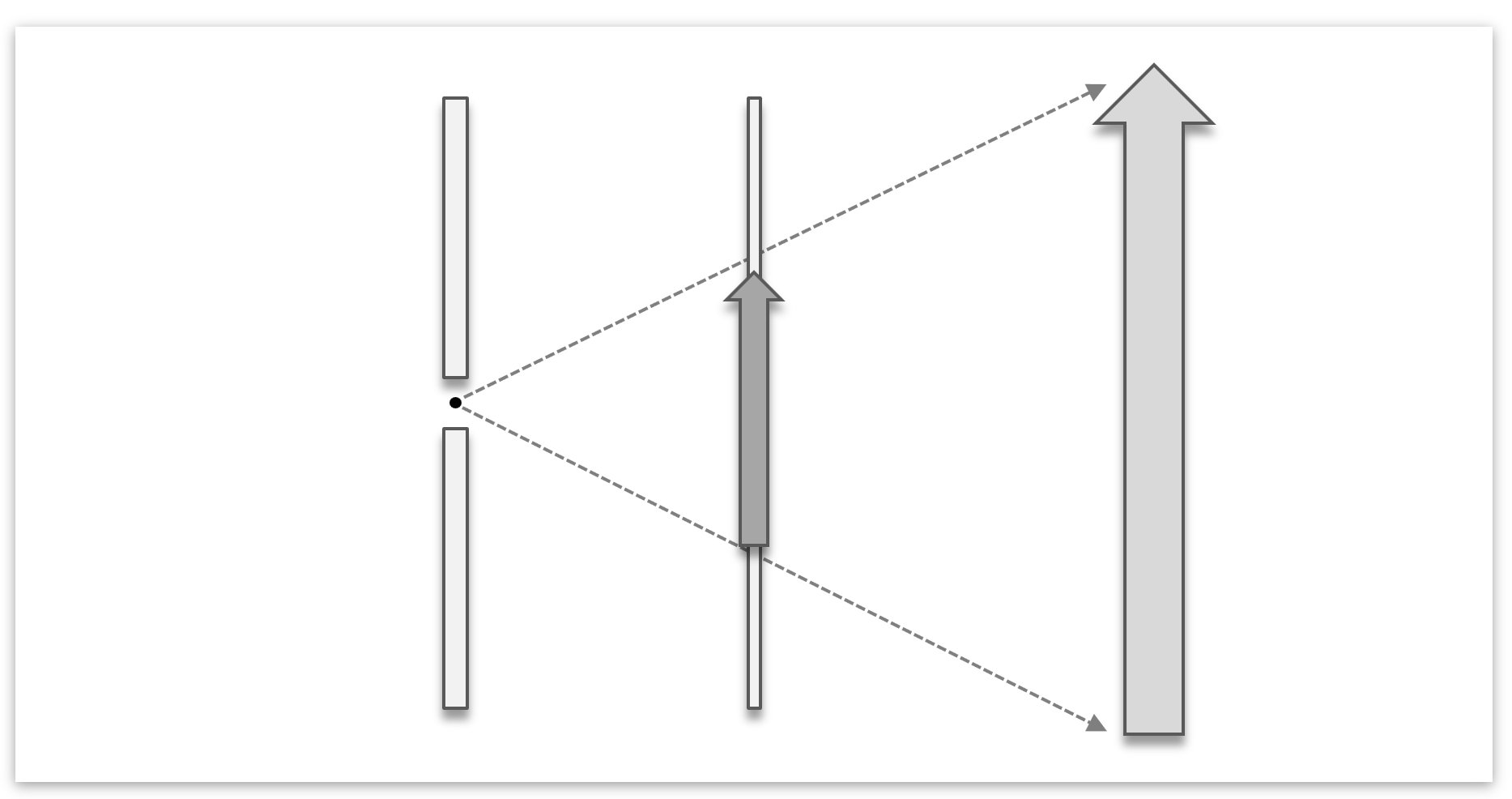
In der Computergrafik kann/ man sich die Spiegelungen sparen, da wir nicht an die Gesetze der Physik gebunden sind. Wir legen einfach die Projektionsebene in den Strahlengang rein (nun in der Mitte). Damit erhalten wir das Modell der *Zentralprojektion*. — Lochkamera

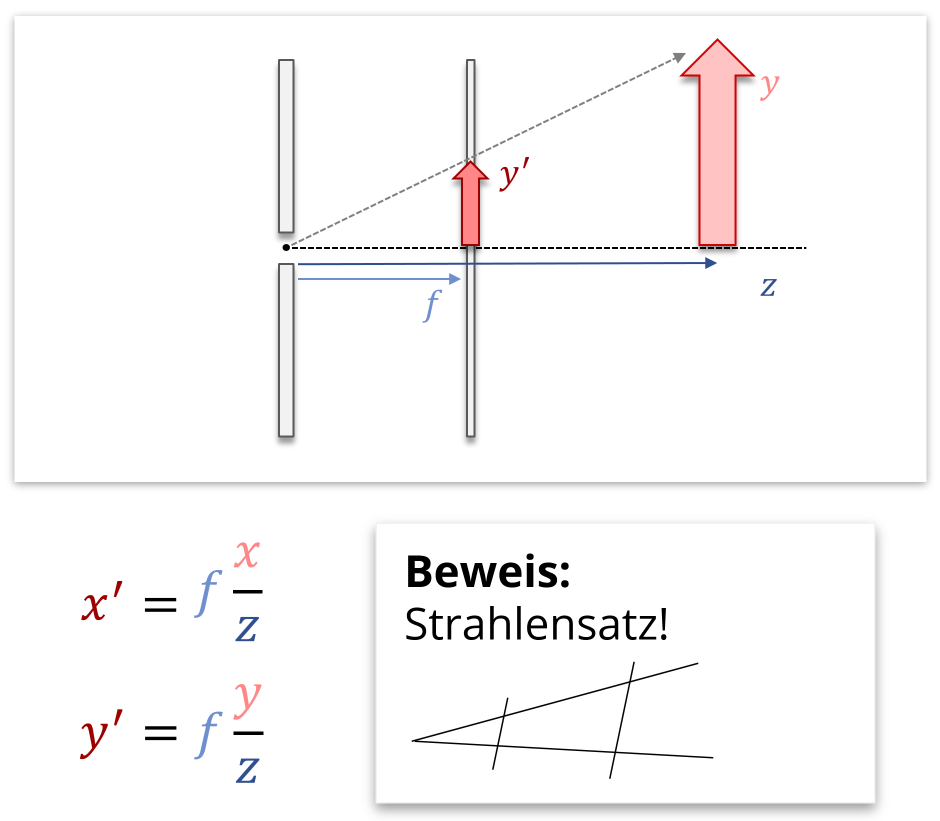
Berechnen können wir dies nun durch Anwendung des Strahlensatzes. Wie zuvor nehmen wir an, dass die Kamera in Richtung
der $z$-Achse schaut, und dass das Projektionszentrum im Ursprung des Koordiantensystems liegt. Danach ergibt sich die
Formel für die Projektion einfach mit dem Strahlensatz.
**Achtung:** Man muss dazu die Szene richtig positionieren / verschieben. Das darzustellende Objekt muss unbedingt vor
dem Projektionszentrum liegen! — Lochkamera

Zusammengefasst lässt sich die perspektivische Projektion also wie folgt berechnen:
\[ \left(\begin{array}{c} \text{prj}_x \\ \text{prj}_y \end{array} \right) = \left(\begin{array}{c} f \cdot \frac{x}{z} \\ f \cdot \frac{y}{z} \end{array} \right), \] wobei z.B. $f=-1$ gewählt werden kann, wenn der Beobachter im Nullpunkt steht und in die negative $z$-Richtung blickt und die Projektionsebene gerade die Ebene $z=-1$ ist.
Die Bilderserie oben erklärt alles Wichtige. Was noch fehlt, ist, die projizierten 3D-Koordinaten richtig in das 2D Bild einzufügen (so, dass die Kamera durch die Mitte des Bildes schaut, und nicht durch die linke obere Ecke). Außerdem müssen wir richtig skalieren, damit alles gut im Bild ist: Der Ausschnitt, den wir auf der Bildebene sehen, sollte etwa einem Öffnungswinkel von +/- 45 Grad gegen das Projektionszentrum haben; sonst sieht das Bild unschön aus. Hierzu benötigen wir nur eine einzige globale Transformation; wir müssen nur den richtigen Ausschnitt aus der 2D Projektionsebene ausschneiden. Überlegen Sie sich für die Präsenzveranstaltung, wie man dies am besten macht!
Zum Schluss noch eine Visualisierung, die den Übergang von der Zentralprojektion in eine Parallelprojektion zeigt:

Orthogonale Projektion und Zentralprojektion — Zu sehen ist der Übergang von der Orthogonalprojektion bei $0°$ zur Zentralprojektion bei $90°$.
Wenn man die Sache weiter verfeinert, landet man am Ende an einer einheitlichen Formulierung mit homogenen Koordinaten; für unser Übungsblatt geht das aber etwas zu weit. Die "Vollversion" gibt es in der Vertiefungsvorlesung "Computergrafik".
**Quelle**: commons.wikimedia.org

3. Erklärung: Homogene Koordinaten im Detail

Homogene Koordinaten bzw. Zentralprojektion (siehe Erklärung 2) sind mathematisch betrachtet sehr interessante Konstrukte:
Im Euklidischen Raum $\mathbb{R}^n$ haben parallele Geraden keinen Schnittpunkt — in einer perspektivischen Abbildung schneiden sich jedoch alle Geraden, die nicht parallel zur Bildebene / Leinwand liegen.
Die Lösung des Problems liegt im Übergang von euklidischen zu homogenen Koordinaten: Einen Punkt $(x,y,z)$ im euklidischen Raum $\mathbb{R}^3$ soll so dargestellt werden, dass ferne Objekte (große Werte für $z$) kleiner dargestellt werden als nahe Objekte ($z\approx 0$). (In unserer Vorstellung soll die $xy$-Ebene als Leinwand dienen.)
Eine Möglichkeit, dies zu erreichen, besteht darin, die $x$- und $y$-Koordinate jeweils durch $z$ zu teilen, \[ \left(x,y,z\right) \Leftrightarrow \left(\frac{x}{z},\frac{y}{z}\right), \text { falls } z>0. \]
Diese Darstellung (die linke Seite des mathematischen Ausdrucks) wird homogene Koordinaten (der rechten Seite) genannt und besitzt einige interessante Eigenschaften.

Eigenschaften der homogenen Koordinatendarstellung

Ein Punkt im zweidimensionalen Raum entspricht einer Geraden in seinen homogenen dreidimensionalen Koordinaten. Eine Gerade im zweidimensionalen Raum entspricht einer Ebene.
Der Punkt „im Unendlichen“ (beliebig tief, nicht beliebig in der $xy$-Ebene) hat eine im Modell existierende Darstellung.
(Im Gegensatz dazu liegt $(\cdot,\cdot,\infty)$ weder in $\mathbb{R}^3$, noch können wir Punkte mit genügend großen Zahlen effizient im Rechner darstellen.)
Parallele Geraden, die nicht parallel zur $xy$-Ebene liegen haben stets einen Schnittpunkt in homogenen Koordinaten.
(Dies führt zu dem typischen Fluchtpunkt-Verhalten, das im perspektivischen Zeichnen verwendet wird.)
In homogenen Koordinaten ist die Hintereinanderausführung von affinen Transformationen eine einfache Matrix-Matrix Multiplikation. (Warum ist dies in heterogenen Koordinaten — also in der linken Darstellung — nicht so?)

Es ist eine sehr gute Übung, diese Aussagen zu beweisen!

Aufgabe 2: ein einfacher Shader

Bewertung: 15 Punkte

Wenn wir das Zeichnen der Dreiecke nicht durch eine zufällige Farbe sondern eine fest vorgegebene Farbe realisieren, können wir nur noch die Umrisse des Objektes erkennen. Was wir eigentlich möchten, sind jedoch schattierte Flächen, wie sie in der Visualisierung weiter oben zu sehen sind. Dies lösen wir, indem wir einen einfachen Shader implementieren:

Dazu schießen wir von der Kamera aus (bei der Parallelprojektion wäre dies in $z$-Richtung) einen Strahl auf jedes Dreieck und messen den Winkel, mit dem er auftrifft.

Hinweis: Um den Winkel zu messen, benötigen Sie lediglich die Normale des Dreiecks, nicht den Auftreffpunkt (diesen zu finden ist schwieriger).

Hinweis: Das Kreuzprodukt zweier Vektoren gibt einen Vektor aus, der senkrecht auf beiden Eingaben liegt. Über die Orientierung des Kreuzproduktes müssen Sie sich dabei keine Gedanken machen.

Hinweis: Der Winkel zwischen Normale und Strahl wird mithilfe des Standardskalarproduktes gemessen.
Da der Winkel einen festen Wertebereich hat, kann die Farbe des Dreiecks von seiner Neigung abhängig gemacht werden.
Zeichnen Sie Dreiecke die mit der Fläche zur Kamera heller ein und dunkeln Sie die Dreiecke stärker ab, je weiter die Fläche von der Kamera weg zeigt.

Fragen (Theorie):

Was muss eventuell bei der perspektivischen Projektion beachtet werden, wenn die Lichtquelle in der Kamera liegt?
Welche Probleme können auftreten, wenn man den Lichtstrahl nicht von der Kamera aus schießen würde? Können wir so leicht Sonneneinwurf simulieren (siehe Bunny)?

Optionale Aufgabe Sphärenflocken

Bewertung: 20 Zusatzpunkte

Die Sphärenflocke kann auch auf dem nächsten Blatt als darzustellendes Objekt wiederverwendet werden.

Aufgabe 3a: - Generierung beliebig¹ glatter Sphären

Wir starten mit einem Tetraeder oder irgendeinem der anderen platonischen Körper (am besten einem mit dreieckigen Flächen, etwa dem Ikosaaeder). Die Koordinaten der Eckpunkte können dabei einfach abgetippt werden:
```
+1.0 +1.0 +1.0
-1.0 -1.0 +1.0
-1.0 +1.0 -1.0
+1.0 -1.0 -1.0
```
Was noch fehlt sind die Flächen, also welche Punkte zusammen ein Dreieck bilden. Dies ist jedoch sehr leicht, es sind nämlich alle möglichen Tripel dieser vier Punkte, also 4 Flächen.
Wichtig ist nur, dass das Zentrum des Körpers der Nullpunkt ist.
Als nächstes unterteilen wir alle Dreiecke in vier gleichmäßige Dreiecke. (Wir fügen dazu in der Mitte jeder Seite einfach einen neuen Eckpunkt ein und verbinden die neuen Eckpunkte einer Fläche durch neue Kanten und erhalten so unsere neuen Flächen.
Zuletzt normieren wir alle Eckpunkte (es reicht aus das für die neuen zu tun) so, dass sie genau Abstand 1 zum Nullpunkt haben.
Wir wiederholen Schritt 2 und 3 so lange, bis die Sphäre "rund" genug ist.

Aufgabe 3b: - Sphereflakes

Nun da wir Kugeln zeichnen können, können wir auch versuchen etwas Interessanteres damit zu bauen: Sphereflake-Fraktale. Keine Angst, wir werden eine vereinfachte Version der oben dargestellten implementieren.

Fraktale können auch in 3D-definiert werden.
Quelle: https://commons.wikimedia.org/wiki/File:Sf6.jpg — Sphereflakes

Starten Sie mit einer Sphäre.
- In allen kanonischen Himmelsrichtungen (oben, unten, Norden, Süden, Westen, Osten) oder noch besser, ellen Eckpunkten des ursprünglichen kanonischen Körpers (siehe Bild), sollen nun angrenzende halb (oder ein drittel/viertel/...) so große Sphären platziert werden, sodass sie sich nur in einem Punkt berühren.
- Dies kann nun rekursiv beliebig oft für alle angehängten Sphären ausgeführt werden.
Implementieren Sie nun die Sphärenflocke.

[1] Beliebig heißt hier: solange der Rechner mitmacht

Institut für Informatik

Markus Blumenstock

Mathematische Modellierung am Rechner II

Übungsblatt 2: 3D Visualisierung