



Institut für Informatik
Markus Blumenstock
Wintersemester 2024/25Mathematische Modellierung am Rechner II
Übungsblatt 1: Datenstrukturen und kürzeste Wege
Letzte Änderung : 09:41 Uhr, 01 November 2020Abnahmetermin : 7. November 2024
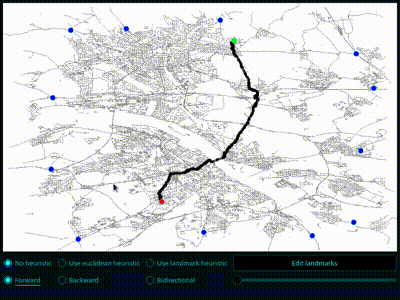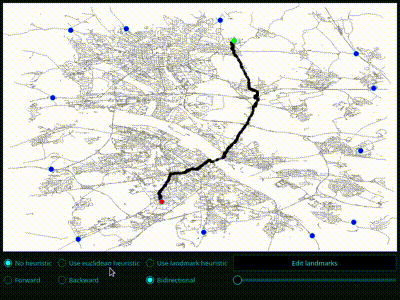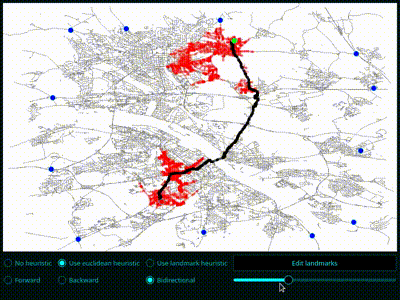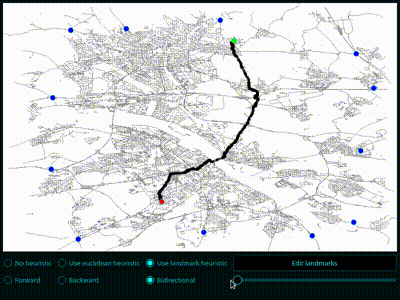



Der zweite Teil des Praktikums "Angewandte Mathematik am Rechner" dient dazu, die praktische Anwendung von Konzepten aus der diskreten Mathematik und linearen Algebra besser kennenzulernen. Dazu schauen wir uns Anwendungen aus der diskreten Optimierung und Geometrie an. Auf diesem Übungsblatt beginnen wir zunächst mit einem bekannten diskreten Optimierungsproblem: das Finden von kürzesten Routen in einem Straßennetzwerk.
Aufgabe 1: Datenstruktur für Graphen.
Aufgabe 2: Einlesen und darstellen von OpenStreeMap-Karten
Aufgabe 3: Die Datenstruktur einer Prioritätswarteschlange
Aufgabe 4: Der Dijkstra Algorithmus
- Implementierung des Algorithmus
- Darstellung des Weges in der Graphik
- Darstellung der besuchten Knoten in der Graphik
Aufgabe 5: Preprocessing, geometrische untere Schranke
- Heuristik, untere Schranke
- Landmark-Algorithmus
Tipp: Wie üblich bauen die Aufgaben aufeinander auf, dennoch können die einzelnen Teile weitestgehend unabhängig von einander gelöst werden. Vergessen Sie nicht, dass Sie eine Gruppe von 3 Personen sind!
Deadline: Dieses Übungsblatt muss in den Übungsgruppen am 7. November 2024 vorgeführt werden. Wie im letzten Semester muss dazu die gesamte Gruppe zu ihrem vereinbarten Abgabetermin (20min Slot) erscheinen, die Lösung vorführen und jedes Gruppenmitglied muss die Lösung erklären können.
Hardware: Falls Sie für die Vorführung keinen eigenen Laptop mitbringen können, sprechen Sie bitte vorher (spätestens am Tag vor der Übung) mit Ihrem Übungsgruppenleiter (oder senden Sie eine E-Mail an Frank Fischer).
Aufgabe 1: Graphen
(20 Punkte)
Einige der grundlegendsten Darstellungsformen zur Modellierung von Beziehungen zwischen Objekten sind Graphen. Mathematisch ist ein gerichteter Graph ein Paar \(G=(V,E)\) bestehend ausführt
- einer Knotenmenge \(V\), z.B. \(V=\{1,2,\ldots,n\}\) und
- einer Kantenmenge \(E \subseteq V \times V\), wobei jede Kante \(e=(u,v) \in E\) eine Verbindung (welcher Art auch immer) vom Knoten \(u\) zum \(v\) beschreibt.
Graphen werden zur Beschreibung verschiedener Beziehungsstrukturen verwendet, z.B.
- Bekanntschaft zwischen Personen
- Freundschaftsbeziehungen in sozialen Netzwerken
- Zuordnungen von Praktikumsteilnehmern zu Gruppen
- Verbindungen zwischen Computern in Netzwerken
- Straßennetzwerke (Knoten sind Kreuzungen, Kanten sind Straßen)
- ...
Auf diesem Übungsblatt wollen wir uns insbesondere mit der letzten Anwendung, den Straßennetzwerken beschäftigen.
Wollen wir mit Graphen im Computern arbeiten, so müssen wir Sie geeignet darstellen. Wie so oft gibt es mehrere Möglichkeiten, einen Graphen im Rechner zu repräsentieren. Welche Darstellungsform die geeignetste ist, hängt von der jeweiligen Anwendung ab. Wir müssen uns daher überlegen, welche (grundlegenden) Operationen wir auf dem Graphen durchführen wollen. Ziel dieser Aufgabe ist es daher, eine Datenstruktur zu implementieren, mit der ein Graph im Rechner dargestellt werden kann.
Aufgabe
- Entwerfen Sie eine Klasse
Graph, welche einen Graphen repräsentiert. Diese soll mindestens die folgenden Operationen ermöglichen:- die Anzahl der Knoten bestimmen
- die Anzahl der Kanten bestimmen
- für jede Kante \(e \in E\) den Start- und den Endknoten bestimmen
- für jeden Knoten \(u \in V\) alle ausgehenden Kanten (d.h. alle Kanten der Art \(e=(u,v) \in E\), \(v \in V \setminus \{u\}\)) sowie alle eingehenden Kanten (d.h. alle Kanten \(e=(v,u) \in E\), \(v \in V \setminus \{u\}\))
- für je zwei Knoten \(u,v \in V\) bestimmen, ob die Kante \((u,v) \in E\) existiert, also ob die beiden Knoten durch eine Kante verbunden sind.
Beachten Sie auch, dass Sie den Graphen erst erstellen müssen (d.h. Sie benötigen vielleicht Funktionen, die neue Knoten bzw. neue Kanten zum Graphen hinzufügen).class Graph: ... def num_nodes(self): ... def num_edges(self): ... def from_node(self, e): ... def to_node(self, e): ... def out_edges(self, u): ... def in_edges(self, u): ... - Implementieren Sie nun den Graphen mittels Adjazenzlisten: für jeden Knoten wird also nur die Liste der ausgehenden bzw. der eingehenden Kanten gespeichert.
- Theoriefrage: Vergleichen Sie die Komplexität der beiden Implementierungen hinsichtlich:
- Speicherbedarf in Abhängigkeit der Größe des Graphen \(G\)
- Zeitbedarf für jede der von Ihnen implementierten Operationen
- Sehr häufig genügt es nicht, nur den Graphen selbst zu kennen. Viele Anwendungen weisen den Knoten bzw. den Kanten gewisse Attribute zu, z.B. Kosten, Längen, Gewichte, Potenziale. Erweitern Sie ihre Klassen um die Fähigkeit, für jeden Knoten bzw. für jede Kante einen Wert zu speichern und wieder abzufragen, z.B.
Wie effizient sind diese Operationen?class Graph: ... def set_node_value(self, u, value): ... def node_value(self, u): return ... def set_edge_value(self, e, value): ... def edge_value(self, e): return ...
Aufgabe 2: Einlesen und Darstellen von OpenStreeMap Karten.
(20 Punkte)
In dieser Aufgabe wollen wir die eben erstellten Graphen dazu nutzen, Straßennetzwerke von OpenStreeMap-Daten einzulesen. Mit anderen Worten, die Knoten \(V\) des Graphen entsprechen gewissen Wegpunkten auf den Karten, die Kanten entsprechen Straßen oder Straßenabschnitten.
Die Kartendaten können mit Hilfe des Skripts download_osm.py runtergeladen werden. Das Skript benötigt vier Parameter in dieser Reihenfolge:
- kleinsten Längengrad
- kleinsten Breitengrad
- größten Längengrad
- größten Breitengrad
Die notwendigen Angaben können auf der Webseite https://www.openstreetmap.org (dort den gewünschten Kartenausschnitt wählen und mittels "Export" die Koordinaten ablesen) bestimmt werden. Um einen Ausschnitt von Mainz/Wiesbaden zu erhalten, kann man etwa den folgenden Befehl ausführen:
python download_osm.py 8.1611 49.9468 8.3781 50.1082
Der Graph wird wie folgt gespeichert:
- die Datei
nodes.csventhält pro Zeile drei mit Komma getrennte Zahlen, die Knotennummer, den Längengrad und den Breitengrad (in dieser Reihenfolge), z.B.:1,8.312332131,50.23132 2,8.312531229,50.23132 - die Datei
edges.csventhält pro Zeile die beiden durch Komma getrennte Knotennummern, die sie verbindet:123,42
Ein Beispielgraph von Mainz/Wiesbaden kann hier runtergeladen werden: nodes.csv, edges.csv.
Tipp: Mit dem Python-Modul csv lassen sich csv-Dateien ganz bequem einlesen.
Tipp: Es ist oft hilfreich, sich kleine Testinstanzen von Hand zu erzeugen, sich also solche Dateien für wenige Knoten und Kanten selbst zu schreiben und daran seine Implementierung zu testen.
Tipp: Die von download_osm.py erzeugten Instanzen enthalten alle Kanten in jeweils beide Richtungen, es gibt also keine Einbahnstraßen.
Abstandsberechnung
(Ein schöne Übersicht ist auch hier zu finden). Ein Problem, das wir haben, wollen wir wirklich kürzeste Wege in Straßennetzen berechnen, ist, dass wir keine Längen für die Kanten (Straßen) haben. Wir kennen nur die Koordinaten der Knoten, genauer ihre Längen- und Breitengrade auf der Erdkugel. Wir müssen aus diesen Informationen also tatsächlichen Längen bestimmen. Je nachdem, wie genau wir das machen wollen bzw. müssen, bieten sich die folgenden Möglichkeiten an:
1. Für kleine Kartenausschnitte kann man vernachlässigen, dass die Erde eine Kugel ist, und sie stattdessen als euklidische Ebene \(\mathbb{R}^2\) auffassen. Jetzt müssen wir nur noch die Gradangaben in Abstände umrechnen.
Breitenkreise haben überall auf der Erdoberfläche immer den gleichen Abstand, nämlich \(111.3\,km\): der Radius der Erde ist \(r_{\text{Erde}}=6378.388\,km\) also ist Umfang gerade \[U_{\text{Erde}} = 2 \pi r_{\text{Erde}} = 40076.594\,km.\] Die Breitenkreise unterteilen den halben Umfang in 180 gleichgroße Abschnitte, also \(40076.594\,km / 2 / 180 = 111.3\,km\).
Der Abstand zwischen zwei Längenkreisen ist nicht immer gleich und hängt von der geographischen Breite ab. Am Äquator beträgt der Abstand ebenfalls \(111.3\,km\), an den Polen hingegen \(0\,km\). Genauer gesagt ist der Abstand genau 1/360 des Umfangs des jeweiligen Breitenkreises. Der Umfang des Breitenkreises lässt sich, wie oben, aus dem Radius berechnen, und der Radius unter Kenntnis des Breitengrades wie in folgender Zeichnung:
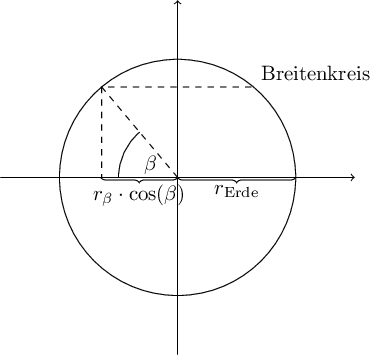



Also für einen Breitengrad \(\beta\) gilt \[ r_{\beta} = \cos(\beta) \cdot r_{\text{Erde}} \quad\text{und}\quad U_{\beta} = 2 \pi r_{\beta}. \] Daher gilt für den Abstand zweier Längenkreise auf Breite \(\beta\) \[ U_{\beta} / 360 = 2 \pi \cdot \cos(\beta) \cdot r_{\text{Erde}} / 360 = \cos(\beta) \cdot 111.3\,km. \] Mit diesem wissen kann man jetzt den Abstand zweiter Punkte \(x_i=(\lambda_i, \beta_i)\), \(i=1,2\) mit Längengraden \(\lambda_i\) und Breitengraden \(\beta_i\) mit dem Satz des Pythagoras ausrechnen. Zunächst schätzen wir den ungefähren Abstand der Längenkreise \[ b := U_{\beta} / 360 \cdot \beta = 111.3 \cdot \cos\left(\frac{\beta_1 + \beta_2}{2}\right) \] (wir haben einfach den mittleren Breitengrad zwischen \(\beta_1\) und \(\beta_2\), also \(\beta = (\beta_1 + \beta_2)/2\), genommen, das sollte ungefähr passen) und wenden dann den Satz des Pythagoras an: \[ \operatorname{dist}(x_1, x_2) = \sqrt{ (b \cdot (\lambda_1 - \lambda_2))^2 + (111.3 \cdot (\beta_1 - \beta_2))^2}. \]




2. Will man es etwas genauer machen, kann man auch die sphärische Geometrie zu Hilfe nehmen. Die wesentliche Idee dabei ist, dass die beiden Punkte \(x_1\) und \(x_2\) zusammen mit dem Nordpol ein (sphärisches) Dreieck bilden. Die Verbindungslinien zwischen zwei Punkten sind dabei "Strecken", die auf einem sog. Großkreis liegen (ein Großkreis ist der Schnitt einer Kugel mit einer Ebene, die durch den Kugelmittelpunkt geht. Alle Längenkreise sind z.B. Großkreise, aber der Äquator ist der einzige Breitenkreis, der ein Großkreis ist). Der Grund, warum man sich für Großkreise interessiert, ist, dass auf einer Kugel die kürzeste Verbindung zwischen zwei Punkten immer auf einem Großkreis liegt (liegen also zwei Städte genau auf dem Äquator, so ist der schnellste bzw. kürzeste Weg zwischen ihnen genau entlang des Äquators).
Zurück zu unserem Dreieck. Von diesem Dreieck kennen wir zwei Kantenlängen: die Längenkreise sind, wie gesagt, Großkreise und der Nordpol liegt auf allen Längenkreisen, also verläuft die Verbindung des Nordpols zu \(x_1\) und \(x_2\) gerade auf dem jeweiligen Längenkreis. Die zugehörige Länge können wir einfach ausrechnen, denn durch den Breitengrad kennen wir ja den Abstand von \(x_i\) zum Nordpol \(N\) entlang des Längenkreises: \[ \operatorname{dist}(x_i, N) = 2 \pi r_{\text{Erde}} \cdot (\pi/2 - \beta_i) / 360^{\circ} = r_{\text{Erde}}\cdot (\pi/2 - \beta_i).\] Außerdem kennen wir noch einen Winkel des Dreiecks, nämlich den am Nordpol. Das ist genau die Differenz der beiden Längengrade. Wie in der Ebene auch genügt für sphärische Dreiecke die Kenntnis von zwei Seiten und dem eingeschlossenen Winkel, um das gesamte Dreieck zu kennen. Wir können jetzt die Länge der dritten Dreieckseite, der Verbindung von \(x_1\) und \(x_2\) mit Hilfe des sog. Seiten-Kosinussatzes ausrechnen: \[\cos(a) = \cos(b) \cdot \cos(c) + \sin(b) \cdot \sin(c) \cdot \cos(\alpha)\] wobei \(a,b,c\) die Seitenlängen geteilt durch den Kugelradius und \(\alpha\) der \(a\) gegenüberliegende Winkel ist. In unserem Fall also: \[\begin{aligned}\cos(\operatorname{dist}(x_1,x_2)) =& \cos(\pi/2 - \beta_1)\cdot\cos(\pi/2 - \beta_2) \\ &+ \sin(\pi/2 - \beta_1)\cdot\sin(\pi/2 - \beta_2) \cdot \cos(\lambda_1 - \lambda_2)\end{aligned} \] Mit ein wenig Vereinfachen (\(\cos(\alpha) = \sin(\pi/2 - \alpha)\) und \(\sin(\alpha) = \cos(\pi/2 - \alpha)\)), Anwenden des Arkus-Kosinus und multiplizieren mit dem Kugelradius erhalten wir: \[ \operatorname{dist}(x_1, x_2) = 6378.388 \cdot \arccos(\sin(\beta_1) \cdot \sin(\beta_2) + \cos(\beta_1) \cdot \cos(\beta_2) \cdot \cos(\lambda_1 - \lambda_2)). \] Das waren zwar ganz schön viele Vorüberlegungen, nur um den Abstand zweier Punkte auszurechnen, aber dafür haben wir am Ende auch eine schicke Formel erhalten, die gar nicht mehr so kompliziert ist, und die wir einfach verwenden können.
Hinweis: Achten Sie darauf, dass die Python-Funktionen math.cos und math.sin den Winkel in Bogenmaß benötigen. Ist \(\alpha\) also ein Winkel in Grad, so wird der Kosinus des Winkels in Python über math.cos(alpha * math.pi / 180) berechnet.
Aufgaben
- Lesen Sie den Graphen aus den Dateien ein. Beachten Sie, dass Sie für jeden Knoten jeweils Längen- und Breitengrad speichern müssen, das wird später noch benötigt.
- Bestimmen Sie für jede Kante die Distanz der beiden Knoten, die sie verbindet (siehe oben).
- Zeichnen Sie nun die Karte mit PyQt. Sie können dazu dieselben Techniken verwenden wie in Aufgabe 6 aus Teil I des Praktikums. Hierzu müssen Sie die Koordinaten der Karte auf Bildschirmkoordinaten umrechnen. Für nicht zu große Kartenausschnitte empfiehlt es sich, die Längen- und Breitengrade einfach als euklidische Koordinaten aufzufassen (also der Längengrad ist die \(x\)-Koordinate, der Breitengrad die \(y\)-Koordinate). Hat hier Fenster z.B. die Breite \(B\) und Höhe \(H\) (in Pixeln), so kann man die kleinsten Längengrade, die im Graphen vorkommen, auf \(0\) und die größten auf \(B\) abbilden (für die \(x\)-Richtung). Ähnlich kann man die kleinsten Breitengrade auf \(0\) und die größten auf \(H\) abbilden. Das folgende Bild illustriert diese einfache Koordinatentransformation:




Diese Transformation soll affin linear sein, d.h. wir suchen eine lineare Funktion \(m_x(x) = a \cdot x + c\), so dass \[m_x(\min \{\lambda_u \mid u \in V\}) = 0\] und \[m_x(\max\{\lambda_u \mid u \in V\}) = B\] ist. Aus diesen beiden Vorgaben kann man leicht die Koeffizienten \(a\) und \(c\) bestimmen. Analog kann man die Transformation für Längengrad \(\mapsto\) \(y\)-Koordinate bestimmen. - Wir möchten später einen kürzesten Weg zwischen zwei beliebigen Knoten bestimmen. Dazu müssen wir festlegen, zwischen welchen Knoten der Weg bestimmt werden soll. Erweitern Sie ihr Darstellungsprogramm so, dass man mittels Mausklick den Konten bestimmen kann, der dem Klick am nächsten liegt. Mit anderen Worten, klickt der Nutzer auf den Pixel \((x,y)\), so wird der Knoten \(u \in V\) gesucht, für den der Abstand zum Pixel \[ \sqrt{ (x - m_x(\lambda_u))^2 + (y - m_y(\beta_u))^2} \] minimal ist (Erinnerung: der Knoten \(u\in V\) wird ja an Pixel \((m_x(\lambda_u), m_y(\beta_u)\)) gezeichnet.
Aufgabe 3: Prioritätswarteschlange
(20 Punkte)
Der Dijkstra-Algorithmus, den wir in der nächsten Aufgabe anschauen wollen, sammelt bereits gesehene Knoten in einer Menge und wählt unter aus dieser stets denjenigen Knoten aus, dessen zugewiesener Distanz-Wert minimal ist. Genauer, sei \(G \subseteq V\) die Menge der "grauen" Knoten (das ist eine Teilmenge, die der Algorithmus verwaltet, siehe unten) und \(d\colon G \to \mathbb{R}\) eine Funktion, die jedem Knoten aus \(V\) einen Wert zuweist, dann müssen wir folgende Operationen durchführen können:
pop_min: Wähle und entferne denjenigen Knoten \(u\) aus \(G\), für den \(d(u)\) minimal ist. Formal: \[ u \in G\colon d(u) = \min \{d(v) | v \in G\}. \]push: Füge einen Knoten \(v \in V \setminus G\) zur Menge \(G\) mit Wert \(d(v)\).decrease_key: Verringere den Wert \(d(v)\) eines Knoten \(v \in G\).
Eine Datenstruktur, die eine Menge darstellt und diese Operationen ermöglicht, heißt Heap oder Prioritätswarteschlange (Priority-Queue) (manchmal wird auch Operation 3 weggelassen, aber wir benötigen sie). In dieser Aufgabe sollen Sie eine Klasse implementieren, die diese Datenstruktur realisiert. Da wir auf recht großen Graphen arbeiten werden ist es wichtig, dass die Implementierung einigermaßen effizient ist.
Ziel ist es also, eine Klasse der folgenden Struktur zur implementieren:
class PQueue:
# Konstruktor
def __init__(self):
...
# Füge Knoten `u` mit Wert `value` hinzu.
def push(u, value):
...
# Verringere den Wert von `u` auf `value`.
def decrease_key(u, value):
...
# Entferne und geben den Knoten zurück, dessen zugehöriger Wert minimal ist.
# Ist die Queue leer, gebe `None` zurück.
def pop_min():
...
Einige Möglichkeiten zur Implementierungen sind die folgenden:
- Die Queue wird als Liste von Paaren dargestellt:
self.items = [(u, 5), (v, 42), (w, 23)]push: diese Operation ist einfach, man hängt einfach das neue Element anself.items.append((u, value)))decrease_key: das ist schwieriger: man muss den Knoten in der Liste suchen und den Wert verändernpop_min: man muss den Knoten mit dem kleinsten Wert in der Liste suchen und ihn aus der Liste entfernen
- Die Queue wird ebenfalls als Liste dargestellt, aber die Einträge werden immer sortiert.
push: das Element wird angehängt und die Liste nach dem zweiten Wert sortiertdecrease_key: wiepush, nur das man zuvor das Element finden musspop_min: das kleinste Element ist das erste der Liste
Besonders interessant sind hier die Operationenpushunddecrease_key: da alle Knoten bis auf den neuen (push) bzw. den mit dem veränderten Wert (decrease_key) bereits sortiert sind, kann man den einen Knoten mittels einerInsertion-SortOperation an die richtige Stelle bringen:# u ist der einzusortierende Knoten # value ist sein Wert # j ist sein Index in der Liste `self.items` # schiebe solange das vorhergehende Element # eine Position nach hinten, solange es einen # größeren Wert als `value` hat while j > 0 and self.items[j-1][1] > value: self.items[j] = self.items[j-1] # Element eine Position nach hinten schieben j -= 1 # Der Knoten `u` gehört nun an Position `j` self.items[j] = (u, value) - Die Queue wird genau wie in 2. dargestellt, aber man speichert zusätzlich in einem
dictdie Information, an welcher Position ein Knotenusich befindet:self.positions[u] = i. Das ermöglicht es, beidecrease_keydie Position des Knotens, dessen Wert man verringern möchte, direkt zu finden.
Achtung: Bei dieser Variante müssen Sie dafür sorgen, dass die Information inself.positionsimmer aktuell ist. Insbesondere muss die Information aktualisiert werden, wenn Knoten bei der "Insertion-Sort" Operation verschoben werden.
Ein zweites Problem ist die Operationpop_min: das Löschen des ersten Elements aus einem Array ist teuer (das gesamte Array muss kopiert werden). Eine Idee, dies zu umgehen, ist, sich die Position des ersten, noch nicht entfernten Elements der Liste zu merken: das erste, noch nicht entfernte Element steht also nicht an Position 0 sondern an Positionself.first. Wirdpop_minausgeführt, wird einfachself.first += 1um Eins erhöht. - Es gibt noch weitere, clevere Datenstrukturen, die Sie verwenden können, und die Sie vielleicht in anderen Vorlesungen bereits kennengelernt haben, z.B. Suchbäume, Binary-Heaps, Fibonacci-Heaps. Diese dürfen Sie natürlich auch verwenden, aber sie sind meist recht aufwendig.
Aufgaben:
- Implementieren Sie die Prioritätswarteschlange auf mindestens eine Art und Weise.
- Theoriefrage: Schätzen Sie für jede Operation ab, wie lange sie in Ihrer Implementierung braucht
Tipp: Diese Aufgabe ist nicht ganz einfach. Nutzen Sie daher die Möglichkeit, in der Vorlesung Fragen zu stellen!
Aufgabe 4: Kürzester-Wege-Algorithmus
(20 Punkte)
In dieser Aufgabe wollen wir einen der wahrscheinlich am häufigsten verwendeten kombinatorischen Algorithmen implementieren: den Dijkstra-Algorithmus zur Bestimmung von kürzesten Wegen in einem Graphen. (Den Algorithmus werden Sie in anderen Vorlesungen wahrscheinlich kennenlernen oder haben es bereits. Wir wollen den Algorithmus hier auch gar nicht analysieren, sondern nur anwenden).
Gegeben ist ein (gerichteter und ungerichteter) Graph \(G=(V,E)\) mit nicht-negativen Kantenlängen \(d \in \mathbb{R}^E\) (die Voraussetzung "nicht-negativ" ist für den Dijkstra-Algorithmus wichtig und nicht in jeder Anwendung gegeben. Für Straßennetzwerke aber ist die Annahme, dass alle Längen >= 0 sind natürlich sinnvoll). Der Dijkstra-Algorithmus dient zur Berechnung von kürzesten Wegen von einem Startknoten \(s \in V\) zu allen anderen Knoten, wobei die Länge eines Weges die Summe der Kantenlängen ist (also nicht die Anzahl der Kanten ist entscheidend, wie bei der Breitensuche, sondern ihre Längen). Er funktioniert wie folgt:
Eingabe: Graph \(G=(V,E)\), Kantenlängen \(\ell \colon E \to \mathbb{R}\), Startknoten \(s \in V\), Zielknoten \(t \in V\).
Ausgabe: Folgen von aufeinander folgenden Kanten \(e_1, e_2, \ldots, e_k\), wobei \(e_1\) in \(s\) beginnt und \(e_k\) in \(t\) endet.
Hilfsvariable:
- die Menge der grauen (schon gesehen, aber nicht besuchten) Knoten \(G \subseteq V\)
- die Menge der schwarzen (schon besuchten) Knoten \(S \subseteq V\)
- für jeden Knoten \(u \in V\) eine Distanz \(d_u \in \mathbb{R} \cup \{\infty\}\)
- für jeden Knoten \(u \in V\) eine eingehende Kante \(p_u \in E\) mit \(p_u = (v,u)\) für einen (Vorgänger-)Knoten \(v \in V\) oder None (falls \(u\) nicht erreichbar ist)
Algorithmus:
- \(G \gets \emptyset\), \(S \gets \emptyset\)
# färbe alle Knoten weiß = (nicht schwarz oder grau) - \(p_u \gets \text{None}\) für alle \(u \in V\)
# keine Vorgänger bisher - \(d_u \gets \infty\) fur alle \(u \in V\)
# kein Weg bisher - \(G \gets G \cup \{s\}\), \(d_s \gets 0\)
# Startknoten grau färben - Solange \(G \ne \emptyset\)
- Wähle \(u \in G\) mit \(d_u = \min \{d_v | v \in G\}\)
# wähle grauen Knoten mit d_u minimal - \(G \gets G \setminus \{u\}, S\gets S \cup \{u\}\)
- Falls \(u = t\), BREAK.
- Für alle Kanten \(e=(u,v) \in E\) mit \(v \notin S\):
- Falls \(v \notin G\)
# v ist weiß -> wird zum ersten mal gesehen- \(G \gets G \cup \{v\}\)
- \(d_v \gets d_u + \ell(e)\)
# queue.push(v, d_u + l(e)) - \(p_v \gets e\)
- Sonst, falls \(d_u + \ell(e) < d_v\)
# es wurde besserer Weg zu v gefunden- \(d_v \gets d_u + \ell(e)\)
# queue.decrease_key(v, d_u + l(e)) - \(p_v \gets e\)
- \(d_v \gets d_u + \ell(e)\)
- Falls \(v \notin G\)
- Wähle \(u \in G\) mit \(d_u = \min \{d_v | v \in G\}\)
- Falls \(d_t = \infty\), return "Kein Weg gefunden"
- \(P \gets []\), \(u \gets t\)
# P ist eine Liste der Kanten auf dem Weg von u nach t - Solange \(u \ne s\)
- \(P \gets P + [p_u]\)
# P.append(p_u) - Mit \(p_u = (v,u)\), setze \(u \gets v\)
- \(P \gets P + [p_u]\)
Aufgaben
- Implementieren Sie den Dijkstra-Algorithmus.
- Erweitern Sie ihr Programm so, dass der Nutzer zwei Knoten auswählen (d.h. anklicken) kann, zwischen denen der kürzeste Weg berechnet werden soll. Außerdem soll der gefundene kürzeste Weg angezeigt werden (z.B. durch Färben der Kanten).
- Erweitern Sie ihr Programm so, dass auch alle vom Algorithmus besuchten Knoten angezeigt werden (z.B. durch eine andere Farbe), das sind also alle Knoten, die am Ende des Algorithmus schwarz oder grau gefärbt sind. Was beobachten Sie?
- Bonus: Erweitern Sie ihr Programm so, dass jeweils die besuchten Knoten nach \(i\) Iterationen angezeigt werden, so dass man den Fortschritt des Algorithmus sehen kann (siehe auch die Animation am Anfang dieses Blattes).
Tipp: Die Mengen \(G\) und \(S\) sowie die Distanzen \(d_u\) und die eingehenden Kanten \(p_u\) lassen sich am besten mittels eines Python Dictionarys dict umsetzen.
Aufgabe 5: Beschleunigung des Algorithmus
(20 Punkte)
In der Praxis ist die Berechnung von kürzesten Wegen unheimlich schnell, selbst auf nicht-so-sehr-schnellen Computern wie Navigationsgeräten. Wir wollen uns in dieser Aufgabe Techniken anschauen, mit den die Berechnung sehr stark beschleunigt werden kann.
Der Dijkstra-Algorithmus wählt unter den noch nicht besuchten Knoten aber in einem Schritt erreichbaren Knoten (den "grauen") denjenigen aus, der dem Startknoten \(s\) am nächsten liegt. Was dabei nicht berücksichtigt wird ist der Abstand zum Zielknoten \(t\). Genau genommen besucht der Algorithmus alle Knoten in der gleichen Reihenfolge, egal welcher Knoten der Zielknoten ist (der Zielknoten beeinflusst nur, wann der Algorithmus stoppt). Wenn wir eine Karte betrachten, dann "sehen" wir aber, dass es keinen Sinn macht, vom Startknoten \(s\) etwa in die entgegengesetzte Richtung zu laufen. Wir wollen den Dijkstra-Algorithmus so anpassen, dass er auch "die Richtung zum Ziel" bei der Suche nutzt.
Eine sehr wirkungsvolle Idee ist, die Entfernung zum Ziel nach unten abzuschätzen. Nehmen wir an, wir dass wir für jeden Knoten \(u\) eine untere Schranke \(h_u\) für die Entfernung zum Ziel \(t\) kennen, dann können wir die Auswahlregel des nächsten Knoten \(u\) in Schritt 5.1 des Algorithmus so verändern, dass diese vermutete Distanz auch berücksichtigt wird:
- Wähle \(u \in G\) mit \(d_u + h_u = \min \{d_v + h_v | v \in G\}\)
# wähle grauen Knoten mit d_u + h_u minimal
Statt die Auswahlregel so zu verändern, kann man sich auch des folgenden Tricks bedienen (dass da wirklich dasselbe Ergebnis rauskommt kann man zeigen, wollen wir hier aber nicht tun): Statt der Kantenlängen \(\ell((u,v))\) verwendet man die Kantenlängen \[\ell^h((u,v)) := \ell((u,v)) + h_v - h_u.\] Wir addieren also auf jede Kante \(e=(u,v)\) zur ihrer Länge den Wert \(h_v\) des Zielknotens \(v\) hinzu und ziehen den Wert \(h_u\) des Startknotens \(u\) ab. Das macht man natürlich nicht für alle Kanten des Graphen (das würde zu lange dauern, weil wir dazu ja jede Kante des Graphen anschauen müssten, was wir gern vermeiden wollen), sondern indem man die Zeilen 5.4.1.2, 5.4.2 und 5.4.2.1 des Algorithmus anpasst, z.B. \[d_v \gets d_u + \ell(e) + h_v - h_u.\]
Bestimmung von unteren Schranken
Eine Frage ist nun, wie kommt man zu diesen unteren Schranken \(h_u\)? Hier können wir ausnutzen, dass wir keinen beliebigen Graphen haben sondern ein Straßennetz.
- Eine einfache untere Schranke ist z.B. die Luftlinie: sicher ist jeder Weg über Straßen von \(u\) zu \(t\) mindestens so lang wie die Luftlinie. Und die Luftlinie ist leicht zu berechnen (nämlich der Abstand der beiden Knoten gemäß Aufgabe 2 dieses Blattes), also \(\operatorname{dist}(u,t)\).
Diese Methode ist sehr einfach, hat aber einige Nachteile. Zunächst einmal funktioniert sie nur gut für Längen, aber nicht für andere Distanzmaße wie z.B. Fahrzeit (was ist die Fahrzeit der Luftlinie?). Ein anderer ist, dass geographische Barrieren (z.B. Flüsse, Berge) zu einem deutlichen Unterschied zwischen der Luftlinie und der tatsächlichen kürzesten Distanz führen können (auf Straßen muss man die Barriere umfahren). Daher wurden andere Methoden entwickelt. - Eine bekannte Methode sind sogenannte Landmarken (Landmark-Algorithmus). Die Idee ist die folgende: man wählt einige wenige Knoten aus (die Landmarken) und berechnet die Längen der kürzesten Wege von allen Knoten zu jeder Landmarke mit dem gewöhnlichen Dijkstra-Algorithmus. Für jeden Knoten speichert man dann diese Distanzen. Wählt man z.B. 10 Landmarken, so muss man für jeden Knoten 10 Zahlen speichern (das ist immer noch sehr wenig im Vergleich dazu, für jeden Knoten die Distanzen zu allen anderen Knoten zu speichern). Sei \(\mathcal{L} \subseteq V\) die Menge der Landmark-Knoten. Dann ist für jeden Knoten \(u \in V\) und jede Landmarke \(L \in \mathcal{L}\) eine untere Schranke für die Distanz zu \(t\) gegeben durch \[\operatorname{dist}(u,t) \ge \max\{0, \operatorname{dist}(u,L) - \operatorname{dist}(L,t) \}\] Dabei ist zu beachten, dass die Abstände von \(u\) zu \(L\) und \(L\) zu \(t\) schon bekannt sind, sie müssen also nicht neu berechnet werden. Da jede Landmarke \(L \in \mathcal{L}\) eine andere Schranke liefert, können wir auch die beste davon nehmen, also \[h_u = \max \{ \max\{0, \operatorname{dist}(u,L) - \operatorname{dist}(L,t) \} \mid L \in \mathcal{L}\}.\] Der Landmark-Algorithmus beschleunigt das Verfahren also, indem in einem Preprocessing Schritt die Abstände jedes Knoten zu jeder Landmarke berechnet werden. Dieser Schritt kann auch einige Zeit dauern, aber das ist nicht schlimm, denn das muss man nur einmal machen (dazu kann man auch Parallelrechner einsetzen). Dann werden diese Distanzen gespeichert (wozu man etwas mehr Speicher benötigt). Will man nun einen kürzesten Weg bestimmen, dann braucht man nur noch auf diese gespeicherten Werte zurückzugreifen und kann die Wegesuche so stark beschleunigen.
Aufgaben
- Implementieren Sie den veränderten Dijkstra-Algorithmus mit euklidischen Distanzen. Zeichnen Sie, wie zuvor, den gefundenen kürzesten Weg und die besuchten Wege. Was beobachten Sie?
- Theoriefrage: Wieso ist durch obige Formel beim Landmark-Algorithmus eine untere Schranke für die Distanz von \(u\) zu \(t\) gegeben?
- Implementieren Sie den Landmark-Algorithmus. Die Landmark-Knoten dürfen Sie vorher "von Hand" wählen oder Sie erweitern Ihr Programm so, dass der Nutzer die Landmark-Knoten durch Klick auswählen kann. Zeichnen Sie, wie zuvor, den gefundenen kürzesten Weg und die besuchten Knoten. Was beobachten Sie?
Tipp: Sie müssen für jeden Landmark-Knoten die Abstände zu allen anderen Knoten bestimmen. Es ist natürlich sehr aufwendig, für jedes Knotenpaar \((u,L)\) bestehend aus einem Knoten \(u\) und einer Landmarke \(L\) einmal den Dijkstra-Algorithmus durchzuführen. Glücklicherweise müssen Sie das aber nicht: wenn man den Dijkstra-Algorithmus ohne Zielknoten mit dem Landmark-Knoten \(m\) als Startknoten startet, dann läuft der Algorithmus so lange, bis er keinen Knoten mehr findet. Am Ende steht dann in \(d_u\) für jeden Knoten \(u\) der Abstand zum Landmark-Knoten. Mit anderen Worten, der Dijkstra-Algorithmus kann also den Abstand von einem festen Startknoten \(m\) zu allen anderen Knoten in einem einzigen Durchlauf berechnen. Das bedeutet, Sie müssen zur Berechnung der Landmark-Distanzen den Dijkstra-Algorithmus nur ein Mal für jeden Landmark-Knoten durchführen.