Analysis I - Integrale & Ableitungen

In diesem Kapitel gibt es eine sehr kurze Zusammenfassung der wichtigsten Begriffe aus den Grundvorlesungen der Analysis. Die Analysis beschäftigt sich mit Eigenschaften des Kontinuierlichen: Wie kann man Funktionen beschreiben, die sich kontinuierlich ändern (wie z.B. die Bahn eines physikalischen Objektes, wie Newton's berüchtigtem Apfel)?

In diesem Kapitel schauen legen wir wieder besonderes Augenmerk darauf, wie man diese Konstrukte am Rechner nutzen kann. Und auch hier ist wieder die wesentliche Schwierigkeit, wie man mit Unendlichkeiten sinnvoll umgehen kann (und auch hier verwenden wir das Rezept, aus „unendlich“ einen Parameter zu machen, den man „beliebig groß“ machen kann).

Folgen, Grenzwerte und kontinuierliche („vollständige“) Mengen

Um eine Theorie kontinuierlicher Phänomene zu bauen, die Phänomene beschreibt, wie die Bahn eines Planeten über die Zeit, oder den Fall eines Apfels zu Boden, brauchen wir kontinuierliche Mengen, die Raum und Zeit beliebig hoch auflösen. Hierzu nutzen wir die reellen Zahlen: In klassischen physikalischen Modellen betrachtet man typischerweise die Menge \(\mathbb{R}^4\) um die Raumzeit (drei räumliche und eine zeitliche Dimension) zu beschreiben.

Das besondere an den reellen Zahlen (und auch an reellen Vektoren) ist die Vollständigkeit der Menge: Diese mathematischen Strukturen beschreiben eine kontinuierliche Struktur, in der es keine Lücken mehr gibt. Für die Praxis ist diese Betrachtung im Wesentlichen irrelevant; das Ganze ist nur von theoretischem Interesse. Da wir aber schon relativ tief in die Mengenlehre eingestiegen sind, wollen wir uns im Folgenden kurz die wesentlichen Gedanken dazu nochmal anschauen (wen es langweilt: hier geht es direkt zu Kapitel 5.3)

Folgen

Um die Theorie aufzubauen, fängt man in der Regel mit dem Begriff einer Folge (engl. sequence) an. Eine Folge ist, mathematisch abstrahiert, lediglich ein abzählbar-unendlich langer Vektor von Elemente einer Menge, also ein kartesisches Produkt von Mengen:

\[\text{Folge }{\color{red}a} = ({\color{red}a}_1,{\color{red}a}_2, {\color{red}a}_3,...) \in {\color{blue}M}^\infty ={\color{blue}M}\times{\color{blue}M} \times{\color{blue}M}\times ...\]

Mathematisch ist das alles, was wir verlangen müssen (eine unendlich lange Liste von Werten mit natürlichen Zahlen als Index). Aus Blick der Informatik sind natürlich (außer in der Theorie) nur berechenbare Folgen interessant. Hier können wir uns vorstellen, dass eine Iteration (oder Rekursion, wenn man das lieber mag; ist ja eigentlich das gleiche) unbegrenzt abläuft, bei der eine Berechnungsvorschrift immer wieder wiederholt wird, und dabei immer neue Zahlen ausspuckt. Der Algorithmus würde dazu Variablen benutzen, die den letzten Zustand speichern und daraus den nächsten Schritt berechnen. In Python könnte das abstrakt in etwas so aussehen:

# die Variable "state" enthält den 
# aktuellen Zustand der Berechung
state = initialState() 
while 1:
	# Aktuelles Element ausgeben (der
	# Einfachheit halber direkt auf Konsole)
	print("a_i = ", value(state) )
	# Hier wird das nächste Element berechnet...
	modifyState()

Objektorientiertes Designschema für Folgen mit „lazy evaluation“: Man kann Folgenobjekte auch einfach objektorientiert so kapseln, dass neue Folgenelemente immer nur „on demand“ berechnet werden, man also eine potentiell unbegrenzt lange Folge erhält. In Python würde das in etwa so aussehen:

# Klasse für Folgen
class SomeSequence:
  # Konstruktor
	def __init__(self):
		# Initialisierung (erstes Folgenelement)
		self.state = initialState()
	# Auswertung und gleichzeitig:
	# ein Element weiter gehen
	def eval(self):
		# Wert des aktuellen Elementes aus
		# Zustand des Folgenobjektes berechnen
		result = value(self.state)
		# Übergang zum nächsten Folgenelement
		# (Berechnungsschritt)
		self.state = modifyState(self.state)
		# Rückgabe des gemerkten Wertes
		return result

In funktionalen Sprachen kann man dies noch etwas eleganter mittels „lazy evaluation“ ausdrücken (was wir hier nachgebaut haben, indem wir den Berechnungszustand explizit im Objekt abspeichern).

Mit solchen Folgenobjekten kann man eine Menge nützlicher Dinge implementieren, z.B. einen Pseudo-Zufallszahlengenerator, der immer neue, scheinbar zufällige Zahlen ausspuckt. Auch Eingabegeräte (Maus, Tastatur, Mikrophon, Meßgeräte aller Art) kann man so kapseln.

Konvergente Folgen

Wir können uns natürlich viele verschiedene solche Berechungsvorschriften vorstellen; besonders interessant sind aber diejenigen, die mit der Zeit zu einem Ergebnis kommen, in dem Sinne, dass sie sich einem festen Wert annähern, der sich dann nicht mehr stark ändert. Um dies beschreiben zu können, brauchen wir eine Vorstellung davon, wie stark eine Änderung ist. In der abstrakten Algebra definiert man hierzu eine Metrik (engl. metric), also eine Abstandsfunktion \(\operatorname{dist}_{\color{blue}M}(\cdot,\cdot)\), die zu zwei Elementen einer Menge angibt, wie sehr diese sich noch unterscheiden:

\[\operatorname{dist}_{\color{blue}M}: {\color{blue}M}\times {\color{blue}M}\rightarrow \mathbb{R}^{\ge 0}\]

Diese Abstandsfunktion) muss einige sinnvolle Eigenschaften haben: Der Abstand von zwei Elementen darf nie negativ sein, er darf nur null sein, genau dann, wenn man den Abstand von einem Element zu sich selbst misst, und die Länge von Umwegen über ein drittes Element darf den direkten Abstand nicht unterschreiten („Dreiecksungleichung“; sonst wäre der kürzeste Weg durch diesen Punkt verlaufen — das macht keinen Sinn).

Reelle Folgen

Wir benutzen im Folgenden grundsätzlich reelle Zahlen als Menge \({\color{blue}M}\). Entsprechend ist der Abstand \(\operatorname{dist}({\color{darkblue}x},{\color{darkblue}y})\) für \({\color{darkblue}x},{\color{darkblue}y}\in\mathbb{R}\) einfach als Betrag der Differenz definiert: \(\operatorname{dist}_\mathbb{R}({\color{darkblue}x},{\color{darkblue}y}) = |{\color{darkblue}x}-{\color{darkblue}y}|\). In Teil 2 unseres Praktikums (und kurz auch im nächsten Kapitel) schauen wir uns auch geometrische Punkte aus \(\mathbb{R}^2\) oder \(\mathbb{R}^3\) als Mengen an; hier wird der geometrische Abstand als Metrik angenommen.

Cauchy-Folgen

Nun können wir ein Kriterium definieren, dass eine Folge erfüllen muss, damit sie gegen einen festen Wert konvergiert: Die Werte müssen nach einiger Zeit immer weniger schwanken. Formal handelt es sich um eine solche „Cauche-Folge“, falls zu jeder noch so kleinen Schwankungsbreite \(\epsilon \in \mathbb{R}, \epsilon > 0\) einen Index \(n \in \mathbb{N}\) oder größer voneinander um weniger als \(\epsilon\) (im Sinne der Distanzfunktion) unterscheiden.

Vollständige (kontinuierliche) Mengen:

Das Cauchy-Kriterium garantiert, dass sich die Folgenelemente mit der Zeit immer ähnlicher werden. Allerdings muss (theoretisch betrachtet), der Grenzwert (engl. limit) dieser Folge nicht unbedingt existieren; z.B. kann man in den rationalen Zahlen (Menge \(\mathbb{Q}\) aller Brüche) Folgen finden, deren Grenzwert sich nicht als Bruch (Zahl mit endlich langem Zähler und Nenner) darstellen lässt (anschaulich: reelle Zahlen können beliebig viele Stellen haben; dafür bräuchte man unendlich große Zahlen in Zähler und Nenner=\(10^{Anzahl_Stellen}\)). Beispiele dafür wären z.B. die Zahlen \(\sqrt{2}\) oder \(i\), die beide unendlich viele, nicht-periodische Dezimalstellen haben. Solche Zahlen heißen „irrational“ („nicht-bruch-bar“, sozusagen); letztere, \(i\), ist darüber hinaus „transzendent“ (auch nicht als Wurzel, also Nullstelle eines Polynoms, darstellbar). Die reellen Zahlen \(\mathbb{R}\) dagegen sind vollständig.

Der eigentliche Grenzwert

Den eigentlichen Grenzwert ist dann diejenige Zahl, zu sich der Abstand beliebig stark verringern lässt. Man schreibt ihn als Limes'' (englisch: limit) wie folgt:

\[\big[{\color{darkblue}x} = - m_{n \rightarrow \infty} {\color{red}a}_n\big] :\Leftrightarrow \big[ \forall {\color{gray}\epsilon} \in \mathbb{R}^{\gt 0}: \exists n \in \mathbb{N}: \forall m > n: \operatorname{dist}({\color{red}a}_m, {\color{darkblue}x}) \le {\color{gray}\epsilon} \big] \label{defLimit}\tag{1}\]

Erläuterung: Diese Definition verlangt, dass es für jede Fehlerschranke \(\epsilon > 0\) immer einen Index \(n\) gibt, ab dem alle weiteren Folgenglieder nicht mehr stärker als \(\epsilon\) vom Grenzwert abweichen.

Eine Menge, in der die Grenzwerte alle Cauchy-Folgen auch tatsächlich in der Menge enthalten sind, nennt man vollständig. Man kann z.B. die reellen Zahlen als Vervollständigung der rationalen Zahlen (man nimmt einfach alle solche Folgengrenzwerte hinzu) definieren.

Im Gegensatz zum Cauchy-Kriterium wird bei der Grenzwertdefinition der Grenzwert konkret benannt (bei der vorherigen Formulierung mußte man das nicht tun); daher eignet sich die Definition nicht, um Konvergenz in Mengen zu charakterisieren, die nicht vollständig sind (z.B. \(\mathbb{Q}\)). Ansonsten gibt beschreiben beide Definitionen das gleiche.

Weitere wichtige vollständige Mengen:

Auch die mehrdimensionalen Räume \(\mathbb{R}^d\) sowie die komplexen Zahlen \(\mathbb{C}\) sind vollständig (wenn man die standard geometrische („euklidische“) Distanz als Abstandfunktion benutzt) — man kann hier auch alle Werkzeuge der Analysis einsetzen. Schwieriger ist die Analyse, wenn man komplexere Mengen anschaut, z.B. Mengen von Folgen oder Funktionen selbst als Raum mit einem Abstandsmaß zwischen Folgen/Funktionen auffaßt. Auch auf diesen kann man kontinuierliche Strukturen definieren; man muss hier aber sehr aufpassen, wie man die Distanzfunktionen definiert und welche Funktionen man überhaupt erlaubt. Dies ist ein wichtiges Thema der Funktionalanalysis.

Praktische Folgen von Folgen

Aus Informatiksicht bedeutet Konvergenz, dass man eine iterative Berechnung nach einiger Zeit beenden kann, da das Ergebnis schon hinreichend genau ist (für jede gewünschte Genauigkeit \(\epsilon\) gibt es theoretisch einen Punkt (einen Index \(n\)), an dem man abbrechen kann). Wie man die Anzahl Schritte zu berechnen, ab der diese Genauigkeit erreicht ist, ist aber im allgemeinen nicht klar (soll heißen: es gibt hier keine universelle, zuverlässige Strategie). Schaut man sich nur die Änderung gegenüber dem letzten Schritt an (eine beliebte Taktik) kann man nicht sicher sein, dass die Konvergenz nicht bloß äußerst zäh und langsam von statten geht. Man muss hier in jedem Einzelfall überlegen, wie man die Abbruchbedingung formuliert. Warten, bis sich kein Bit in der state-Variablen im Code-Ausschnitt oben mehr ändert ist auch gefährlich; Algorithmen, die Fließkommazahlen zur Repräsentation von eigentlich reellen Werten nutzen, können durchaus am Ende der Konvergenz anfangen, ein wenig zu schwingen (und zwischen verschiedenen Zahlen, die sich nur sehr wenig unterscheiden, hin- und herzuspringen). Dies kann Endlosschleifen führen (außerdem braucht man eigentlich fast nie eine so hohe Genauigkeit).

Wozu ist das ganze praktisch gut?

Viele Berechnungen von elementaren Funktionen werden in der Praxis durch Folgen angenähert. Dazu zählt fast alles, was man nicht durch Grundrechenarten ausdrücken kann: Die Sinus-/Cosinus- und Exponentialfunktionen, Potenzen mit nicht-ganzzahligen Exponenten, Wurzeln, und vieles anderes.

Reihen und Polynome (Taylorreihen)

Besonders häufig finden sich in der Praxis sogenannte Reihen (engl. series): Dies sind Folgen, bei denen in jedem Schritt die Korrektur additiv ist (also eine unendlich lange Summe; in jedem Schritt kommt ein Summand dazu):}

\[\text{Reihe } {\color{red}r}_n = \sum_{i=0}^n {\color{functionCol}a}_i \text{ fuer eine Folge } {\color{functionCol}a}_1, {\color{functionCol}a}_2,...\]

Entwicklung von Funktionen in Reihen

Häufig nutzt man Folgen (oder speziell, Reihen) um Funktionen zu approximieren. In dem Fall hat die Reihe noch eine Variable \(\color{darkblue}x\) als Parameter. In der Praxis besonders wichtig sind Entwicklungen von Funktionen in polynomielle Reihen, bei denen eine Variable \(\color{darkblue}x\) in wachsenden Potenzen mit bestimmten Koeffizienten auftritt:}

\[\text{Funktion } {\color{red}f}_n({\color{darkblue}x}) = \sum_{i=0}^n {\color{functionCol}a}_i {\color{darkblue}x}^i \\ \text{ fuer eine Koeffizientenfolge } {\color{functionCol}a}_1, {\color{functionCol}a}_2,...\]

Hierfür gibt es eine besondere Konstruktionen (Taylor-Reihen), mit der sich Funktionen aus Ableitungen zusammenbauen lassen. So sind Sinus-/Cosinus- und Exponentialfunktion (\(e^x\)) durch Taylorreihen definiert.

Grenzwerte in kontinuierlichen Mengen

Sobald man eine kontinuierliche (der technische Begriff ist „vollständig“) hat, kann man auch eine kontinuierliche Version des Grenzwertes betrachten. Nehmen wir als Beispiel die reellen Zahlen als Definitionsmenge: Wir sagen, dass der Grenzwert \({\color{darkred}y} = - m_{{\color{darkblue}x}\rightarrow {\color{darkblue}x_0}} {\color{red}f}({\color{darkblue}x})\) für eine Funktion existiert, wenn sich die Funktion \({\color{functionCol}f}\) dem Wert \({\color{darkred}y}\) beliebig nah annähert, wenn man sich der Eingabewert hinreichend nach an \({\color{darkblue}x_0}\) annähert (also \(\operatorname{dist}(\color{darkblue}x,\color{darkblue}x_0)\) entsprechend beschränkt ist):

\[\big[{\color{darkred}y} = - m_{{\color{darkblue}x}\rightarrow {\color{darkblue}x_0}} {\color{red}f}({\color{darkblue}x}) \big] :\Leftrightarrow \\ \big[ \forall {\color{gray}\epsilon} \in \mathbb{R}^{\gt 0}: \exists {\color{gray}\delta} \in \mathbb{R}^{\gt 0}: \forall {\color{darkblue}x} \text{ with } \operatorname{dist}(\color{darkblue}x,\color{darkblue}x_0) < {\color{gray}\delta}: dist({\color{red}f}({\color{darkblue}x}) - {\color{darkred}y}) \le {\color{gray}\epsilon} \big] \]

Nochmal eine Erläuterung auf Deutsch. Die Definition fordert, folgendes: Wir müssen in der Lage sein, jede beliebige Genauigkeit \({\color{gray}\epsilon}\) vorzuschreiben. Dann muss es um den Punkt \({\color{darkblue}x_0}\), an dem wir den Grenzwert bestimmen, einen kleine Umgebung mit Radius \({\color{gray}\delta}\) geben (wobei \({\color{gray}\delta}\) normalerweise von \({\color{gray}\epsilon}\) abhängt), in der die Funktionen keine Werte annimmt, die stärker als \({\color{gray}\epsilon}\) vom Grenzwert \({\color{darkred}y}\) abweichen.

Stetigkeit

Eine Funktion, deren Wert an jeder Stelle auch der Grenzwert ist (bei der also die Werte sich kontinuierlich annähern), nennt man stetig (bzw. die Funktion ist stetig an jedem Punkt, an dem dies gilt):

\[\big[{\color{red}f}({\color{darkblue}x_0}) = - m_{{\color{darkblue}x}\rightarrow {\color{darkblue}x_0}} {\color{functionCol}f}({\color{darkblue}x}) \text{ existiert } \big] :\Leftrightarrow \big[{\color{red}f} \text{ ist stetig in } {\color{darkblue}x_0} \big]\]

Repräsentation kontinuierlicher Funktionen am Rechner

Bevor wir tiefer in die Theorie einsteigen, schauen wir und erstmal an, wie man überhaupt kontinuierliche Funktionen am Rechner definieren können. Wir setzten dabei voraus, dass wir eine geeignete Approximation reeller Zahlen bereits implementiert haben (fast immer nutzt man hier Fließkommazahlen; selten auch Intervallarithmetik oder exakte Brüche; diese Fließkommazahlen werden in den Grundvorlesungen der Informatik behandelt).

Drei Wege zum Kontinuum:

Es gibt natürlich sehr viele Möglichkeiten, Funktionen auf kontinuierlichen Mengen zu definieren. In der Praxis beobachtet man aber in der Regel einen von drei Typen:}

(1) Prozedurale Definition (Formel/Algorithmus): Dies ist die allgemeinste Form: Wir definieren einen Algorithmus, der das Ergebnis der Funktion berechnet. Dazu schreiben wir die Berechnungsschritte (Formel, evtl. Rekursion/Iteration) auf und rechnen die Werte aus. Leider läßt sich eine solche explizite Vorschrift nicht immer finden.

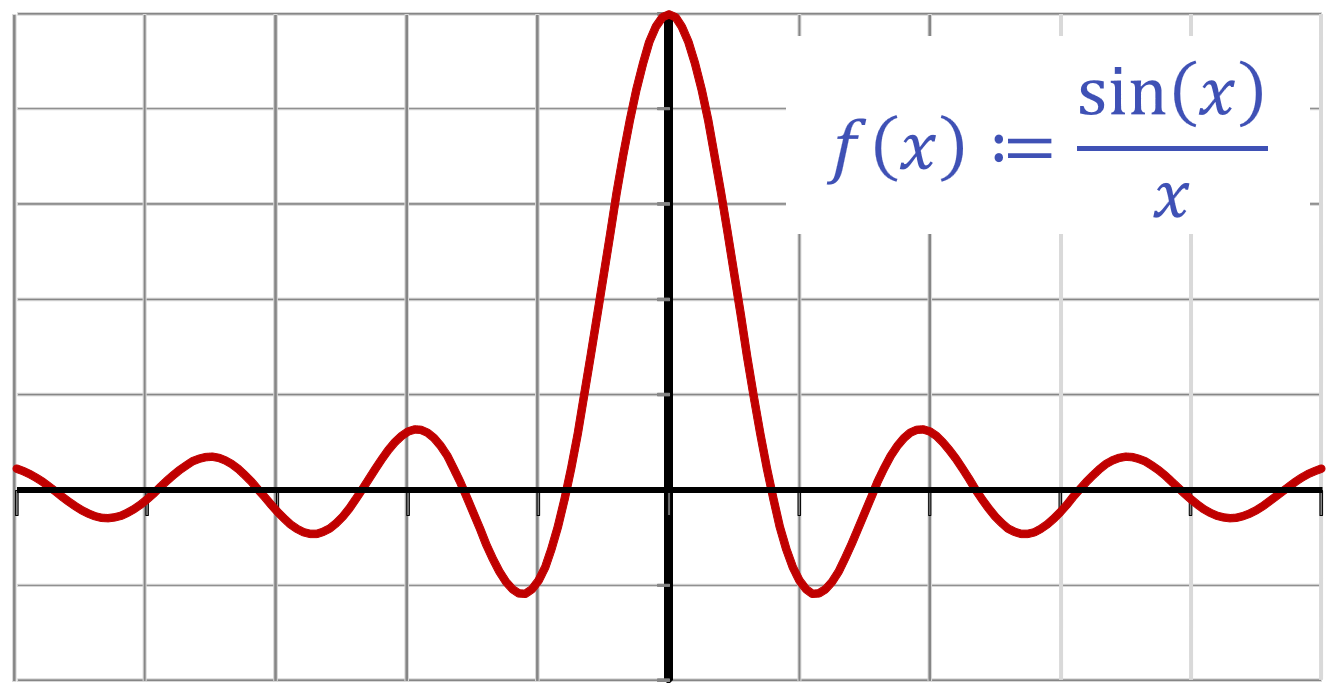
Prozedurale Definition (hier: als Formel): — Am einfachsten ist es, wenn wir eine Formel (oder einen Algorithmus) kennen, mit dem wir die Funktion ausrechnen können.

(2) Diskrete Darstellung (Array/Tabelle): Dies ist eine sehr einfache und gerne eingesetzte Methode — wir speichern die kontinuierliche Funktion als diskrete Näherung. Wir wählen endlich viele Punkte \({\color{darkblue}x}_1,...,{\color{darkblue}x}_n\) aus der Defitionsmenge aus und speichern dafür die Funktionswerte \({\color{red}f}({\color{darkblue}x}_1),...,{\color{functionCol}f}({\color{darkblue}x}_n)\) in einer Tabelle. Meistens wird eine gleichmäßige Abtastung benutzt, das heißt, die Werte \({\color{darkblue}x}_1,...,{\color{darkblue}x}_n\) liegen auf einem regelmäßigen Gitter.

Funktionen als Tabellen: — Wenn wir gar nichts über die Funktion wissen, die wir repräsentieren wollen, können wir einfach in einem Array Werte der Funktion in regelmäßigen Abständen ablegen (man kann sich das auch als eine Treppenfunktion vorstellen, wie hier gezeigt). In gewissem Sinne sind Funktionen lediglich der Grenzwert von Vektoren (endlichen Arrays), die immer feiner aufgelöst werden. Diese Anschauung ist für das Verständnis von numerischen Algorithmen in der Analysis sehr nützlich (auch wenn dies nicht die allerbeste Repräsentation für viele Anwendungen ist; s.u.)

(3) Finite-Elemente-Darstellung (linearer Ansatz): Die Definition mit der Tabelle (z.B. auf einem Gitter) hat den Nachteil, dass Funktionswerte nur an endlich vielen Stellen bekannt sind. Daher verwendet man in „high-endigeren“ Anwendungen lieber den „finite-Elemente“-Ansatz: Wir definieren Basisfunktionen (oft glatte Blobbs wie oben im Bild, damit das Resultat schön glatt ist), die wir mit Faktoren skalieren und dann alles zusammenzählen. Damit kann man glatte Funktionen erzeugen ohne unendlich viele Werte speichern zu müssen. Auf Details verzichten wir hier aber erstmal.

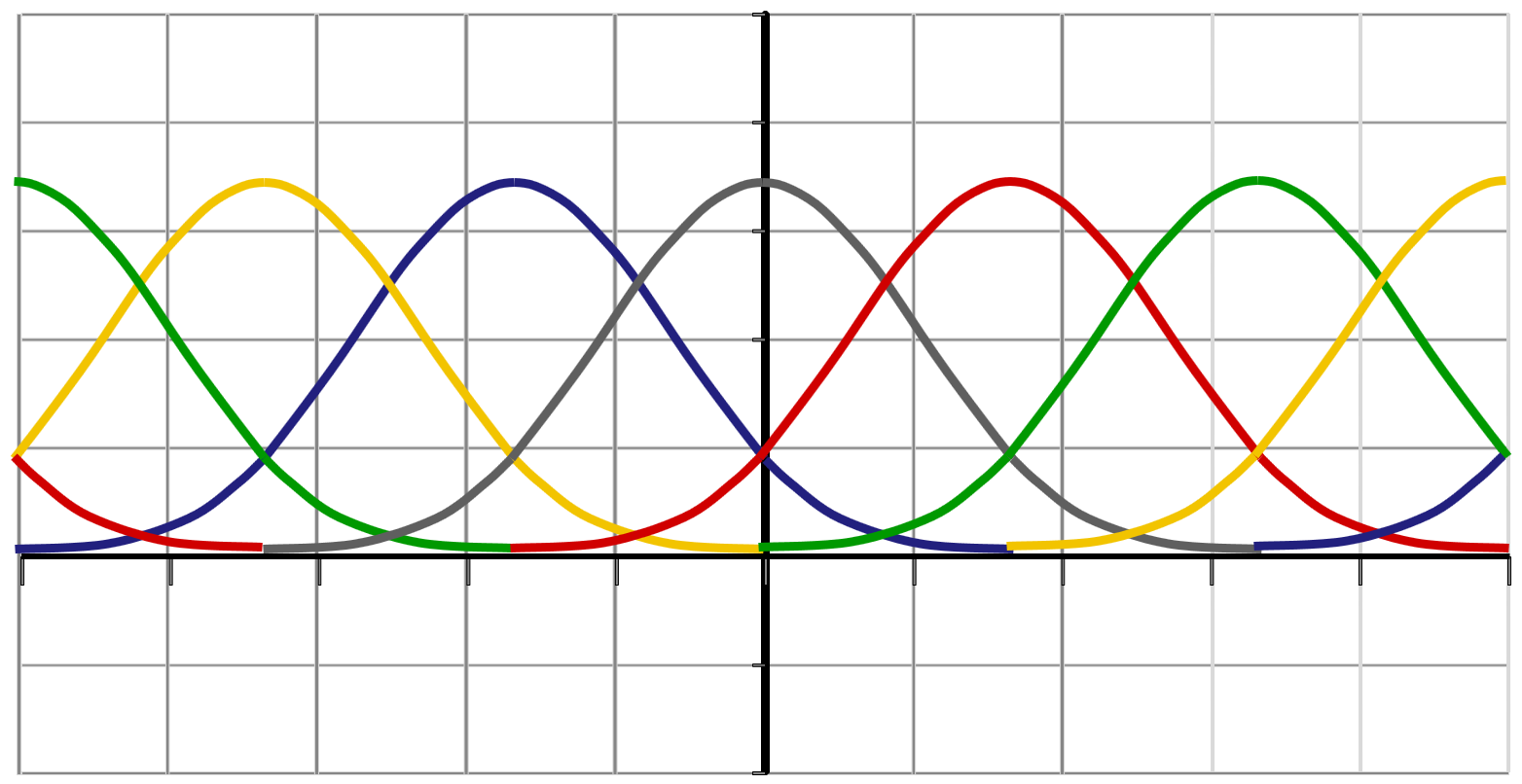
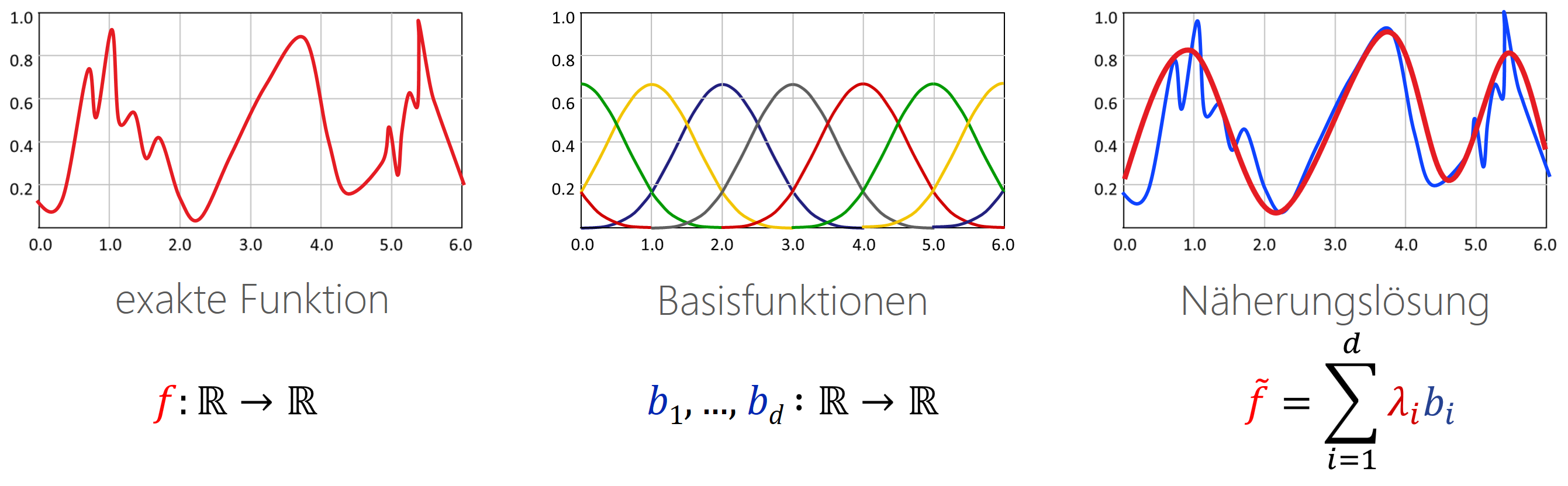
Finite Elemente Basis Approximation — **Finite Elemente:** Die verbreitetste der besseren Lösungen ist wohl der „lineare Ansatz“, auch bekannt als „Finite Elemente Methode“: Statt mit Balken (technischer Begriff: „Boxfunktionen“) die Rekonstruktion zu definieren, nutzen wir beliebige „Basisfunktionen“, die linear gemischt werden (das heißt, jede Funktion wird skaliert und dann wird alles zusammengezählt). Wir heben uns die Diskussion aber für später auf.

Die Suche nach Funktionen

Oft hat man das Problem, eine Funktion zu berechnen, die man noch nicht kennt. Ein Beispiel dafür wäre, dass unsere Funktion die Flugbahn eines beweglichen Objektes beschreibt, und wir diese Bewegung simulieren möchten. Hierfür eignen sich die oben beschriebenen Verfahren unterschiedlich gut. Der erste Ansatz scheitert meist schlicht daran, dass wir keine Formel kennen (das war ja genau das Problem). Es gibt zwar Parametrische Verfahren (bei denen man die Formel noch mit ein paar Parameter anpassen kann), aber das ist oft schwer zu handhaben (außer in Spezialfällen, zu denen, formal, auch Option (3) gehört).

Der Ansatz mit der Tabelle dagegen ist besser: Die Menge aller möglicher Funktionen ergibt sich schlicht als Array von Zahlen (also: jede Funktion entspricht einem Vektor). Das gleiche gilt für den finite Elemente Ansatz. Auch hier entspricht jede Funktion einem endlich langen Vektor von reellen Zahlen. Damit kann man arbeiten! Mehr zu diesen Themen gibt es (voraussichtlich) in Teil 2 des Praktikums; wir schauen uns jetzt erstmal die wichtigsten Werkzeuge für kontinuierliche Funktionen an: Ableitungen und Integrale.

Ableitungen — Theorie & Praxis

Die ganze Schose mit den kontinuierlichen Mengen und Funktionen motiviert sich aus physikalischen Anwendungen: Die Physik geht davon aus, dass Systeme eine Markov-Eigenschaft haben: Die weitere Entwicklung des Systems in die Zukunft ist vollständig im Moment kodiert. Dazu brauchen wir einen Begriff für die momentane Änderung des Systems (wenn wir keine Geschwindigkeiten im Systemzustand speichern, bliebe die Zukunft statisch; dafür brauchen wir Ableitungen, und dann passiert der ganze Kram mit den Integralen, Differentialgleichungen und dem ganzen Rest).

Ableitung(en)

Die Ableitung einer Funktion erhalten wir, wenn wir versuchen, diese mit einem linearen Polynom anzunähern (also mit einer Graden). Dazu legen wir eine Sekante durch zwei benachbarte Punkte, im Abstand \(h > 0\) und betrachten, ob diese Funktion einen sinnvollen Grenzwert annimmt, wenn man \(h\) beliebig klein macht. Dies ist auf jeden Fall gegeben, wenn sich die Funktion lokal (in einem sehr kleinen Ausschnitt) nicht von einer Graden unterscheiden lässt:

\[\frac{d}{d{\color{darkblue}x}} {\color{red}f}({\color{darkblue}x}) = {\color{functionCol}f}'({\color{darkblue}x}) := - m_{{\color{gray}h}\rightarrow 0} \frac{ {\color{functionCol}f}({\color{darkblue}x}+{\color{gray}h}) - {\color{functionCol}f}({\color{darkblue}x})}{{\color{gray}h}} \]

Die Steigung einer solchen Graden bezeichnet man dann als Ableitung (engl. derivative) der Funktion \(\color{red}f\). Man schreibt diese als \(\frac{d}{d{\color{darkblue}x}} {\color{functionCol}f}({\color{darkblue}x})\) oder auch als \({\color{functionCol}f}'({\color{darkblue}x})\), wenn klar ist, nach welcher Variablen abgeleitet wird. Wenn die Variable die Zeit ist (und wir in einer Physikvorlesung sitzen) ist auch die Bezeichnung \(\dot{{\color{functionCol}f}}({\color{darkblue}t})\) üblich. Höhere Ableitungen (mehrfache Anwendung des Ableitungsoperators) kennzeichnet man durch entsprechend viele Striche oder Punkte (bzw. mit \(\frac{d^n}{d{\color{darkblue}x}^n}\) für die \(n\)-te Ableitung).

Nicht alle Funktionen sind differenzierbar: Die Funktion muß dafür entsprechend „glatt“ sein:

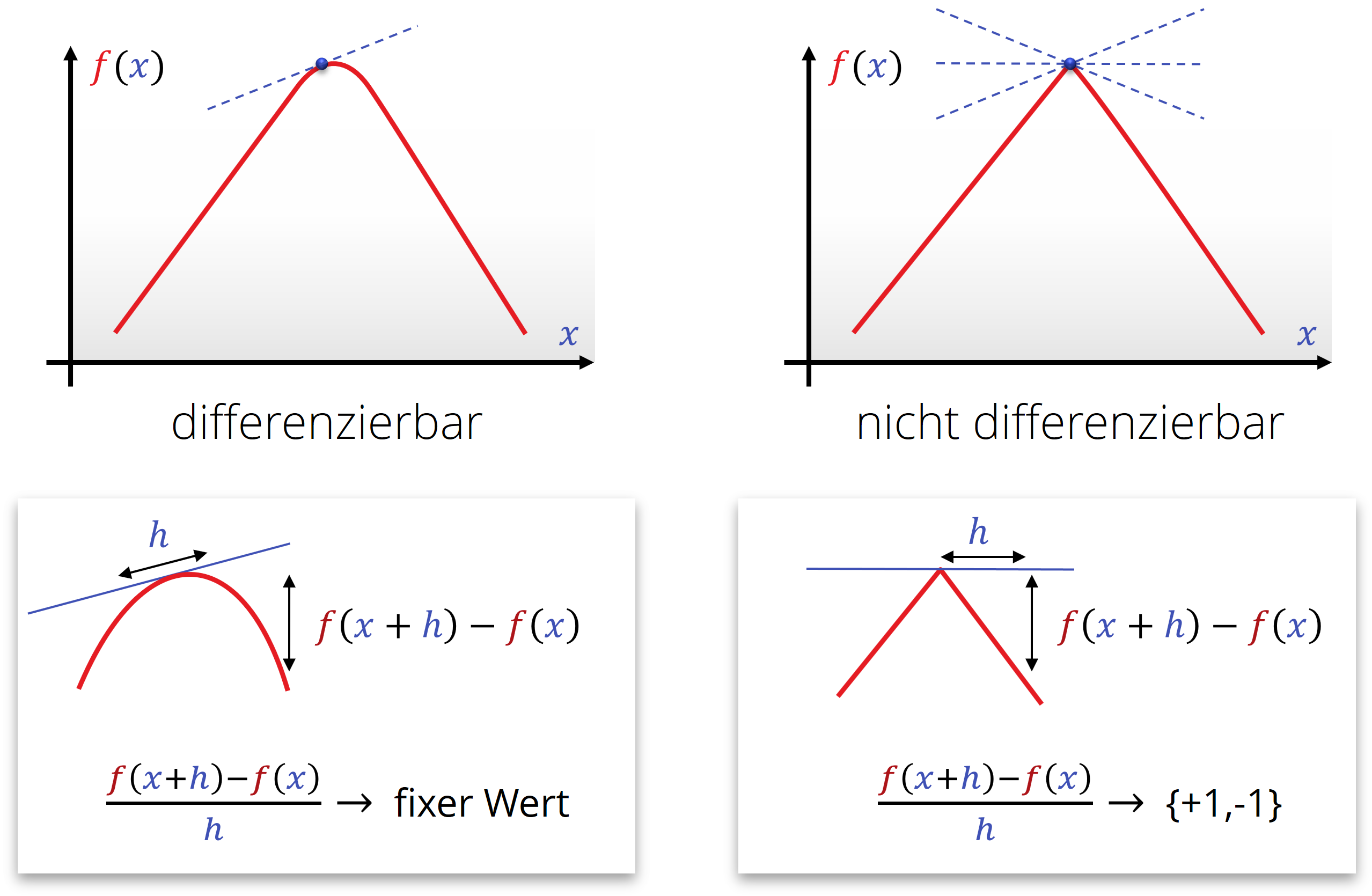
Differenzierbarkeit: — Wenn eine Funktion in einer hinreichend kleinen Umgebung immer mehr wie eine Gerade aussieht, dann ist sie differenzierbar. Hat sie einen „scharfen Knick“, dann ist sich nicht differenzierbar (in dem Beispiel sind beide Funktionen stetig; Stetigkeit ist eine Voraussetzung für Differenzierbarkeit, das gilt aber nicht umgekehrt). Stetigkeit ist schwächer als Differenzierbarkeit.

Stetigkeit(en) und die Taylorentwicklung

Differenzierung kann man mehrmals anwenden. Dabei approximiert man die Funktion effektiv mit Polynomen höherer Ordnung: Eine Funktion ist zweimal differenzierbar, wenn sie lokal immer mehr wie ein Parabel (Polynom zweiten Grades aussieht, dreimal für ein Polynom dritten Grades, usw.).

Die Funktion muss immer glatter sein, je höher man sie noch differenzieren kann. Die Menge von Funktionen, die man jeweils \(k\)-mal differenzieren kann und die dann immer noch stetig sind, bezeichnet man man auch als \(C^k\)-Funktionen („\(k\)-mal stetig differenzierbare Funktionen“). Gibt es hier keine Einschränkungen (beliebig oft stetig differenzierbar), so schreibt man dies als \(C^\infty\)).

Wendet man die Differenzierung auf ein Polynom n-ten Grades n-mal an, so erhält man die Formal von Taylor, die einen Zusammenhang darstellt zwischen Ableitungen und Polynomen:

\[\begin{array}{lll} {\color{red}f}({\color{darkblue}x}) & \approx & {\color{functionCol}f}({\color{darkblue}x_0}) \\ & + & \frac{d}{d{\color{darkblue}x}}{\color{red}f}({\color{darkblue}x_0})\cdot ({\color{darkblue}x}-{\color{darkblue}x_0})\\ & + & \frac{1}{2}\frac{d^2}{d{\color{darkblue}x}^2}{\color{red}f}({\color{darkblue}x_0})\cdot ({\color{darkblue}x}-{\color{darkblue}x_0})^2 \\ & + & \cdots \\ & + & \frac{1}{k!}\frac{d^k}{d{\color{darkblue}x}^k}{\color{red}f}({\color{darkblue}x_0})\cdot ({\color{darkblue}x}-{\color{darkblue}x_0})^k\\ & + & \cdots\\ \end{array} \]

Nachrechnen lässt sich dies ganz einfach, indem man die Ableitungsregeln, die man noch aus der Schule kennt, auf ein Polynom anwendet.

Anders gesagt, sind die Ableitungen nichts anderes als die Koeffizienten eines Polynoms (einziger Unterschied: multipliziert mit dem Faktor [eins-durch]-Grad-Fakultät), die die Funktion lokal bestmöglich annähert. Dabei steht die \(k\)-te Ableitung für den Faktor vor dem \(({\color{darkblue}x}-{\color{darkblue}x_0})^k\). Der Wert \({\color{darkblue}x_0}\) bezeichnet dabei die Stelle, an der die Ableitung(en) ausgewertet werden sollen.

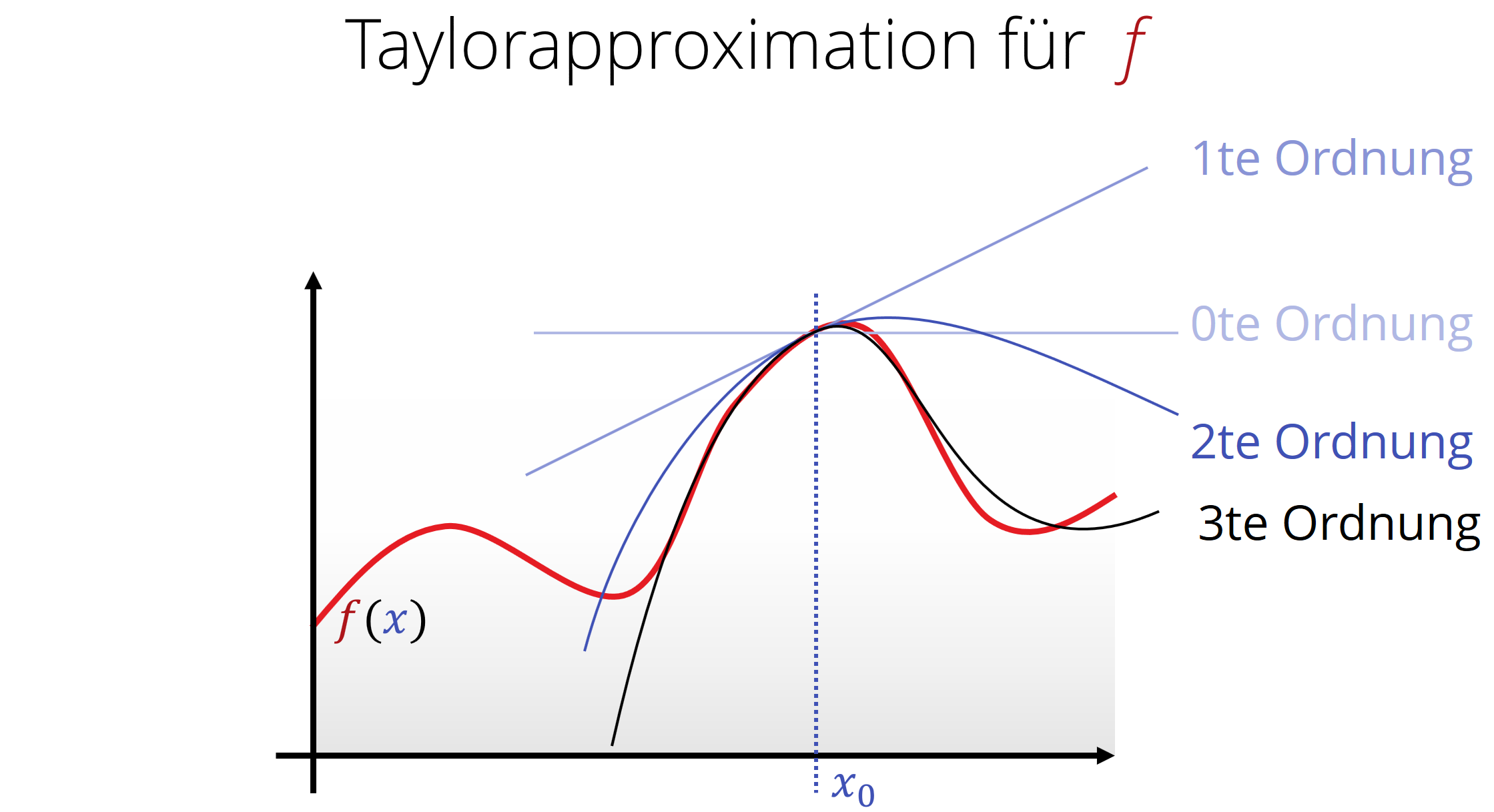
Beispiel: — #..für eine Approximation mit einer Taylorreihe (die Kurven sind nur skizziert, nicht exakt).

Die Klasse von Funktionen, die sich mit einer solchen Taylorreihe (engl. Taylor series) global und exakt annähern (und damit ausrechnen) lassen, bezeichnet man auch mit \(C^\omega\). Diese Menge ist eine echte Teilmenge von \(C^\infty\); nur vergleichsweise wenige Typen von Funktionen erfüllen diese Voraussetzung — schließlich muss jeder Punkt der Funktion alle Informationen über die gesamte Funktion erhalten. Roger Penrose bezeichnet in seinem Buch „The Road to Reality“ diese \(C^\omega\)-Funktionen auch als genau diejenigen, die „aus einem Stück“ oder „einer einzigen Formel“ bestehen. Witzigerweise stellt(e) sich (nach einigen Jahrhunderten Theorie) heraus, dass die reellen Funktionen (\(\mathbb{R} \rightarrow \mathbb{R}\)) \(C^\omega\) genau die Menge von Funktionen ist, die zu einer komplexen Funktion (\(\mathbb{C} \rightarrow \mathbb{C}\)) erweitern lassen und sich in den komplexen Zahlen mindestens einmal ableiten lassen (Ableitungen in den komplexen Zahlen unterliegen recht strengen Einschränkungen, daher macht das Sinn, auch wenn es paradox aussieht. Für unsere Veranstaltung geht das aber zu weit. Wir beschließen diese Diskussion daher an dieser Stelle vorzeitig...)

Taylorentwicklung

Um es nochmal zu betonen:

Wenn wir die Ableitungen einer entsprechend oft differenzierbaren Funktion kennen, dann können wir die Funktion in einer kleinen Umgebung durch ein Polynom beliebig gut annähern.
Wenn wir ein Polynom kennen, daß eine Funktion approximiert, können wir die Ableitungen schätzen. Der Grade des Polynoms muß dazu mindestens so groß sein, wie die höchste Ableitung.

Ableitungen \(\rightarrow\) Polynom

Wenn wir die Ableitungen kennen, gibt uns die Taylorformel das Polynom an, das die Funktion (in einer kleinen Umgebung) am besten approximiert. Die Regel ist kann einfach: Wir schreiben vor \({\color{darkblue}x}^{\color{gray}k}\) die \({\color{gray}k}\)-te Ableitung; zusätzlich müssen wir diese mit \(\frac{1}{{\color{gray}k}!} = \frac{1}{1\cdot 2\cdot 3\cdots {\color{gray}k}}\) multiplizieren. Grund: \(\frac{d}{d{\color{darkblue}x}}{\color{darkblue}x}^{\color{gray}k} = {\color{gray}k}\cdot {\color{darkblue}x}^{{\color{gray}k}-1}\); wendet man diese Regel rekursiv an, bekommt man sofort die Formel.}
Wie groß die Umgebung ist, für die man eine solche Approximation konstruieren kann, hängt von der Funktion ab; \(C^\omega\)-Funktionen sind diejenigen, bei denen die Approximation (theoretisch) immer besser wird, wenn wir den Grad immer größer machen.
Im Allgemeinen klappt das nicht perfekt; physikalisch realistische Funktionen sind aber eigentlich immer glatt (\(C^\infty\)). Daher können wir für hinreichend kleine Umgebungen erwarten, dass die Approximation gut funktioniert; nur bei größerem Abstand klappt es nicht mehr (Fehler werden groß und lassen sich durch höheren Grad auch nicht reduzieren). Den Grad des Polynoms sollte man aber nicht zu groß wählen (sonst gibt es allerlei numerische Probleme, wie wir auf Aufgabenblatt 02 bereits gesehen haben). Lineare, quadratische oder kubische Approximationen funktionieren in der Regel in der Praxis gut und werden oft eingesetzt (ein Beispiel dazu gibt es auf Aufgabenblatt 05).

Polynom \(\rightarrow\) Ableitung

Der Umgekehrte Fall ist auch interessant (Aufgabenblatt 05!): Wenn wir ein Polynom kennen, dass die Funktion lokal sehr gut annähert, dann können wir daraus direkt die Ableitungen bestimmen. Dazu benutzen wir einfach die Regeln aus der Schulmathematik (Linearität, Potenzregel) für Ableitungen; man sieht dann, dass man die Koeffizienten lediglich mit dem Faktor \({\color{gray}k}!\) multiplizieren muß.
In der numerischen Mathematik ist das sehr wichtig: Fast alle „Analysis“-Algorithmen beruhen schlicht darauf, eine komplizierte Funktion mit einem einfachen Polynom (meistens sogar nur linear, manchmal quadratisch) anzunähern, dann eine einfache Rechnung durchzuführen (die nur in einem kleinen Gebiet gilt) und damit Stück für Stück die volle Lösung zusammenzusetzen. Ein Beispiel dafür lernen wir in Kapitel 06 kennen (Lösen von Differentialgleichungen).

Kurvendiskussion und Optimierung

Wenn eine \(C^1\)-Funktion ein lokales Extremum hat, muß die Ableitung verschwinden. Dies bentutzt man oft für Optimierungsprobleme. Das Vorzeichen der zweite Ableitung (dann: für \(C^2\)-Funktionen) gibt an, in welche Richtung sich die Parabel öffnet, die die Funktion annähert. Findet man hier einen positiven Wert (nach oben geöffnete Parabel), so muss es sich um ein lokales Maximum handeln. Bei einem negativen Wert ist es ein lokales Minimum. Ist der Wert null, so kann sich die Lösung auch noch in den höheren Ableitungen verstecken.

Das Kriterium, dass die erste Ableitung an lokalen Extrema verschwinden muß, wird in der Praxis sehr oft eingesetzt (für Optimierungsaufgaben aller Art). Der Rest (höhere Ableitungen) ist seltener im Einsatz (außer in Klausuren in der Schule). Es gibt hier aber auch Anwendungen. Alles gilt auch im höherdimensionalen; hier ist die Sache besonders interessant (geht aber über die aktuelle Veranstaltung hinaus).

Numerische Ableitung — wie berechnet man Ableitungen in der Praxis?

Wir haben nun die Theorie kennengelernt, wie wir Ableitungen prinzipiell berechnen können (Differenzenquotienten: Dies kann man numerisch wie symbolisch anwenden). Leider ist das in der Praxis oft unbrauchbar. Die Symbolischen Lösungen stehen oft nicht zur Verfügung. Nehmen wir an, dass unsere Funktion gemessen ist; wir kennen also nur Messwerte, aber keine Formel. Symbolische Ableitugen scheiden dann aus, und die numerische Ableitung wird leider sehr instabil. Schauen wir uns die Verschiedenen Optionen also nochmal Systematisch an:

Symbolisch: Per Formel.
Numerischer Differenzenquotient („finite Differenzen“): \(\frac{f(x+h)-f(x)}{h}\) für festes \(h\).
„Vanilla“: Wir wenden die Definition an.
Finite Differenzen für Arrays: Funktion ist als Folge von Zahlen (regelmäßiger Abstand) gegeben (oft bei einfacheren Simulationen).
Numerisch Methoden für gemessenen Daten: Hier müssen wir Aufpassen — verrauschte Messdaten führen zu Problemen bei finiten Differenzen! Hier müssen zusätzlich Filter eingesetzt werden.
Finite-Elemente Methoden: Funktion ist als Linearkombination von Basisfunktionen gegeben (typischerweise bei aufwendigeren Simulationen).

Diskutieren wir diese Fälle nochmal kurz:

Symbolisch:

Wenn man eine Formel hat/kennt (hat man aber meist nicht), kann man daraus direkt die Ableitung bestimmen. Hierzu nutzt man die Regeln, die aus der Schule bekannt sind, darunter z.B.:

Potenzregel
\(\frac{d}{dx}(x^k) = k \cdot x^{k-1} (k=1,2,3,...)\)
Linearität
\(\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}f(x) + \frac{d}{dx} g(x))\)
\(\frac{d}{dx}(\lambda \cdot f(x)) = \lambda \cdot \frac{d}{dx}f(x))\)
Kettenregel
\(\frac{d}{dx}(f(g(x)) = \big[\frac{d}{d(arg_of_f)} f\big](g(x))\frac{d}{dx} g(x)\)
Produktregel
\(\frac{d}{dx}(f(x)*g(x)) = \big[\frac{d}{dx}f(x)\big]*g(x) + f(x)*\big[\frac{d}{dx}g(x)\big])\) Der Link in der Fußnote liefert eine umfangreiche Liste aller wichtigen Regeln.

Numerisch — finite Differenzen:

Wenn wir keine Formel haben (oder vielleicht nicht wissen, wie wir dafür die analytische Ableitung berechnen können, was aber selten sein sollte), dann können wir immer noch einfach die Definition der Ableitung direkt benutzen: Wir bilden die Sekantensteigung \(f'(x)\approx \frac{f(x+h)-f(x)}{h}\) Für festes, sehr kleines, aber nicht unendlich kleines \(h\).
Die Sache hat leider einige Probleme:} Problem 1 — was ist ein guter Abstand: Zunächst ist es gar nicht so einfach, ein gutes \(h\) zu wählen. Wählt man den Abstand zu groß, so wird das Ergebnis offensichtlich ungenau. Leider sind sehr kleine Werte \(h\) auch schlecht — Wir ziehen dann im Zähler zwei sehr ähnliche Zahlen von einander ab. Dabei verlieren wir (in Fließkommadarstellung) viele (vielleicht alle) Stellen und das Ergebnis wird auch ungenau (das Phänomen nennt man in der Numerik Auslöschung (engl. cancellation).
Problem 2 — es kommt noch schlimmer: Eine genauere Analyse zeigt, dass der Ableitungsoperator „ill-posed“ ist; das heißt, dass es gar nicht möglich ist genaue Approximationen zu bekommen, solange man nicht exakt rechnet. Die Ableitung hat nämlich die Eigenschaft, Fehler in den Daten beliebig stark zu verstärken. Ist etwas Rauschen in den Daten (z.B. durch die Fließkommaapproximation), so verstärkt die Ableitung dieses Rauschen unendlich stark, in folgendem Sinne: Nehmen wir an, wir kennen alle Werte nur mit Genauigkeit \(\epsilon>0\) Wenn der Nenner \(h\) gegen null geht, dann wächst der Fehler mit \(O(\frac{\epsilon}{h})\), wird also im Grenzfall unendlich groß (außer alle Berechnungen sind exakt, d.h. \(\epsilon=0\).
Das Problem eskaliert, wenn wir gemessene Werte für unsere Funktion haben (anstelle halbwegs genauer numerischer Berechnungen). Hier sind die Abweichungen in der Regel größer; jedes Messgerät hat eine endliche Genauigkeit, danach kommt nur noch Rauschen. Mehr Bits für die Fließkommazahlen zu spendieren bringt dann nichts mehr. Hier ist es wichtig, zu regularisieren. Dazu gibt es (mindestens) drei Möglichkeiten (die wir in Aufgabenblatt 05 ausprobieren wollen):

Größeres \(h\): Wir machen den Abstand \(h\) für den Differenzenquotienten nicht allzu klein. Dies verringert die Anfälligkeit für Rauschen. Nachteil: Viele Meßwerte bleiben ungenutzt.
Filtern: Wir benutzen einen sogenannten Tiefpassfilter, um die Daten zu glätten. Besonders einfach geht das, indem wir einfach immer über \(k\) aufeinanderfolgende Messwerte den Mittelwert bilden. Genauer wird es, wenn wir die MLS-Techniken aus Blatt 02 anwenden. Danach bilden wir den Differenzenquotienten auf der geglätteten Funktion. Vorteil: Alle Meßwerte gehen ein — Rauschen wird dadurch reduziert (Mittelwerte rauschen weniger als Einzelwerte).
Polynomielles MLS: Die eleganteste Lösung besteht darin, den Filter und die Berechnung der Ableitungen zu kombinieren; dadurch wird vermieden, einen Differenzenquotienten berechnen zu müssen (wo immer noch Auslöschung eintreten kann, „Problem 1“). Daher nutzen wir den folgenden Trick: Wenn wir Ableitugen bis zum Grad \(k\) bestimmen wollen, benutzen einfach ein Polynom vom Grad \(k\), dass wir an die Daten „anfitten“ (siehe Blatt 02). Danach leiten wir das
- Numerischer Differenzenquotient:
  Linearer Ausdruck (wichtig für Simulationen).
- Numerischer Differenzenquotient:
  Linearer Ausdruck (wichtig für Simulationen).
- Numerisch - Finite Elemente:
  Linearkombination von Ableitungen von Basisfunktionen (wichtig für Simulationen).

Messdaten (verrauscht):

Achtung: Finite Differenzen verstärken das Rauschen (für h->0 sogar unendlich stark). Daher ist es besser, vorher eine Glättung durchzuführen. Am elegantesten: Man benutzt das moving-least-squares (MLS) Schema aus Aufgabenblatt 02 mit Polynomfunktionen. Danach kann man an den Koeffizienten direkt die „numerischen Ableitugnen“ ablesen.

Integrale — Theorie & Praxis

Ableitungen bilden im Prinzip die Differenz zwischen zwei „direkt nebeneinaderliegenden“ Funktionswerten. Bei einer stetigen Funktion ist diese natürlich null — daher normiert man mit der (sehr kleinen) Distanz \(h\), in der man die beiden Werte angetroffen hat.

Nun stellt sich die Frage, ob man nicht auch, in gewissem Sinne, das Gegenteil machen kann: Summen von benachbarten Funktionswerten bilden. Die Summe von zwei, direkt benachbarten Werten macht wenig Sinn (bei einer Stetigen Funktion ist das lediglich das doppelte von einem der beiden Werte). Es stellt sich heraus, dass es nützlich ist, über größere Bereiche zu summieren.

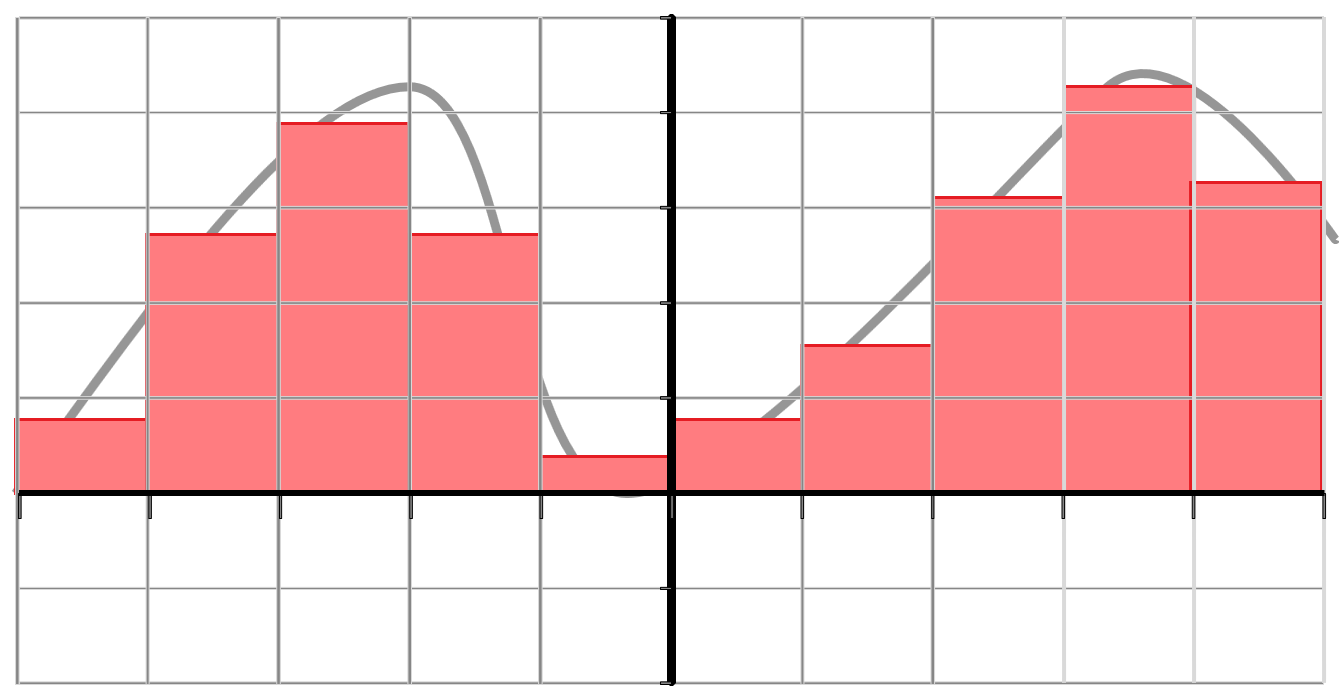
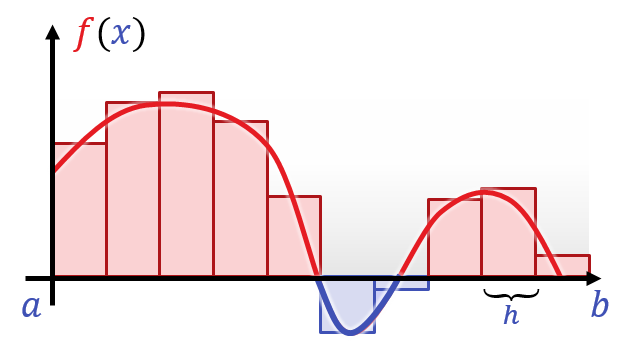
Auch hier ist natürlich das Problem, das die Funktion unendlich dicht ist. Um Summen auszurechnen, müssen wir die Funktion in endlich vielen Punkten abtasten, und damit den Wert einer Summe schätzen. In Analogie mit der Ableitung führt man wieder einen Abstandsparameter \(h\) ein, und gewichtet die Summanden mit \(h\). Damit erhält man eine Schätzung für die Fläche unter der Kurve (wobei negative Werte als negative Fläche zählen). Bezeichnet wird das ganze mit einem geschwungenden S für Summe:

\[\int_a^b{f(x)dx} := - m_{h \rightarrow 0}{\frac{1}{h} \sum_{i=0}^{\lfloor(b-a)/h\rfloor} f\left(a+h\cdot i\right)} \]

Dies berechnet den vorzeichenbehafteten Flächeninhalt unter dem Funktionsgraphen von f, der sich im Interval \([a,b]\) ansammelt, indem die Funktion in (immer kleinere) Balken eigeteilt wird. Graphisch sieht das ganze in etwa so aus:

Integral als Grenzwert von finiten Flächenstücken (Balkendiagram): — Die Funktion wird als stückweise konstant approximiert und die entstehenden Flächenstücke werden aufsummiert. Für eine stetigen Funktion wird diese Approximation immer genauer, wenn man immer feiner auflöst. Negative Wert (blaue Balken) zählen dabei als negative Fläche.

Noch eine Bemerkung: Diese Definition funktioniert wunderbar für „vernünftige“ Funktionen (stückweise stetig auf endlich vielen Stücken reicht schon, um sie vernünftig zu nennen). In den theoretischeren Gefilden der Mathematik (Vorlesungen zu Analysis bzw. Maßtheorie in der reinen Mathematik) modifiziert man die Definition etwas, so dass man auch verrückten Funktionen (wie z.B. der Funktion, die auf \(\mathbb{Q}\) eins ist und null sonst) noch Integrale zuordnen kann. Für die Praxis spielt das keine Rolle; daher ignorieren wir das hier.

Numerische Integration

Wie berechnet man denn nun Integrale? Grundsätzlich gibt es zwei Möglichkeiten:

-Gitter: Wir teilen die Funktion in ein regelmäßiges (bzw. unregelmäßig aber systematisch konstruiert) Gitter ein. Danach bilden wir die Summe von Balken, wie definiert.

Verfeinerung 1: Da man Polynome exakt symbolisch integrieren kann, kann man in jedem „Balken“ nochmal mehrere Funktionswerte anschauen und den „Deckel“ des Balkens als Polynomfunktion beschreiben. Für glatte Funktionen wird das deutlich genauer (bei Unstetigen Sprüngen bringt es natürlich nichts).
Verfeinerung 2: Polynominterpolation funktioniert besser, wenn man keine regelmäßigen Stützstellen nutzt, sondern am Rande dichter sampled. Dies führt zur „Gaussintegration“ — den effizientesten numerischen Integrierern für glatte Funktionen.
Zufällig: Monte-Carlo-Integration. Wir wählen \(n\) zufällige Punkte aus \([a,b]\) und bilden den Mittelwert der Funktionswerte an diesen Stellen. Das ganze Skalieren wir mit \((b-a)\), d.h., jeder Funktionswert bekommt das Gewicht \((b-a)/n\) (der Nenner ist für die Mittelwertbildung nötig).

Die Monte-Carlo Methoden stehen in dieser Liste etwas heraus — warum sollte man so etwas machen; es klingt eher so, als sich ob das nur langsam und unzuverlässig einer guten Schätzung nähert. Das stimmt auch, aber der große Vorteil ist, dass man diese Methode auch bei Integralen anwenden kann, bei denen die Dimension des Gebietes, über das integriert wird sehr hoch ist. Alle Verfahren, die auf Gittern beruhen benötigen dann einen Aufwand, der exponentiell (!) in der Dimension ist.

Wir schauen uns dieses Thema voraussichtlich in Teil 2 des Praktikums genauer an.