Algebra und algebraische Strukturen - Die Sache mit den Formeln

In diesem Kapitel kombinieren wir Mengen und Funktionen zu konkreten „Datentypen“. Zunächst definieren wir geeignete Operationen und führen Berechnungen durch, indem wir diese hierarchisch Schachteln (Kapitel 4.1). Danach (Kapitel 4.2) werdem wir von den konkreten Operationen abstrahieren, um Aussagen über ganze Klassen von ähnlichen Modellen zu machen. In der Mathematik führt dies zur abstrakten Algebra (engl. abstract Algebra), in der Klassen von Modellen abstrakt über Axiome konstruiert werden (ohne konkrete Umsetzungen/Implementationen zu betrachten). In der Informatik findet sich eine direkte Entsprechung in polymorphen Datenstrukturen (templates, Vererbung, traits, type-classes, etc.).

Algebra

Wenn wir uns mit Mathematik beschäftigen, verbringen wir einen großen Teil der Arbeit damit, formale Ausdrücke (Formeln) zu manipulieren (um Strukturen zu erkennen, Beweise zu führen, Rechnungen zu vereinfachen, Probleme zu lösen). In diesem Abschnitt möchten wir uns anschauen, wie man diese Objekte mit Mitteln der Informatik (am Rechner bzw. in einer Programmiersprache) repräsentieren kann. Dadurch wird hoffentlich klarer, was bei algebraischen Manipulationen, Berechnungen und Beweisen eigentlich vor sich geht.


Algebraische Ausdrücke

Ein algebraischer Ausdruck ist eine Rechenvorschrift, die typischerweise als Text kodiert aufgeschrieben wird, die aber eigentlich eine hierarchische Schachtelung von Funktionen und Variablen kodiert. Schauen wir uns dazu ein einfaches Beispiel an. Im folgenden seien \({\color{inputCol}x},{\color{inputCol}y} \in \mathbb{R}\) reelle Variablen. Damit bilden wir den Ausdruck: \[{\color{constInputCol}3} \cdot {\color{inputCol}x} + \frac{{\color{constInputCol}4} \cdot {\color{inputCol}y}}{{\color{constInputCol}5}}\]


Dieser Ausdruck entspricht einem Baum, in dem die inneren Knoten Funktionen sind und die Blattknoten Konstanten oder Variablen:


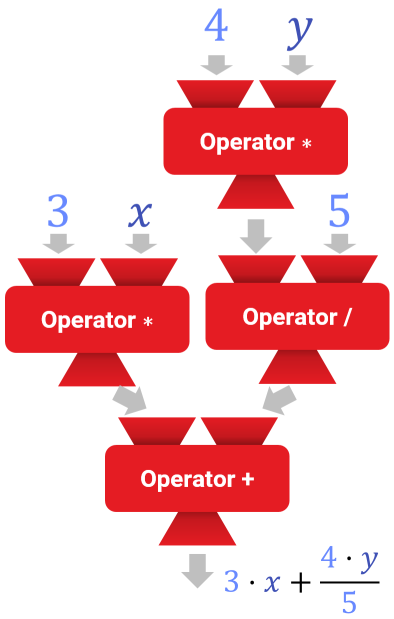
Operator als Baum Operator als Baum Operator als Baum Operator als Baum

(a) Funktionen als Rechenmaschinen, die Ergebnisse weitergeben

Operator als Baum Operator als Baum Operator als Baum Operator als Baum

(b) Darstellung als Graph/Baum. Die „Ein/Ausgabe-Pins kodieren den erwarteten/gelieferten Typ.

Algebraische Ausdrücke sind Bäume: Ein algebraischer Ausdruck kodiert eine Hierarchie (einen Baum) von geschachtelten Funktionen. Präzendenzregeln (Punkt-vor-Strichrechnung, etc.) und ggF. Klammern vermeiden dabei Mehrdeutigkeiten.

Allgemeine Typen
Das Prinzip kann nicht nur auf Ausdrücke (arithmetische Formeln) oder rekursive Berechnungsvorschriften (darin enthalten: ) angewendet werden sondern auch auf boolesche Ausdrücke (wahr/falsch). Damit lassen sich Aussagen in arithmetischer Form formulieren. Typische Operatoren sind logische Operatoren wie und/oder/negation und Schlußfolgerungen wie Implikation „\(\Rightarrow\)“ und Äquivalenz „\(\Leftrightarrow\)“. Beispiel:


\[\big[{\color{inputCol}n} \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}1} \big] \Rightarrow \big[({\color{inputCol}n}+{\color{constInputCol}1}) \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}0}\big]\]


Parameterübergabe
Das Binden von Parametern an Werte erledigt man, auch ganz analog zum Programmieren, durch die Definition einer benannten Funktion. Beispiel:


\[{\color{functionCol}aussage}: \mathbb{Z} \rightarrow \{wahr, falsch\},\\ {\color{functionCol}aussage}({\color{inputCol}n}) = \Big( \big[{\color{inputCol}n} \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}1} \big] \Rightarrow \big[({\color{inputCol}n}+{\color{constInputCol}1}) \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}0}\big]\Big)\]


Rekursion
Wie in Kapitel 3.5.1 bereits geschildert, können Funktionen auch rekursiv verwendet werden. Dazu ist selbstverständlich nötig, wie auch bei rekursiven Algorithmen in der Information, dass die Rekursion immer zu einem Abbruch kommt (oder zumindest eine Konvergenz eintritt, so dass man die Berechnung nach endlich vielen Schritten mit hinreichender Genauigkeit abbrechen kann; siehe unten). Oft erfolgt der Rekursionsabbruch mit einem Fallunterscheidungsoperator (ganz ähnlich wie bei rekursiven Algorithmen). Zeichnet man solche rekursiven Ausdrücke wie zuvor, so erhält dann einen zyklischen Graphen. Bei der Auswertung ändern sich aber die Parameter, was die Anzahl der Zyklen begrenzt. Der Fallunterscheidungsoperator wäre hierbei auch nur ein weiterer Typ von Knoten im Graphen.


Iteration
Man kann in mathematischer Notation auch direkt Schleifen definieren. Dazu gibt man (mindestens) eine Menge an und (mindestens) eine Funktion, die für alle Elemente der Menge ausgewertet und verknüpft werden soll. Beispiele wären:


Es gibt natürlich noch viele andere solche Konstrukte (man kann eigentlich jeden n-ären Operator so als „Iteration“ schreiben).


Unendliche Iteration bzw. Rekursion
Anders als in der Programmierung in der Informatik können mathematische Rekursionen (und Iterationen) auch unendlich lange laufen. Zum Beispiel wäre der folgende Ausdruck problemlos zulässig:


\[\forall {\color{inputCol}n} \in \mathbb{N} : \Big( \big[{\color{inputCol}n} \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}1} \big] \Rightarrow \big[({\color{inputCol}n}+{\color{constInputCol}1}) \operatorname{mod} {\color{constInputCol}2} = {\color{constInputCol}0}\big]\Big)\]


(Dieser Ausdruck hat den konstanten Wert „wahr“. Solche booleschen Ausdrücke nennt man auch mathematische Sätze.)


Bei booleschen Ausdrücken ist die Semantik unproblematisch — man muß nur ein Beispiel dafür oder dagegen finden, welches das Ergebnis bestimmt. Unendliche arithmetische Operationen erfordern etwas mehr Aufwand; sie sind Gegenstand des Gebietes der Analysis.


Abzählbarer Fall: Hier wird zunächst ein Grenzwertbegriff definiert und dann das Ergebnis einer unendlichen Summe as der Wert definiert, an den sich endliche, aber immer länger laufende Summe immer mehr annähern. Kontinuierliche (überabzählbarer) Fall: Um eine Summe über eine kontinuierliche Menge zu bilden (z.B. die reellen oder die komplexen Zahlen, oder eine Teilmenge davon), definiert man Integrale. Auch hier ist ein geeigneter Grenzwertbegriff der wesentliche Trick, mit dem man die Unendlichkeit modelliert. Im Unterschied zum diskreten (abzählbaren) Fall muß man aber der Menge, über die integriert wird, ein Maß zuordnen, damit die dicht-an-dicht liegenden Punkt nicht unvermeidlich zu unendlich großen Ergebnissen führen (hier nimmt man normalerweise den Flächeninhalt; ein einzelner Punkt hätte damit Maß 0 und Teilmengen erhalten ihren Flächeninhalt als Maß). Mehr dazu später.


Noch eine Bemerkung: Produkte über kontinuierliche Mengen werden nicht definiert; hier kann man aber (zumindest für strikt positive Werte) z.B. die Summe der Logarithmen der Funktionen (und danach die Exponentialfunktion), was den gewünschten Effekt hat, ohne dass wir ein neues Konzept definieren müssen.

Mathematische Notation, Datenstrukturen und Parsing

Mathematische Ausdrücke schreibt (zeichnet) man fast nie als Baum, sondern eher als linearisierte Folge von Symbolen. Auf Papier findet man hier etwas mehr Geometrie; wenn wir es in den Rechner bringen wollen, nutzen wir (wenn man keine aufwendige Mustererkennung machen will) eigentlich immer Zeichenketten (Strings).


Das Problem, was sich dort stellt, ist die Rekonstruktion einer hierarchischen Darstellung (Baum) aus der linearisierten Darstellung. Dieses Problem ist auch als Parsing (engl.) bekannt. Die Grundidee ist einfach; die Details leider recht komplex.


Grundidee: Jeder Baustein wird in eine hinreichend markante Abfolge von Zeichen umgewandelt Dazu werden die Daten jedes Knotens des Baumes als eine zusammenhängende Zeichenkette dargestellt. Ein Teil davon beschreibt die geschachtelten Unterknoten, ein anderer Teil die Informationen über den Knoten selbst. Um ein eindeutiges Parsing zu ermöglichen, müssen die Teile aus der Zeichenkette eindeutig identifiziert werden können (die Struktur des Baumes und alle Daten in den Knoten).


Die Details: ...kann man unterschiedlich schwierig gestalten. Das Gebiet wird in der theoretischen Informatik als Theorie „kontextfreier Sprachen“ (anderer Ausdruck für Linearisierungen von Bäumen geschachtelter Bausteine) behandelt. Die vielen Subtilen Details gehen über diesen Kurs weit hinaus. Nur ein kurzer Hinweis: Das Parsingproblem ist dann sehr einfach, wenn die Grenzen der Bausteine und die Schachtelung eindeutig markiert ist (z.B. über eine volle Klammerung und fixe Reihenfolgen von Parametern, wie in der Notation der Programmiersprache LISP). Je mehr Kontextinformation zur Auflösung von Mehrdeutigkeiten (bez. Schachtelung bzw. Grenzen der Bausteine) nötig wird, desto aufwendiger wird das Parsing.


Einen einfachen Parsingalgorithmus (für einfache Sprachen von Ausdrücken) schauen wir uns auf dem Aufgabenblatt 04 an.

Algebraische Umformungen

Umformungen


Für unsere mathematischen Typen (die wir im nächsten Abschnitt 4.2 noch genauer unter die Lupe nehmen) kennen wir Rechenregeln. Dies können entweder Eigenschaften sein, die wir für konkrete Typen bewiesen haben, oder abstrakte Axiome, die wir für unsere Typen vorausgesetzt haben (dies wird in Abschnitt 4.2 im Detail beleuchtet).
Wir können nun solche Regeln auf unsere Ausdrücke/Formeln anwenden. Jede mögliche Anwendung liefert uns einen modifizierten Ausdruck (als Datenstruktur betrachtet: Wir verändern den Operatorenbaum mit jeder Anwendung einer Regel). Das heißt, algebraische Umformungen sind nichts weiter als Transformationen eines Baumes (Graphen bei Rekursion) von Ausdrücken. Welche Transformationen erlaubt sind, hängt von den Regeln ab, die wir kennen. Die Regeln sind für verschiedene Typen definiert; es kann also sein, dass wir im selben Baum je nach Knoten verschiedene Regeln anwenden müssen/dürfen.

Sätze


Zur Erinnerung: Sätze sind auch nur Ausdrücke (Bäume/Graphen von Operationen), die insgesamt einen Boolschen Wert ergeben. Dieser sollte „wahr“ sein (damit der Satz stimmt).

Beweise


Beweise sind auch lediglich wahre boolesche Ausdrücke, die eine Kette von Implikationen von einer Teilmenge der Axiome hin zu einem bestimmten Satz (auch einem booleschen Ausdruck) aufbauen. Wir konstruieren einen Beweis, indem wir mit Axiomen (bzw. bekannten Rechenregeln) starten und danach Schritt-für-Schritt gültige Axiome/Rechenregeln anwenden (Achtung: Hier brauchen wir fast immer nicht nur die Regeln für unser(e) Zahlensystem(e) sondern auch die Axiome für die Aussagenlogik und die Mengenlehre). Betreibt man dies lange genug (in die richtige Rechnung) erhält man eine Folge von wahren Implikationen die mit als wahr vorausgesetzten Axiomen beginnt und mit der zu beweisenden Aussage endet.

Automatisches Beweisen mit dem Rechner


Wir können versuchen, automatisch Beweise zu führen. Das Problem ist unberechenbar in dem Sinne, dass es keinen Algorithmus gibt, der für jede Aussage (in einem hinreichend komplexen Axiomensystem; z.B. einem solchen, dass die natürlichen Zahlen umfasst) automatisch Beweise führt. Warum? Naja, wir wissen aus Kapitel 3, dass es nichtmals unbedingt immer solche Beweise geben muss (auch zu entscheiden, ob ein Beweis existiert, ist im allgemeinen leider unberechenbar).
Das Problem ist aber einseitig lösbar (der technische Begriff ist „rekursiv aufzählbar“): Falls ein Beweis existiert, können wir ihn immer algorithmisch finden. Die Idee ist sehr einfach: Wir schreiben einen Algorithmus, der alle Beweise, die möglich sind, aufzählt und abbricht, wenn der richtige gefunden wurde (also am Ende unserer Implikationskette die zu beweisende Aussage steht). Falls der Beweis nicht existiert, läuft der Algorithmus ewig. Sollte die Aussage beweisbar falsch sein, klappt es trotzdem, indem wir Aussage und ihr Gegenteil parallel zu beweisen versuchen.

Wie setzt man das praktisch um? Wir können einen rekursiven Branch-and-Bound-artigen Algorithmus verwenden. Wichtig ist hier die „richtige Intuition“ — wir wollen nur Zweige in unserem Suchbaum verfolgen, die wahrscheinlich zu einer Lösung führen werden. Im allgemeinen ist der Aufwand utopisch hoch (exponentiell in der Anzahl notwendiger Beweisschritte), aber inzwischen gibt es recht starke Heuristiken sowie Algorithmen für spezielle, effizienter lösbare Spezialfälle, so dass automatisches Beweisen zu einem gewissen Grade in der Praxis nutzbar wird (natürlich immer mit dem Risko, dass der Rechner nach einiger Zeit aufgeben muss, weil keine Lösung gefunden werden konnte).

Nochmal zusammengefasst...

Algebraische Ausdrücke sind lediglich Bäume von Operatoren und Variablen/Konstanten. Die Variablen können gebunden sein, entweder durch Knoten im Baum, die man in der Informatik „Iteratoren“ oder „Schleifen“ nennen würde (Summen-/Produktzeichen, logische Quantoren, Mengenoperationen, etc.) oder durch Parameter einer Funktion (explizit, durch Definition einer Funktion, oder implizit, durch den Kontext, indem die Ausdrücke verwendet werden).


Ausdrücke können allerlei Typen haben (Mengen, Werte, Funktionen sowie alle Möglichen Kombinationen davon). Im Operatorenbaum muss sichergestellt sein, dass alle Typen zusammenpassen. In der Informatik bekommt man dazu Compilerfehler; beim Schreiben auf Papier merkt man aber oft nicht sofort, dass da etwas nicht stimmt (eine häufige Fehlerquelle — man macht sich oft nicht klar, welche Typsemantik die Objekte haben, die man da so verknüpft...).


Was aber genau ist ein Typ? Das haben wir bisher nur unzureichend behandelt. Mehr dazu im nächsten Abschnitt!


Axiomatische Algebra, abstrakte Datentypen und Polymorphie

Wie wir gerade gesehen haben, haben alle mathematischen Objekte wohldefinierte Typen (genau wie Datenobjekte in jeder höheren Programmiersprache). Bislang haben wir Typen in der Mathematik als Mengen aufgefasst (und für die Verwendung in der Informatik schlicht die möglichen Elemente in solchen Mengen [typischerweise binär] kodiert). Das ist aber nur die Hälfte der Geschichte: Zu den Typen gehören auch noch passende Funktionen, die mit den „Daten“ arbeiten. Wir kennen das in der Informatik: In objektorientierten Programmiersprachen stellen wir immer Memberfunktionen bereit, die fest mit bestimmten Typen verbunden sind. Auch prozedurale und funktionale Sprachen verknüpfen in der Regel Funktionen mit Typen, für die diese Funktionen aufgerufen werden können. In allen Fällen kann dies (wie in Kapitel 2 besprochen) explizit erfolgen (statische Typisierung: der Programmierer gibt dies im Code vor) oder implizit (dynamische Typisierung: Prüfung zur Laufzeit; oder auch: statische Typisierung mit Typinferenz — der Compiler schließt indirekt auf die richtigen Typen).


Wir gehen nun in zwei Schritten vor: Zunächst können wir konkrete Typen bilden; danach bauen wir generische Mechanismen indem wir generische Typen einführen.

Konkrete Typen

Um einen konkreten mathematischen Typ zu definieren (wie wir ihn zuvor bereits schon die ganze Zeit implizit verwendet haben), müssen wir zwei Dinge tun: Bei einem konkreten Typ würden wir die Funktionen in der Regel auch explizit definieren (also z.B. für die natürlichen Zahlen die Rechenvorschriften als Algorithmen definieren, wie wir sie in der Grundschule lernen).
Sätze/Axiome: Im weiteren kann man die Algorithmen genauer studieren und eine Reihe von Rechenregeln feststellen; diese kann man dann benutzen, um Eigenschaften von definierten Konstrukten zu analysieren. Eine Menge von Eigenschaften, aus der sich alle anderen ableiten lassen, nenn man auch ein Axiomensystem.
Das Vorgehen soweit entspricht in etwa dem, was man in der Informatik als „abstrakten Datentyp“ kennt (sozusagen die Aussagenlogische Variante der Idee; statt Algorithmen geht es um Mengen und Zuordnungen zwischen Mengen). Nun sollte klar sein, was als nächstes kommt: Wir brauchen viele verschiedene Typen, und diese Typen werden bestimmte Eigenschaften (aber nicht alle) gemeinsam haben. Um nicht immer wieder von Null anfangen zu müssen (also alle Algorithmen und Beweise von Grund auf neu aufzuschreiben), sollten wir polymorphen Code benutzen (statt für nur für Berechnungen nun (auch) für Beweise). In Programmiersprachen gibt es dafür einen ganzen Zoo an Tools (parametrische Polymorphie, wie Generics/Templates, dynamische Polymorphie, wie Vererbung/Subklassen, usw.). In der mathematischen Analyse können wir es uns einfacher machen (da es nicht effizient auf einem Prozessor ablaufen muss): Wir schreiben einfach fest, welche Eigneschaften ein Typ haben muss, damit er für eine Rechnung geeignet ist.

Abstrakte Typen und abstrakte Algebra

In der modernen Algebra arbeitet man vorwiegend mit abstrakten Typen. Hierzu werden die Eigenschaften aufgezählt, die ein Typ mindestens erfüllen muss; dann werden Beweise nur aufgrund dieser Eigenschaften geführt. Gelegentlich werden auch Algorithmen entwickelt (und in der Regel analysiert; z.B. mit Korrektheits- / Laufzeitbeweisen); auch hier ist oft eine generische Formulierung möglich. Kombinationen von Eigenschaften, die oft zusammen verwendet werden, erhalten einen besonderen Namen. Grundsätzlich ist man darauf bedacht, mit minimalen Mengen von Eigenschaften zu arbeiten, aus denen sich alle weiteren beweisen lassen (also mit Axiomen (engl. Axioms).
Beispiel für eine abstrakte Algebraische Struktur: Gruppen
Schauen wir uns ein Beispiel an. Eine wichtige Struktur, die immer wieder auftaucht, ist die algebraische Gruppe (engl. Group. Gruppen bestehen aus einer Menge und einer Operation, für die einige Axiome gelten: Die algebraische Struktur \(({\color{inputSetCol**G},\circ})\) ist eine Gruppe, genau dann wenn:

Die Struktur der Gruppe findet sich in vielen konkreten Typen wieder. Hier sind einige Beispiele: Alle diese Beispiele, außer dem letzten, sind kommutativ. Wir sollten auch noch kurz darauf hinweisen, dass alle diese vorgenannten Beispiele noch andere Operationen definieren; wir schauen uns hier also nur einen Teilaspekt einer größeren Struktur an.
Interessanterweise sind die Gruppen \((\mathbb{R},+)\) und \((\mathbb{R^{\neq 0}}, \cdot)\) isomorph. Das heißt, es gibt eine Bijektion (in diesem Fall \(\ln\) bzw. \(\exp\)) zwischen den Mengen, die so geartet ist, dass es egal ist, ob man Operationen in der einen oder anderen Darstellung (vor oder nach der Abbildung) ausführt (\(\ln(a\cdot b) = a+b\)). Gleiches gilt für \((\mathbb{C},+)\) und \((\mathbb{R^2},+)\) (hier ist die Isomorphie trivial; wir fassen den Imaginärteil einfach als y-Koordinate auf; siehe Aufgabenblatt 03). Die beiden Äquivalenzklassen (1D reelle Zahlen und 2D reelle Zahlen) unterscheiden sich allerdings strukturell erheblich. Dennoch können wir Beweise und Algorithmen generisch für alle solche Strukturen führen, und generische Algorithmen formulieren. Schauen wir uns zwei Beispiele an: Ein generischer („polymorpher“) Beweis:
Nehmen wir an, dass \(G\) eine Gruppe ist, und \(a,b,c \in G\). Außerdem bezeichnen wir das neutrale Element mit \(n\). Dann gilt: \[a \circ b \circ c = n \\ \Rightarrow b \circ c = a^{-1}\]
Beweis: Wir multiplizieren beide Seiten der Gleichung von rechts (wichtig, da wir keine Kommutativität verlangt haben!) mit \(a^{-1}\).
Ein generischer („polymorpher“) Algorithmus:
Nehmen wir an, dass \(G\) eine Gruppe ist, und \(a \in G\). Wir wollen nun die „von \(a\) erzeugte Untergruppe \(\langle a \rangle \subseteq G\) berechnen:
Initialisiere Ausgabemenge \(M = \emptyset \)
Setze
\(b = a\)
Solange \(b \notin M\)
\(\qquad M = M \cup b\)
\(\qquad b = a \circ b\)
Rückgabe \(M\)
Für \(G=(\mathbb{Z} \operatorname{mod} 4, +)\) und \(a=2\) liefert der Algorithmus \(\{0,2\}\). Für \(G=(\mathbb{Z} \operatorname{mod} 8, +)\) und \(a=2\) liefert der Algorithmus \(\{0,2,4,6\}\). Für \(G=(\mathbb{R}, +)\) und \(a=2\) terminiert der Algorithmus nicht (offensichtlich).

Abstrakte Typen in Programmiersprachen

Die definition abstrakter Datentypen und deren polymorphe Benutzung ist ein zentrales Problem beim Entwurf von Programmiersprachen. Hierzu wurden eine ganze Reihe von Konzepten entwickelt:
Einfachvererbung (z.B. JAVA)
Bei der Vererbung werden abstrakte Typen durch Oberklassen repräsentiert. Bei klassischen Sprachen wie JAVA (auch: Object-Pascal) kann man Typen nur verfeinern. Das heißt, man kann nur speziellere Typen von allgemeineren ableiten. Mathematisch entspricht das dem, dass wir zusätzliche Axiome hinzufügen (beim Programmieren sind dies oft implizite Annahmen darüber, wie die Memberfunktionen eines Typs arbeiten).
Mehrfachvererbung/Interfaces (z.B. C++ und Python; letzteres auch in JAVA)
Bei der Mehrfachvererbung kann man Funktionen und Eigenschaften definieren, und diese danach relativ frei vermischen. Damit sind flexiblere Konstruktionen möglich. Leider kann es zu unschönen Mehrdeutigkeiten („Diamond-Star-Problem“) kommen, wenn nicht nur die Annahmen, sondern auch noch der Code und die Datenstrukturen vererbt werden, die diese Operationen implementieren. Konservative Sprachen wie JAVA verbieten dies daher (weitgehend; neuere Versionen erlauben die Vererbung von Code aber nicht von Daten). C++ und Python sind da liberaler; man muss aber sehr aufpassen, wenn man dieses Feature praktisch benutzt. Die Analogie zu den mathematischen Strukturen ist lediglich, dass Eigenschaften auf Untertypen übergehen, und man Mengen von Eigenschaften kombinieren kann. Das ist unproblematisch (da die Programmiersprache dies in der Regel gar nicht repräsentiert).
Generische Typen/Templates (vor allem C++, m.E. in JAVA, unnötig in Python)
Bei generischen Typen (auch bekannt als „parametrische Polymorphie“) enthält der Code noch Typparameter, die bei der Nutzung des Types ausgefüllt werden können und müssen. In C++ wird hierzu „Ducktyping“ verwendet: Der Compiler setzt den Typ einfach copy-paste in den Quelltext ein und übersetzt diesen erneut, wenn ein generischer Typ verwendet wird.
Polymorphie durch dynamische Typisierung (Python, m.E. auch JAVA, C++):
Python hingegen ist vollständig dynamisch typisiert: Man kann als Parameter für Funktionen immer beliebige Objekte übergeben. Fehler werden erst festgestellt, falls zur Laufzeit eine Operation auf einem solchen Objekt aufgerufen werden sollte, die undefiniert oder aus anderen Gründen nicht erlaubt ist. Die Bindung von Funktionen (Operationen) an Typen (Mengen) erfolgt durch dynamische Bindung (jedes Objekt hat eine Kennzeichnung, in der der Typ steht, über die eine Tabelle an dieses Objekt gekoppelter Methoden nachgeschlagen werden kann).
Ein weiterer Aspekt ist die Prüfung der Verwendung von Typen auf Konsistenz. Hierzu gibt es auch mehrere Ansätze:
Untypisierte Sprachen (z.B. Maschinensprache, m.E. C/C++/Pascal): Die Vogel-Strauss-Strategie. Der Programmierer darf keine Fehler machen.

Dynamische Typisierung (z.B. Python, m.E. C++/JAVA): Erst wenn eine Funktion ausgeführt wird, wird überprüft, ob die Datentypen für die Operation geeignet sind. Auch weitere Eigenschaften und Annahmen können dynamisch geprüft werden („Assertions“). Dies muß man in den meisten Programmiersprachen explizit implementieren; Fehler werden nicht allgemein erkannt, sondern nur im konkreten Fall (keine Garantien für allgemeine Konsistenz). Manche Programmiersparchen (z.B. D/ADA/Rust) stellen spezielle Mechanismen bereit, um zusätzlich Annahmen dynamisch zu Prüfen (z.B. via Pre-/Postconditions von Funktionen).


Statische Typisierung (z.B. Haskell/ML, m.E. C++/Pascal/ADA/JAVA): Dies ist der Fall, der uns hier besonders interessiert (den Rest hatten wir schon in Kapitel 2 angeschaut): Ein statisches Typsystem kann man auch so verstehen, dass für jeden Datentyp Annahmen (Axiome oder auch oft, der Einfachheit halber, übervollständige Systeme von Annahmen) definiert sind, die immer wahr sein müssen. Der Compiler in einer statisch typisierten Sprache beweist nun zur Laufzeit, dass alle Annahmen immer, in jedem denkbaren Programmablauf erfüllt sein werden. Nochmal: Eine statisch typisierte Sprache wie Haskell, JAVA oder C++ (nicht Python) beweist beim Compilieren, dass bestimmte Annahmen immer erfüllt sein werden.


Das klingt zu gut um wahr zu sein; ist leider auch zu gut (trotzdem wahr). Wie wir bereits aus Kapitel 3 wissen, ist die Aufgabe, allgemeine Eigenschaften von Programmen zu beweisen, leider nicht berechenbar. Daher muß man die Dinge, die Menge der Eigenschaften, die man hier testen kann, leider stark einschränken. In JAVA (und auch in C/C++/Pascal, wenn man riskante low-level-features nicht nutzt) beweist der Compiler lediglich, dass ein Zugriff auf ein Datenelement immer den erwarteten Typ vorfindet, falls er jemals ausgeführt werden sollte (in C/C++/Pascal sind die Garantien schwächer, wenn man dynamisch alloziierten Speicher nutzt, da Zeiger auch in unalloziierten Speicher zeigen können; in JAVA werden dann dynamische Fehler „NullPointerException“ erzeugt). Komplexere Eigenschaften kann man leider nicht definieren. Zum Beispiel wäre es praktisch, vorab zu beweisen, dass eine doppelt-verkettete Liste immer korrekt verzeigert ist; solche Eigenschaften kann man aber in keiner dieser Sprachen vom Compiler überprüfen lassen.


In dieser Hinsicht moderne Sprachen (wie z.B. Haskell oder Rust) bieten etwas stärkere Typsysteme; die Grenzen sind leider auch hier recht eng. Man kann zeigen, dass die automatische Lösung des Problems (Berechnung eines zur formalen Problemspezifikation passenden Algorithmus durch den Compiler) und das Beweisen allgemeiner Eigenschaften gleich schwere unlösbare Probleme sind.