Grundlagen II: Funktionen, Berechenbarkeit und emergente Komplexität
Funktionen
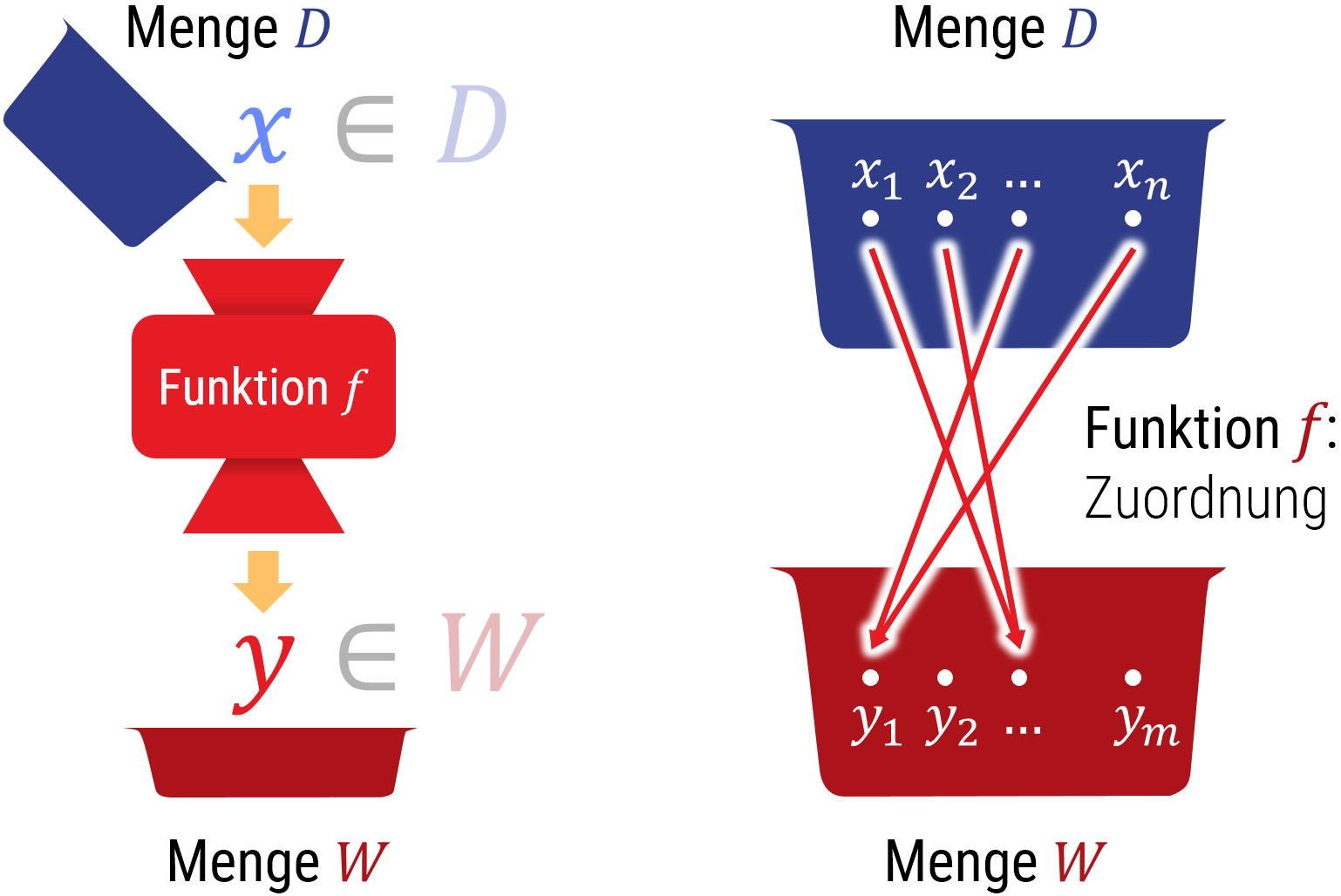



Linkes Bild: Man kann sich Funktionen als abstrakte Maschinen vorstellen, die Informationen verarbeiten (aus der Eingabe eine Ausgabe berechnen). Wir werden aber später sehen, daß man mit der Sprache der Mathematik Funktionen definieren kann, für die es keine realen Maschinen gibt, die diese tatsächlich berechnen würden. Dies kann aber nur dann auftreten, wenn die Definitionsmenge unendlich groß ist.
Rechtes Bild: Daher ist es sinnvoll, eine mathematische Funktion, anders als eine Funktion in typischen Programmiersprachen, als rein abstrakte Zuordnung zu verstehen (ohne darüber nachzudenken, ob und wie diese berechnet werden könnte).
Funktionen in der Mathematik
Der zweite Baustein für mathematische Modelle ist der Begriff der Funktion (engl. function). Funktionen ordnen den Elementen einer Menge jeweils ein Element einer anderen Menge zu. Die Eingabemenge heißt dabei Definitionsmenge (engl. domain (of definition)) und die Ausgabemenge heißt Zielmenge (auch Wertemenge / Wertebereich, engl. codomain, auch target set). Die Notation hierfür (sozusagen die Deklaration einer Funktion in der Sprache der Mathematik) sieht folgendermaßen aus: \[ {\color{red}f}: {\color{darkblue}D} \rightarrow {\color{darkred}W} \] Die Zuordnung eines Elementes \(\color{darkblue}x \in {\color{darkred}W}\) zum Funktionswert \({\color{darkred}f}\left({\color{darkblue}x}\right)\) kann man auch wie folgt festhalten: \[ {\color{darkblue}x} \mapsto {\color{darkred}f}\left({\color{darkblue}x}\right) \] Der Pfeil mit dem Querstrich am Anfang deutet darauf hin, daß hier die Zuordnung von Elementen beschreiben wird. Läßt man diesen weg, so definiert man die „Signatur“ einer Funktion, d.h., man beschreibt, von welchen Mengen in welche andere abgebildet wird.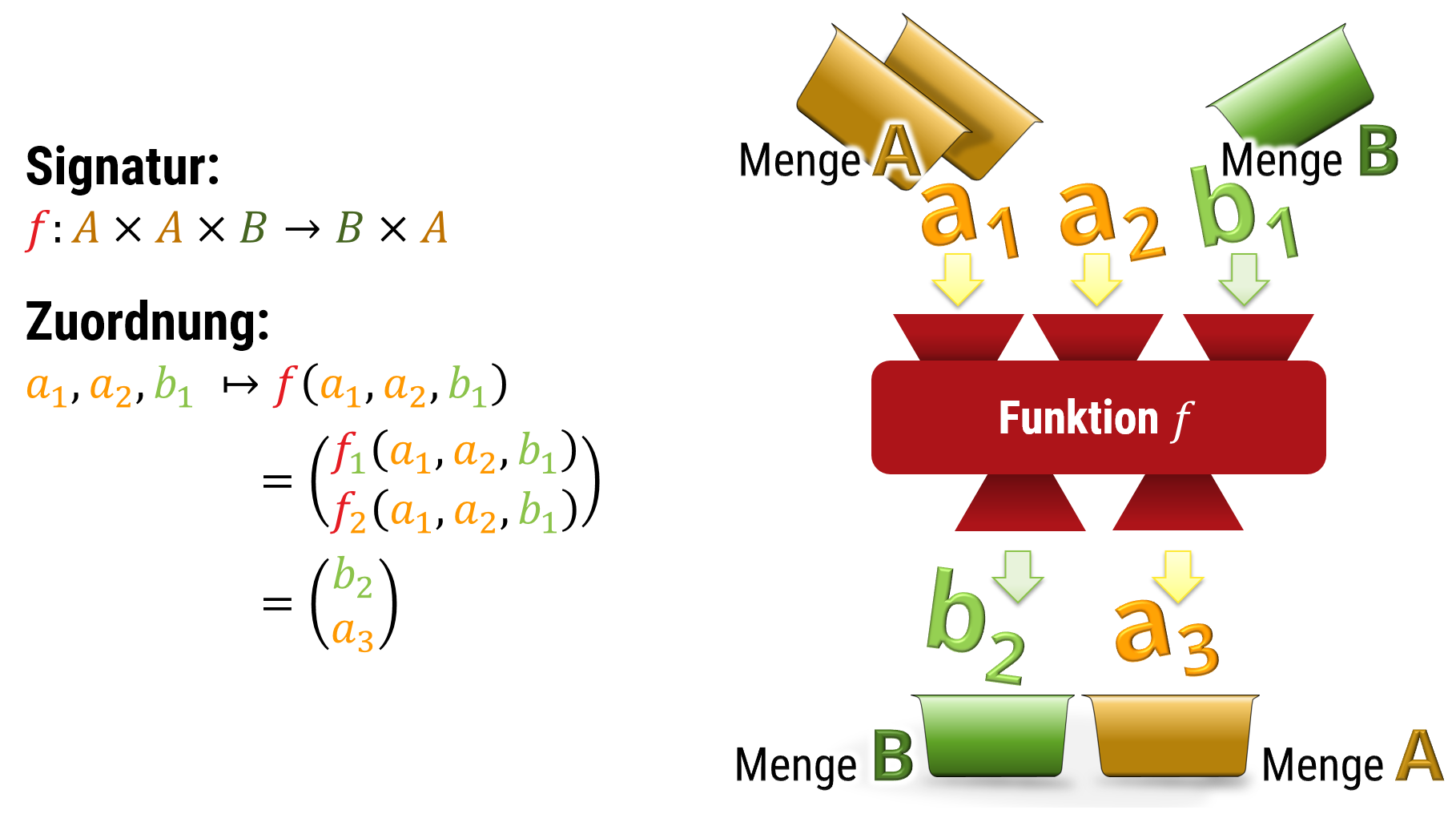



Funktionen können auch komplexere Eingaben (Definitionsmenge) und Ausgaben (Zielmenge) haben. Zum Beispiel kann man das kartesische Produkt nutzen, um Kombinationen von Eingabetype zu konstruieren. Man spricht man auch von „mehrdimensionalen“ Funktionen (insbesondere, wenn Vektoren von kontinuierlichen Mengen wie z.B. reellen oder komplexen Zahlen als Ein- oder Ausgabe auftreten)
Mehrdimensionale Funktionen
Als Definitionsmenge wie auch Zielmenge können beliebige Mengen verwendet werden; dies schließt alle Konstrukte in Kapitel 2 ein. Insbesondere kann man Funktionen mit mehreren Eingaben und dazugehörigen Ausgaben bauen, indem man kartesische Produkte (Tupel, Vektoren, Folgen) als Ein- oder Ausgabe nutzt. Im obenstehenden Bild ist das Prinzip skizziert.
Funktionen höherer Ordnung
Die Art von Mengen, die wir als Ein- oder Ausgaben betrachten, kann beliebig sein. Daher ist es auch möglich, Mengen von Funktionen als Eingabe und/oder Ausgabemengen zu nutzen. In der Informatik nennent man solche Konstrukte Funktionen höherer Ordnung (engl. higher order functions. In der mathematischen Sprache ist die Bezeichnung nicht ganz eindeutig; man spricht hier von Funktionalen (engl. functional) oder gelegentlich auch von Operatoren (engl. operator). Auch der Begriff „Funktor“ (engl. functor) wird manchmal verwendet. Wir bleiben in diesem Skript beim geläufigen Begriff aus der Informatik, da dieser unmissverständlich ist.
Auch jenseits der genauen Benennung sind Funktionen höherer Ordnung eine häufige Quelle von Verwirrung: In der Mathematik werden recht oft Funktionen beschrieben, die wieder Funktionen produzieren (und erst nach Einsetzen weiterer Parameter konkrete Zahlen als Ergebnisse liefern). Nicht selten geschieht das implizit, ohne besonderen Hinweis. Man kommt dann schnell damit durcheinander, was eigentlich gemeint ist. Ein klassisches Beispiel ist der Ableitungsoperator (siehe Kapitel 5): \[ {\color{red}f}({\color{darkblue}x})={\color{darkblue}x}^2+3{\color{darkblue}x}-5 \,\,\,\,\Rightarrow\,\,\,\, \frac{d}{d{\color{darkblue}x}}{\color{functionCol}f}({\color{darkblue}x}):=\left[\frac{d}{d{\color{darkblue}x}}{(\color{functionCol}f})\right]({\color{darkblue}x}):={\color{functionCol}f}'({\color{darkblue}x})=2{\color{darkblue}x}+3 \]
Der Ableitungsoperator \(\frac{d}{d{\color{darkblue}x}}\)\(:\) \(\left\{f: \mathbb{R} \rightarrow \mathbb{R} | f \text { ist differenzierbar}\right\}\) \(\rightarrow\) \((\mathbb{R} \rightarrow \mathbb{R})\) ist dabei eine Funktion, die andere Funktionen als Eingabe nimmt, und die Ableitung (welche ebenfalls eine Funktion ist) als Ausgabe liefert. Die übliche Notation (ohne die oben benutzen Klammern) macht dies aber nicht deutlich; die aus der Schule bekannte Schreibweise mit dem hochgestellten Strich („f-Strich“) bringt dies noch weniger klar zum Ausdruck.
Eindeutigkeit und Mächtigkeit von Mengen
Jede Funktion muß eindeutig festlegen, welches Element der Wertemenge jedem möglichen Element der Definitionsmenge zugeordnet ist. Es spricht aber nichts dagegen, verschiedenen Eingaben die selbe Ausgabe zuzuordnen.Funktionen, bei denen keine Ausgabe doppelt zugeordnet wird, sind umkerbar oder invertierbar. Man nennt solche Funktionen injektiv (engl. injective). Zum Beispiel ist die Abbildung \(x \mapsto e^x\) injektiv. Die Umkehrung liefert die Logarithmusfunktion \(\operatorname{ln}\).
Wie man sieht, kann man umkehrbare Funktionen definieren, die nicht alle Werte der Wertemenge ausnutzen. Dies erfordert, daß die Wertemenge entweder mehr Elemente enthält als die Definitionsmenge, oder daß die beiden Mengen unendlich sind (wie im Beispiel Exponentiation/Logarithmus). Wenn wir Funktionen und die zugehörigen Definitions und Wertemengen so definieren, daß alle Werte angenommen werden können, dann nennt man die Funktion surjektiv (engl. surjective).
Die Kombination, eine Funktion die sowohl surjektiv (alle Ausgabewerte werden erreicht) und injektiv (die Eingabewerte sind eindeutig aus der Ausgabe rekonstruierbar) ist, nennt man bijektiv (engl. bijective).
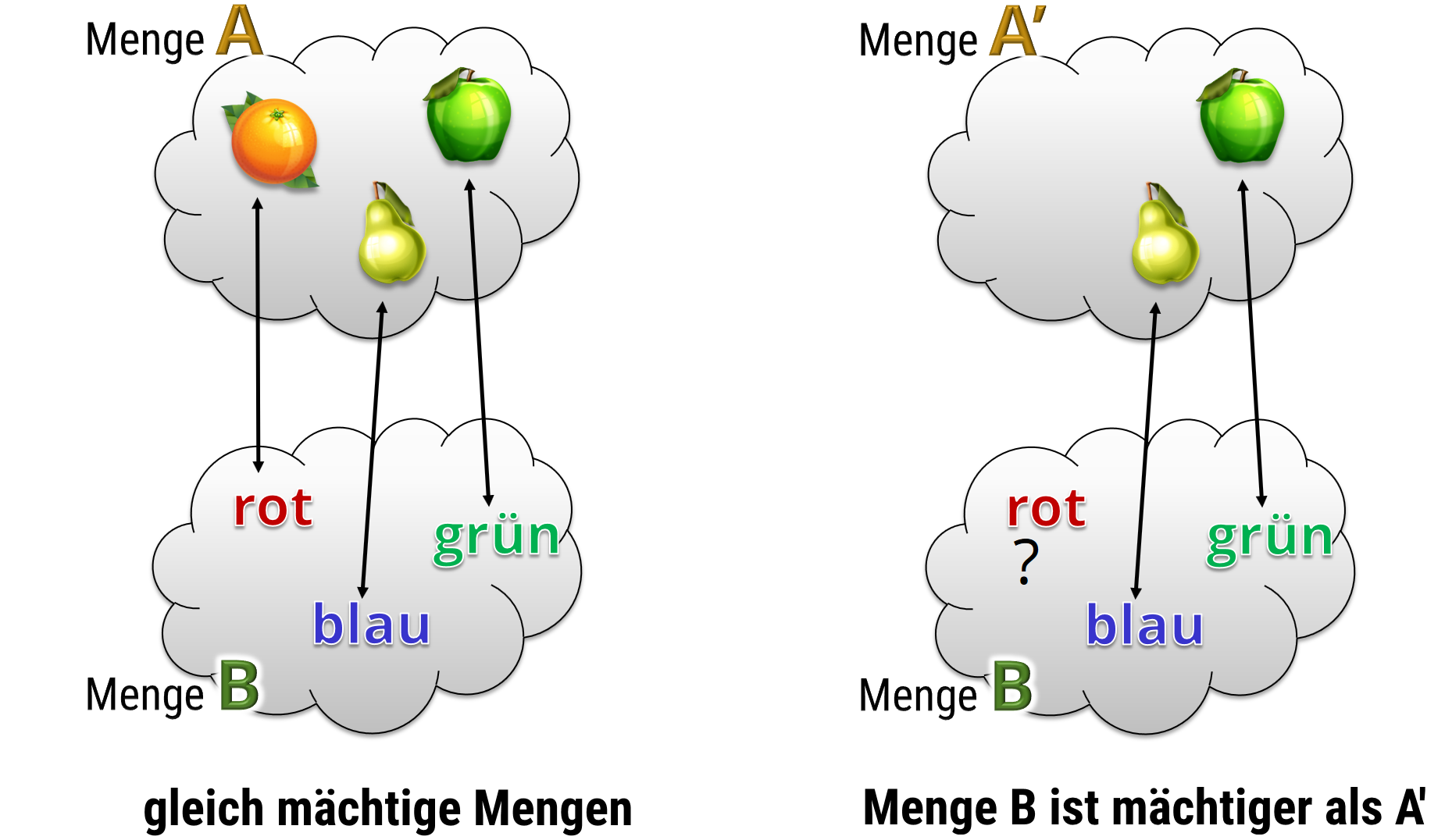



Mächtigkeit von Mengen
Diese Begriffe sind für uns wichtig, da wir damit definieren können, wie „groß“ (mächtig) eine Menge ist. Bei endlichen Mengen vergleichen wir einfach die Anzahl der Elemente (gleich viele = gleich mächtig). Bei unendlichen Mengen geht das aber natürlich nicht so einfach. Daher definieren wir, daß zwei Mengen gleich mächtig (engl. of same cardinality) sind, wenn eine bijektive Abbildung existiert mit der einen Menge als Definitionsmenge und der zweiten als Wertemenge. Diese Definition umfaßt, offensichtlich, automatisch den Fall endlicher Mengen.
Auch bei unendlichen Mengen gibt es verschiedene Mächtigkeiten. Dies (auf den ersten Blick eine theoretische Spielerei) ist für sowohl die moderne Mathematik wie auch die Informatik von enormer Bedeutung. Mehr dazu in Kapitel 3.2
Funktionen in der Informatik
In der (praktischen) Informatik benutzt man den Begriff der Funktion fast genauso wie in der Mathematik. Einziger Unterschied ist, daß wir in der Regel Funktionen nicht einfach so definieren können (nur in der Theorie, nicht beim praktischen Programmieren), sondern wir müssen einen konkreten Algorithmus entwerfen, um die Funktion auch wirklich zu berechnen. Hier gibt es erstmal ein technisches Problem: Ein ein Algorithmus kann in einer Endlosschleife hängenbleiben (das Programm „stürzt ab“). Die übliche Sprachregelung in der Informatik ist daher: „Ein Algorithmus berechnet eine partielle Funktion“. Der Begriff „partielle Funktion“ bedeutet, daß nicht alle Werte der Definitionsmenge zugeordnet werden (müssen); ein Absturz würde mathematische als fehlende Zuordnung interpretiert.
Soweit ist das erstmal ein Problem der Bezeichnung (man könnte ja Parameter, die zu Abstürzen führen, aus der Definitionsmenge einfach ausschließen). Die wichtigere Frage ist, ob jede Funktion, die wir mathematisch sauber definieren können auch berechenbar (engl. computable) ist, ob also ein Algorithmus existiert, der diese Funktion berechnet. Die Antwort ist nein; tatsächlich sind viel mehr Funktionen unberechenbar als berechenbar. Wir beweisen dies im nächsten Unterkapitel.
Damit haben wir einen entscheidenden Unterschied zwischen Funktionen in der (praktischen) Informatik und mathematischen Funktionen: Die berechenbaren Funktionen, für die es Algorithmen gibt, sind eine echte Teilmenge (weniger mächtig) als die Menge der mathematischen Funktionen. Um dies genauer zu verstehen, müssen wir uns die Sache mit den Mengen nochmal anschauen.
Verschiedene Varianten von unendlichen Mengen
Eine Interessante Frage ist, ob alle unendlichen Mengen gleich mächtig sind. Die Antwort hierzu gab Mathematiker Georg Cantor Ende des 19. Jahrhunderts.
Abzählbare Mengen
Zunächst lassen sich unendliche Mengen finden, die unterschiedliche Elemente enthalten und trotzdem gleich groß sind. Ein Beispiel sind die natürlichen Zahlen und die rationalen Zahlen (also die Menge aller Brüche). Hierzu schauen wir uns am besten eine graphische Darstellung von Cantor's „erstem Diagonalargument“ an:
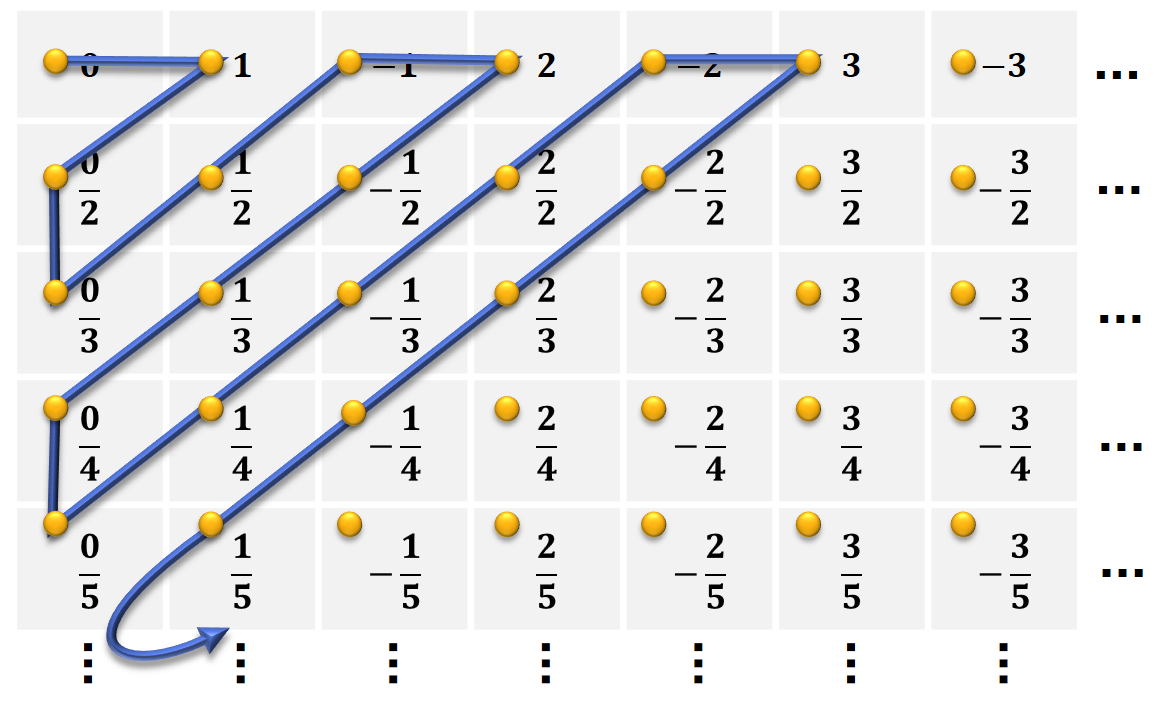



Mit diesem Argument läßt sich auch sehr einfach zeigen, daß alle Paare von natürlichen Zahlen abzählbar sind. Das gilt auch generell für alle \(n\)-Tupel für festes \(n\).
Überabzählbare Mengen
Mit einem sehr ähnlichen Ansatz läßt sich nun beweisen, daß reelle Zahlen nicht abzählbar (überabzählbar) sind, also keine Bijektion in die natürlichen Zahlen existieren kann:
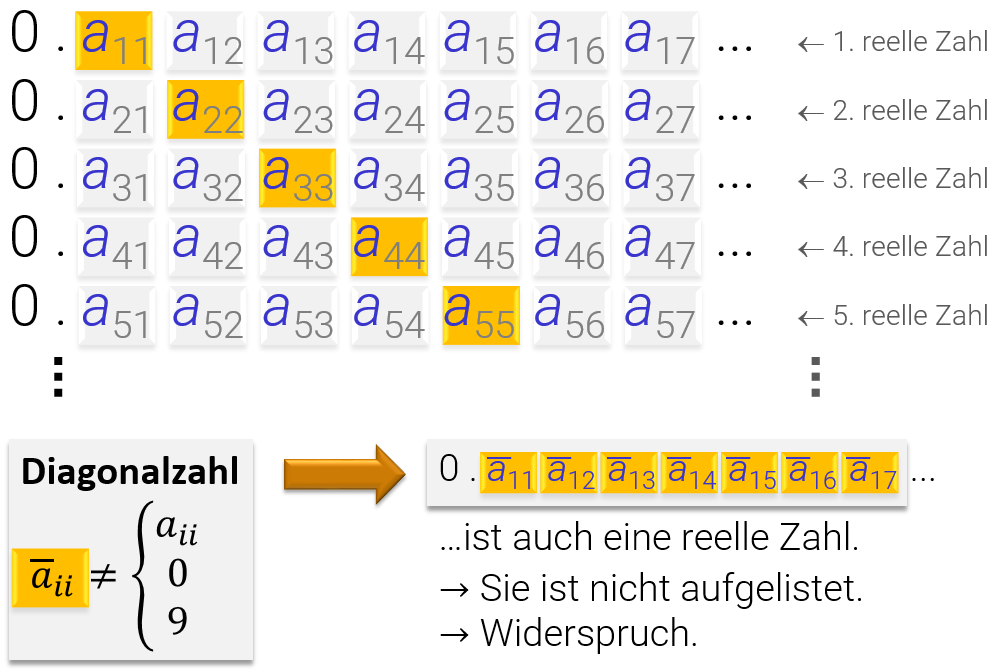



Für abzählbar unendliche Mengen können wir ähnlich vorgehen: Wir bilden abzählbare Bitfolgen. Diese können wir (der Einfachheit halber) ins 10er System konvertieren und dann exakt Cantor's zweite Diagonalisierung durchführen. Für noch mächtigere Mengen benutzt man ein ähnliches Argument mit Axiomatischer Mengenlehre.
Mächtigkeit von Mengen von Funktionen Das gleiche Argument greift auch für die Mächtigkeit von der Menge aller Funktionen, die eine abzählbare Menge von Werten auf eine Wertemenge mit mindestens zwei verschiedenen Werten abbildet: Auch diese Menge aller solcher Funktionen ist überabzählbar. Der Beweis sollte klar sein: Wenn es zwei Werte gibt, können wir jedem Element der Definitionsmenge genau ein Bit zuordnen; danach geht der Widerspruchsbeweis genauso weiter wie bei der Potenzmenge (das ist eigentlich genau das gleiche). Sollte es noch mehr als zwei Werte geben, werden die Funktionen eher mehr als weniger.
Die Grenzen der Erkenntnis und emergente Komplexität
Die oben bewiesenen Sätze erscheinen vielleicht immer noch nicht besonders aufregend, führen aber zu einer der wichtigsten Erkenntnisse der Mathematik überhaupt: Die Gödelsche bzw. Turingsche Unvollständigkeit.
Turingsche Unvollständig
Es ist klar, daß die Menge aller Algorithmen (z.B. in der Form von JAVA- oder Python-Programmen) abzählbar ist; ein Programm wird ja in der Tat durch einen Bitstring kodiert (also eine einzige, sehr große natürliche Zahl, wenn wir es so sehen wollen). Das gleiche gilt für Algorithmen, die wir in Pseudocode aufschreiben (mit unserem Lieblingstexteditor). Die Menge aller Eingaben oder Ausgaben unseres Algorithmus ist ebenfalls eine abzählbar unendliche Menge (wiederum jeweils Teilmengen der Menge aller Bitstrings).
Die Menge aller Funktionen, die aus einer abzählbar unendlichen Menge (Eingaben für einen Algorithmus) auf eine Menge mit mindestens zwei Werten abbildet, ist aber überabzählbar unendlich (wie wir zuvor selbst bewiesen haben). Daß heißt, es gibt mehr Funktionen, als Algorithmen, um diese zu berechenen. Anders gesagt, sind fast alle (mathematische Sprache für „die Menge ist mächtiger“) Funktionen unberechenbar.
Völlig überzeugend ist dieses obige Argument allerdings noch nicht: Es könnte ja sein, daß wir die unberechenbaren Probleme auch gar nicht in mathematischer Sprache formulieren können. Dem ist aber nicht so, wie Turing mit dem berühmten Halteproblem gezeigt hat: Die Frage, ob ein Algorithmus für eine bestimmte Eingabe in einer Endlosschleife hängen bleibt, ist unentscheidbar.
Aus der Unentscheidbarkeit des Halteproblems folgt recht direkt der Satz von Rice: Die Frage danach, ob ein gegebener Algorithmus eine bestimmte, nicht-triviale Eigenschaft hat, ist nicht entscheidbar, wenn wir jeden möglichen Algorithmus als Eingabe zulassen.
Funktionen in Mathematik und in Programmiersprachen unterscheiden sich subtil: An dieser Stelle halten wir fest, daß eine (tatsächlich berechenbare) Funktion in der praktischen Informatik weniger ausdrucksstark ist, als eine allgemeine Funktion in der Mathematik. Jeder Algorithmus definiert auf der Menge von Eingaben, für die er nicht abstürzt, eine mathematische Funktion. Umgekehrt gibt es mathematisch wohldefinierte Funktionen (die sogar praktisch hoch interessant wären), die man nicht mit einem Algorithmus berechnen kann.
Noch eine Bemerkung: Das ganze ist natürlich ein Modell. Wir haben nur bewiesen, daß es für bestimmte Probleme keinen Algorithmus fester Länge gibt, der das gestellte Problem für alle möglichen Eingaben gleichartig löst. Offensichtlich sind alle endlichen Probleme (Eingabelänge beschränkt) grundsätzlich berechenbar (notfalls per Lookup-Table, die natürlich exponentiell in der Eingabe wachsen kann). Da das beobachtbare Universum endlich zu sein scheint, wäre damit alles praktische theoretisch lösbar; die praktische Frage ist daher eher, wie komplex die Lösung wird. Hier zeigt aber die Komplexitätstheorie, daß es Probleme geben muß, die exponentiellen Aufwand erfordern, und damit nicht praktikabel sind.
Gödelsche Unvollständigkeit
Mit sehr ähnlichen Argumenten kann man auch folgenden Satz beweisen: „In jedem mathematischen Axiomensystem das mindestens die natürlichen Zahlen umfaßt gibt es Aussagen, die nicht beweisbar sind.“. Auch hier ist der Trick eine Diagonalisierung: Zunächst ist klar, daß die Menge aller Beweise abzählbar ist (wir können die auch als Bitstrings codieren; im Endeffekt reihen wir ja nur Axiome aneinander in eine Folgerungskette). Etwas schwieriger ist dann, zu zeigen, daß die Menge der korrekten mathematischen Sätze in einem solchen Axiomensystem überabzählbar ist. Dazu wird auch hier ein Diagonalsatz konstruiert, ganz ähnlich wir bei Turing.
Die Grenzen der Erkenntnis
Unsere initial unverdächtige Untersuchung von Mengen verschiedener Mächtigkeit hat zwei (eng verwandte) grundsätzliche Limitierung des menschlichen Denkens und der mathematischen Logik ans Licht gebracht:
- Mathematische Axiomensysteme, die hinreichend komplex sind (natürliche Zahlen werden beschrieben), liefern Strukturen, die aus sich selbst heraus nicht mehr vollständig verstanden werden können, im folgenden Sinne: Es gibt kein endlich langes Argument (Beweis), daß die Struktur aller Konsequenzen unserer Grundannahmen vollständig aufklärt.
- Es gibt unlösbare Probleme in der Informatik: Für manche wohldefinierte Fragen gibt es keinen festen Algorithmus, der immer die richtige Antwort liefert. Insbesondere gilt dies für das Verständnis von Algorithmen selbst. Wir können keinen festen Algorithmus angeben, der für alle möglichen Algorithmen bestimmen kann, wie diese sich verhalten werden. Wir müssen den Algorithmus laufen lassen, und schauen was passiert (und das kann im Allgemeinen beliebig lange dauern; wir wissen nicht mal sicher, ob er anhalten wird.)
Interessant ist, daß die Tatsache, das sowohl Beweise wie auch Algorithmen in abzählbaren, diskreten Schritten operieren müssen, der Grund für die Probleme ist. Daher würde man wohl die selben Resultate für jede Art von Denken bekommen, die mit diskreten Argumenten oder Schritten arbeitet, die jeweils endlich viel Information kodieren. Damit besteht wenig Hoffnung, die Mathematik oder die Informatik hier zu reparieren. Das Denken als solches hat ein Bug, der dafür sorgt, daß wir diese Strukturen nicht mit endlich viel Aufwand vollständig verstehen können.
Church, Turing und emergente Komplexität
Die Church-Turing These
Die Argumente aus dem letzten Abschnitt haben weitreichende Konsequenzen: Zunächst müssen wir uns klar machen, daß alle Modelle in der Physik bis heute so gestaltet sind, daß man sie auf einem Digitalrechner theoretisch mit beliebiger Genauigkeit simulieren kann (ignorieren wir mal das Problem der Interpretation der Quantenmechanik und des Messvorgangs — das spielt für die Simulation keine Rolle, nur für die Natur der Wahrnehmung des Betrachters; auch Metaphysische Fragen des Bewusstseins klammer wir aus). Ignorieren wir das Problem der Approximation (hier könnte eine Überabzählbarkeit lauern), drängt sich der Verdacht auf, daß die Berechnungsmodelle, die wir heute kennen, die mächtigsten sind, die in unserem Universum möglich sind. Ein Python-Skript, dem beliebig viel Speicher zur Verfügung gestellt werden kann, oder ein JAVA oder C++ Programm, für das das gleiche gilt, hat die gleiche Berechnungskraft wie eine „universelle Turingmachine“: Wir können immer die gleichen Probleme lösen, und die unlösbaren Probleme sind mit keinem denkbaren Computer lösbar. Eine Maschine (oder Programmiersprache) mit dieser Berechnungskraft nennt man auch Turing-vollständig (engl. Turing-complete).
Umgekehrt kann man mit physikalischen Gesetzen Computer bauen (unsere Rechner bestehen ja aus Universum). Das heißt, daß die Turingsche Unvollständigkeit auch hier gilt: Wir können kein endlich langen Algorithmus schreiben, mit dem wir verstehen können, wie ein unbeschränktes Stück Raum sich über die Zeit entwickeln wird. Wir können es zwar simulieren, und verfolgen was passiert. Einen festen Algorithmus um Aussagen beliebig weit in die Zukunft zu machen, gibt es aber nicht. Für endliche Probleme sind wieder im allgemeinen exponentielle Kosten in der Eingabekomplexität zu erwarten — praktikabel ist das also auch nicht.
Etwas polemisch formuliert, könnte man die Hyptothese der prinzipiellen Simulierbarkeit des Universums auf einem Rechner zusammen mit den Unentscheidbarkeitsresultaten auch eine „no-cheating Hypothese“ nennen. Wenn die Prämisse des Films Die Matrix (oder vieler anderer Gedankenspiele in diese Richtung) stimmt, und wir eigentlich in einer Simulation oder einem Computerspiel leben, dann haben die Programmierer des Spiels eine Sicherung eingebaut, daß man nicht cheaten kann: Man kann nicht mit endlich viel Aufwand alles vorhersagen, was jemals passieren wird. Die einzige Möglichkeit, alles zu sehen, ist das Spiel bis zu Ende zu spielen (oder zu simulieren). Das ist natürlich kein Beweis für die Simulationshypothese (eine perfekte Simulation könnte man ohnehin nicht beweisen), sondern eher eine Polemik, die man sich besser merken kann als all die Diagonalisierungsbeweise.}
Emergente Komplexität
Dieses Phänomen ist allgemein (egal ob für Software, für mathematische Axiomensysteme, für Modelle in empirischen Wissenschaften oder für reale Phänomene in unserer Welt und unserem Universum) als emergente Komplexität (engl. emergent complexity) bekannt: Aus sehr einfachen Regelsystemen (Turingvollständig: man kann einen Computer damit simulieren) können beliebig komplexe Muster entstehen, die sich nicht mehr mit Algorithmen fester Komplexität vollständig analysieren lassen.
Diese Beobachtung löst ein scheinbares Paradox auf: Obwohl die Gesetzte des Universums relativ einfach zu sein scheinen, entstehen sehr komplexe Strukturen als ein emergentes Phänomen. Wenn wir mit der Bürokratie kämpfen, durch blöde Übungsaufgaben frustriert sind oder traurig sind, wenn unsere Lieblingswebseite mit süßen Katzenbildern mal nicht erreichbar ist, dann ist dies alles wahrscheinlich die Folge von nur einer handvoll sehr einfacher Regeln und ca. 13.7 Milliarden Jahren Rechenzeit und \(4.2 \times 91^3\)-Kubiklichtjahren Speicher.
Eine Modellhierarchie
Wenn wir nun zurückblicken auf die verschiedenen Arten von Modellen, die wir in Kapitel 2 kennengelernt haben, so sehen wir eine Hierarchie:
mathematische Modelle \(\supsetneq\) Modelle der praktischen Informatik \(\supsetneq\) Physik \(\supseteq\) empirische Modelle
- Mathematische Modelle: Sind reine Konstrukte der menschlichen Vorstellungskraft, nur beschränkt durch die Gesetzte der Logik. Wir können hier alles definieren was wir wollen, und nach Beweisen suchen, die uns die Folgen der Annahmen zeigen. Manche Folgen sind nicht beweisbar (obwohl sie wahr sind: Gödel). Es ist auch denkbar, daß die Axiome sich gegenseitig widersprechen, aber kein Beweis für diese Tatsache existiert (auch dies kann man mit einem Gödelschen Argument zeigen).
- Algorithmen (Modelle in der praktischen Informatik): Diese umfassen alles, was man mit einem Computer berechnen kann. Dies ist eine echte Teilmenge von dem, was man mathematisch beschreiben kann.
- Physikalische (empirische) Realität: Nicht alles, was man berechnen kann, existiert auch wirklich im Universum (zum Glück). Umgekehrt gehen aber alle existierenden Theorien davon aus, daß man die Modelle auch simulieren kann (zumindest mit beliebig hoher Genauigkeit; ob dies ein Problem für den Berechenbarkeitsbegriff ist, hängt davon ab, ob die Modelle am Ende inhärent diskret oder „echt“ kontinuierlich sind; in letzterem Falle könnte die Church-Turing Hypothese zumindest prinzipiell doch noch in Probleme geraten).
Repräsentation von Funktionen in Programmiersprachen
Wie können wir die verschiedenen berechenbaren Funktionen in Programmiersprachen umsetzen? Diese Frage ist die Kernfrage des gesamten Gebietes der Informatik als solche. In diesem Unterkapitel können das natürlich nicht umfassend beleuchten. Statt dessen schauen wir uns an, welche Abstraktionen für das Konzept der Funktion in Programmiersprachen benutzt werden und deren Beziehung zum mathematischen Formalismus.Code vs. Funktionen
Auf einem von-Neumann-Rechner, und das sind praktisch alle, die wir heute benutzen, werden Berechnungen durchgeführt, indem der Inhalt von Speicherzellen mit verschiedenen Befehlen manipuliert wird. Die Ausführung eines Algorithmus beginnt damit, daß die Eingabe in einigen dieser Speicherstellen kodiert abgelegt wird, und endet damit, daß eine andere Teilmenge der Speicherstelle eine Kodierung des Ergebnisses enthält. Das Programm, welches ausgeführt wird, ist ebenfalls in einem Speicherbereich kodiert abgelegt. Befehle sind also ebenfalls Daten. Dies ist übrigens grundsätzlich möglich: Eine universelle, Turing-mächtige Maschine zeichnet sich genau dadurch aus, daß man mit Ihr einen Interpreter schreiben kann, der eine Kodierung eines beliebigen Algorithmus als Daten im Speicher hält und dann die Ausführung simuliert. Dies gilt unabhängig davon, ob das Maschinenmodell ein von-Neumann Modell ist.Wir können also eine von-Neumann-Maschine (anders gesagt: einen Computer) dazu benutzen, um Funktionen zu berechnen. Und wenn die Church-Turing Hyptothese stimmt, dann haben wir damit alle berechenbaren Funktionen modelliert. Um strukturiert zu programmieren, möchten wir die Berechnungen aber stärker ordnen. Dazu bieten fast alle gängigen Programmiersprachen das Konzept von Funktionen (manchmal auch: „Prozeduren“, oder „Unterroutinen“) an.
Mathematische Funktionen
Mathematische Funktionen beschreiben eine feststehende Zuordnung von Eingabe- zu Ausgabewerten. Diese ist nur berechenbar, wenn wir die Zuordnung mit eine (Turing-mächtigen) Maschine auch tatsächlich bestimmen können. Berechenbare Funktionen, formuliert in rein mathematischer Sprache, bestehen daher aus drei Grundbausteinen:
- Elementare Funktionen: Es gibt Zuordnungen, die so einfach sind, daß wir sie direkt in Hardware bauen könn(t)en (z.B. einfache logische Verknüpfungen, wenn wir in Transistoren und Gattern denken, oder einfache arithmetische Befehle, wenn wir eine moderne CPU voraussetzen). Damit sind diese berechenbar.
- Zusammengesetzte Funktionen: Die zweite Möglichkeit ist, Funktionen miteinander zu kombinieren. Das heißt, wir teilen eine komplexe Berechnung in mehrere Schritte auf, die wir als hierarchische Komposition von Funktionen aufschreiben: \({\color{darkblue}x} \mapsto {\color{darkblue}x}^2 - {\color{darkblue}4} \cdot {\color{darkblue}x}\) wird dann z.B. zu \([+]\Big( [\times]\big({\color{darkblue}x},{\color{darkblue}x}\big) , [-]\big( [\times]\left({\color{darkblue}4},{\color{darkblue}x}\right) \big) \Big)\),
wobei die elementaren Funktionen als Operatoren in eckigen Klammern geschrieben sind.
- Rekursion: Die dritte Möglichkeit ist, wenn man möchte, ein Spezialfall der zweiten: Wir erlauben, daß Funktionen sich selbst rekursiv benutzen. Dabei müssen wir natürlich darauf achten, daß sich die Argumente bei der wiederholten Auswertung so verändern, daß wir keine endlose Schleife definieren. Beispiel: \(({\color{darkblue}x},{\color{grey}n}) \mapsto\) \({\color{darkblue}x}^{\color{grey}n}:= \begin{cases} {\color{darkblue}x}\text{, falls } {\color{grey}n}=1 \\ {\color{darkblue}x}\cdot {\color{darkblue}x}^{({\color{grey}n}-1)}\text{, sonst} \end{cases}\)
Diesen Ansatz kann leicht auf einem Rechner simulieren (mit Funktionsaufrufen, elementaren Funktionen, und einem Stack-Speicher für die Rekursion), und man kann beweisen, daß er Turing-mächtig ist. Diese Idee, in der Informatik auch als Lambda-Kalkül bekannt, ist die Grundlage von (streng) funktionalen Programmiersprachen wie Haskell oder ML.
Funktionen in imperativen Sprachen wie JAVA, C++, oder Python
Die meisten Programmiersprachen definieren Funktionen als Code-Blöcke, die aufgerufen werden können. Dabei werden fest definierte Eingabe- und Ausgabeparameter und können ihrerseits wieder Funktionen aufrufen (auch rekursiv). In diesem Sinne erfüllen sie alle Anforderungen des Lambda-Kalküls. Zusätzlich erlauben sie aber noch mehr: Wir können auch andere Variablen direkt verändern, die nicht als Parameter übergeben wurden (sogenannte Seiteneffekte). Dies können globale Variablen sein (was als schlechter Stil verschrieen ist) oder, in der objektorientierten Programmierung, Objekte, die mit Funktionen fest verknüpft sind (man schränkt also die Seiteneffekte ein). Eine weitere Möglichkeit ist die Veränderung lokaler Variablen, die aber außerhalb der Funktion nicht sichtbar sind. Dies ist nützlich, da man damit Schleifen realisieren kann, ohne Rekursion anwenden zu müssen.
Eine Funktion entspricht sehr genau dem mathematischen Modell, wenn wir keinerlei Seiteneffekte zulassen, und auch jeden Zugriff auf Daten verbieten, die nicht explizit als Parameter übergeben wurden. Damit bleibt leider auch nur Rekursion als einzige Möglichkeit, den Kontrollfluß im Programm zu steuern. Diese Einschränkung ist als strenge oder „reine“ funktionale Programmierung bekannt. Hauptvorteil ist die „referentielle Transparenz“, das heißt, daß man aus dem Aufruf mit gleichen Parametern sicher voraussagen kann, was das Ergebnis sein wird. verschiedene Funktionsaufrufe beeinflussen sich nicht gegenseitig. Man kann diese Vorteile immer noch garantieren, wenn man nur den Zugriff auf Parameter (lesend), Rückgabewerte (schreibend) und lokale Variablen (beliebig) erlaubt. Dieses Modell von referentieller Transparenz wird zum Beispiel in der (primär imperativen) Programmiersprache D) mit dem Schlüsselwort „pure“ unterstützt. In Sprachen wie Python, JAVA oder C/C++ ist es möglich, einen solchen Programmierstil zu nutzen (mit mehr oder weniger Unterstützung durch die Sprache selbst). Es gilt inzwischen als guter Stil, Funktionen in größeren Programmsystemen wann immer möglich zumindest in dieser Form (die weiterhin Schleifen und all die Bequemlichkeiten imperativer Programmierung gestattet) referentiell transparent zu gestalten, und nur eine möglichst kleine Menge von Funktionen zu definieren, die Variablen global zu ihnen verändern können. Grund ist, daß Seiteneffekte besonders anfällig für Programmierfehler sind. Außerdem werden Optimierungen wie automatische Parallelisierung erschwert oder sogar unmöglich.
Funktionen höherer Ordnung
Um Funktionen als Werte der Berechnung zu nutzen, gibt es zwei Möglichkeiten. In manchen Programmiersprachen stehen beide, in anderen nur die zweite zur Vorfügung:- Programmcode als Daten: In interpretierten Sprachen (dazu gehört Maschinensprache, wenn man die CPU als Interpreter auffaßt), ist es einfach möglich, Homoikonizität zu erreichen. Das heißt, das Programmcode direkt als Daten des Programms gespeichert und auch ausgeführt werden kann. Neben Maschinensprache haben auch Programmiersprachen wie LISP, Smalltalk oder Python die Eigenschaft, daß man jederzeit Daten eines Programms als Code interpretieren und direkt ausführen kann (in Python kann man z.B. einen String einfach via „
exec()“ oder „eval()“ als Python-Code interpretieren). Besonders einfach ist dies in LISP-Dialekten; hier ist das Datenformat für Code (Funktionen) und Daten (kodiert als Funktionen) exakt gleich. - Funktionszeiger: Kompilierte Sprachen wie C/C++, Pascal, oder JAVA/C# erlauben dies nicht so einfach, da man Code erst in Maschinensprache (oder Bytecode) übersetzen muß. Hier werden Funktionszeiger (oder objektorientierte Abstraktionen davon) genutzt, die nur auf eine fixe Auswahl von zur Übersetzungszeit bekannten und bereits übersetzten Stücken Programmcode verweisen können. Über Kompilierung zur Laufzeit und dynamisches Laden von Bibliotheken kann man aber auch in diesen Systemen neuen Code zur Laufzeit erzeugen. Manche Umgebungen, wie z.B. C# bzw. „.net“ stellen hierfür spezielle Werkzeuge bereit.
Funktionszeiger
In hardwarenahen Sprachen wie C/C++ oder modernen Pascal Dialekten (z.B. MODULA-2, Delphi/ObjectPascal) kann man Zeiger auf Funktionen direkt als Datentypen verwenden. Streng objektorientierte Sprachen wie JAVA erlauben dies nicht; hier nutzt man ein Funktionsobjekt mit einer einzelnen Methoden; durch Vererbung können nun verschiedene, austauschbare Funktionszeiger erzeugt werden. Python im Prinzip arbeitet genauso: Funktionen sind hier grundsätzlich immer Objekte (die dynamische Typisierung der Sprache sowie spezielle Unterstützung für funktionale Programmierung machen es aber sehr einfach, diese zu benutzen). Zusätzlich ist hier dynamische Codegenerierung relativ einfach möglich.
Funktionale Programmierung
(Rein) funktionale Sprachen erlauben nur referentiell transparente Funktionen im mathematischen Sinne. Zusätzlich bringen diese ein Repertoire von speziell darauf abgestimmten Programmiertechniken mit. Dazu gehören Lambda-Ausdrücke (die Konstruktion von Funktionen ohne extra Deklaration), Funktionen als Datentypen (damit automatisch: Unterstützung von Funktionen höherer Ordnung), partielle Auswertung von Funktionen (man setzt nur einen Teil der Parameter fest) oder Lazy-Evaluation (Funktionen werden erst berechnet wenn der Wert benötigt wird).
In imperativen bzw. objektorientierten Systemen kann man Funktionen als Datentypen repräsentieren, indem man Funktionsobjekte definiert, die Zeiger auf Funktionen zusammen mit Parametern halten. Diese können dann als Parameter oder Rückgaben von Funktionen (höherer Ordnung) dienen. Partielle Anwendung besteht lediglich darin, die Parameter der Funktionsobjekte partiell auszufüllen (und als festgelegt zu markieren). Für Lazy-Evaluation wird z.B. über Iteratorobjekte simuliert, die in ihrem internen Zustand speichern, wie tief man in die Auswertung shierarchie abgestiegen ist.
Moderne Programmiersprachen (darunter auch Python, modernes C++ und die neusten Versionen von JAVA) bieten direkte Sprachunterstützung, die die Nutzung von funktionalen Methoden und Designpatterns deutlich vereinfachen. Lediglich die strenge referentielle Transparenz wird nicht erzwungen sondern bleibt optional (was aber auch für viele funktionale Sprachen wie Scala, LISP oder F# gilt).
Zusammengefaßt
Mit berechenbaren, potentiell rekursiven Funktionen im mathematischen Sinne kann man beliebige Algorithmen beschreiben. Dieses Programmiermodell bezeichnet man in der Informatik als (streng/rein) funktionale Programmierung. Auf einem von-Neumann Rechner ist die rein Funktionale Programmierung (keine Seiteneffekte, Kontrollfluß wird nur durch Fallunterscheidungen und Rekursion kontrolliert) eine Einschränkung gegenüber allgemeinen Funktionen oder Prozeduren wie sie aus imperativen Programmiersprachen bekannt sind. Dies hat sowohl Vor- und Nachteile für die Softwareentwicklung, je nach Anwendungsszenario. Ein nützliches Werkzeug in Mathematik wie Informatik sind Funktionen höherer Ordnung, also Funktionen, die Funktionen als Ein- und/oder Ausgaben nutzen. Dies ist in fast allen verbreiteten Programmiersprachen möglich, und wird in funktionalen Sprachen besonders gut unterstützt. Objektorientierung ist ein Spezialfall davon: Da Datenobjekte über virtuelle Methoden mit Code verbunden sind, macht die Übergabe von Objekten an Methoden diese automatisch zu speziellen „Funktionen höherer Ordnung“ (und das ist ein entscheidener Grund für die Flexibilität dieses Programmiermodels).
Übungen zur Vorbereitung
Bearbeiten Sie zur Vorbereitung auf die Vorlesung folgende Aufgaben:
- Beweisen Sie den Satz von Rice, indem Sie ihn auf die Unentscheidbarkeit des Halteproblems zurückführen.
- Warum ist die Menge aller n-Tupel mit Komponenten aus abzählbaren Mengen wieder abzählbar? Skizzieren Sie einen Beweis.
- Entwerfen Sie eine Klasse in JAVA, C++ oder Python, die beliebige Funktionen als Datentypen repräsentiert (der Code ist zur Übersetzungszeit komplett bekannt). Vermeiden Sie eingebaute Funktionalität (Standardbibliotheken oder Sprachfeatures) zu nutzen, die dies direkt unterstützen. Bauen Sie statt dessen nur auf Klassen/Objekten und virtuellen Methoden auf.