Grundlagen I: Modelle, Mengen

Nun zum eigentlichen Thema. Mathematische Modellierung. Wir müssen hier erstmal klären, welche verschiedenen Arten von Modellen es eigentlich gibt, und wo die subtilen Unterschiede liegen.

Modelle in Mathematik, Naturwissenschaften und Informatik

Mathematische Modelle

Grob gesagt interessiert sich die Mathematik für Aussagen. Wir wollen wissen, ob eine Aussage richtig oder falsch ist, und das absolut sicher (und unabhängig von Beobachtungen in der realen Welt, nur basierend auf reiner Logik). Ein mathematisches Modell besteht grundsätzlich aus Axiomen aus denen sich Folgerungen ergeben: Axiome sind Annahmen, die wir als wahr voraussetzen

, und nicht weiter hinterfragen. Daraus versuchen wir möglichst viele bzw. nützliche Aussagen zu folgern, die sich zwangsweise aus der Annahme der Axiome ergeben.

Die meisten mathematische Modelle benutzen Axiome, die Zahlensysteme und Rechenregeln definieren (in der Form von Mengen und Funktionen; mehr dazu im weiteren Verlauf). Im Zentrum des Interesses steht aber immer die Struktur: Es soll bewiesen werden, daß die Modelle bestimmte Eigenschaften haben. Berechnungen tatsächlich durchzuführen spielt (vor allem in der höheren Mathematik an der Universität) oft eine geringere Rolle.

Algorithmen in der Informatik

In der praktischen Informatik steht oft etwas anderes im Mittelpunkt der Aufmerksamkeit: Hier geht es vor allem darum, Programme zu entwickeln, die konkrete Probleme lösen. Daß heißt, im Zentrum des Interesses steht es, eine Berechnung durchzuführen. Wir wollen hier Rechenvorschriften entwickeln, die nach einem festen Schema ablaufen (einem Algorithmus) und am Ende ein gewünschtes Ergebnis erzielen .

Empirische Modelle

Es lohnt sich an dieser Stelle auch kurz auf Modelle aus empirischen Wissenschaften wie z.B. der Physik zu schauen (wir nehmen im Folgenden immer die Physik als Beispiel, weil sich hier alles formal modellieren läßt; in Erweiterung gilt dies natürlich auch für andere empirische Wissenschaften, wie Chemie, Biologie, Wirtschaftswissenschaften, Soziologie, Linguistik, und viele andere Disziplinen, soweit diese die formale Modelle, also Modelle in mathematischer Sprache, von realen Phänomenen bilden).

In den empirischen Wissenschaften geht es darum, mathematische Modelle zu bilden, und oft auch Algorithmen zu finden , die reale Phänomene abbilden. Die wesentliche Einschränkung steht am Ende des letzten Satzes: die betrachteten Modelle müssen etwas mit der Realität zu tun haben müssen. Was kennzeichnet ein Modell, dass "die Realität abbildet"? Sehr schön auf den Punkt gebracht hat dies der Physiker Heinrich Hertz in seinen Principien der Mechanik (1894):

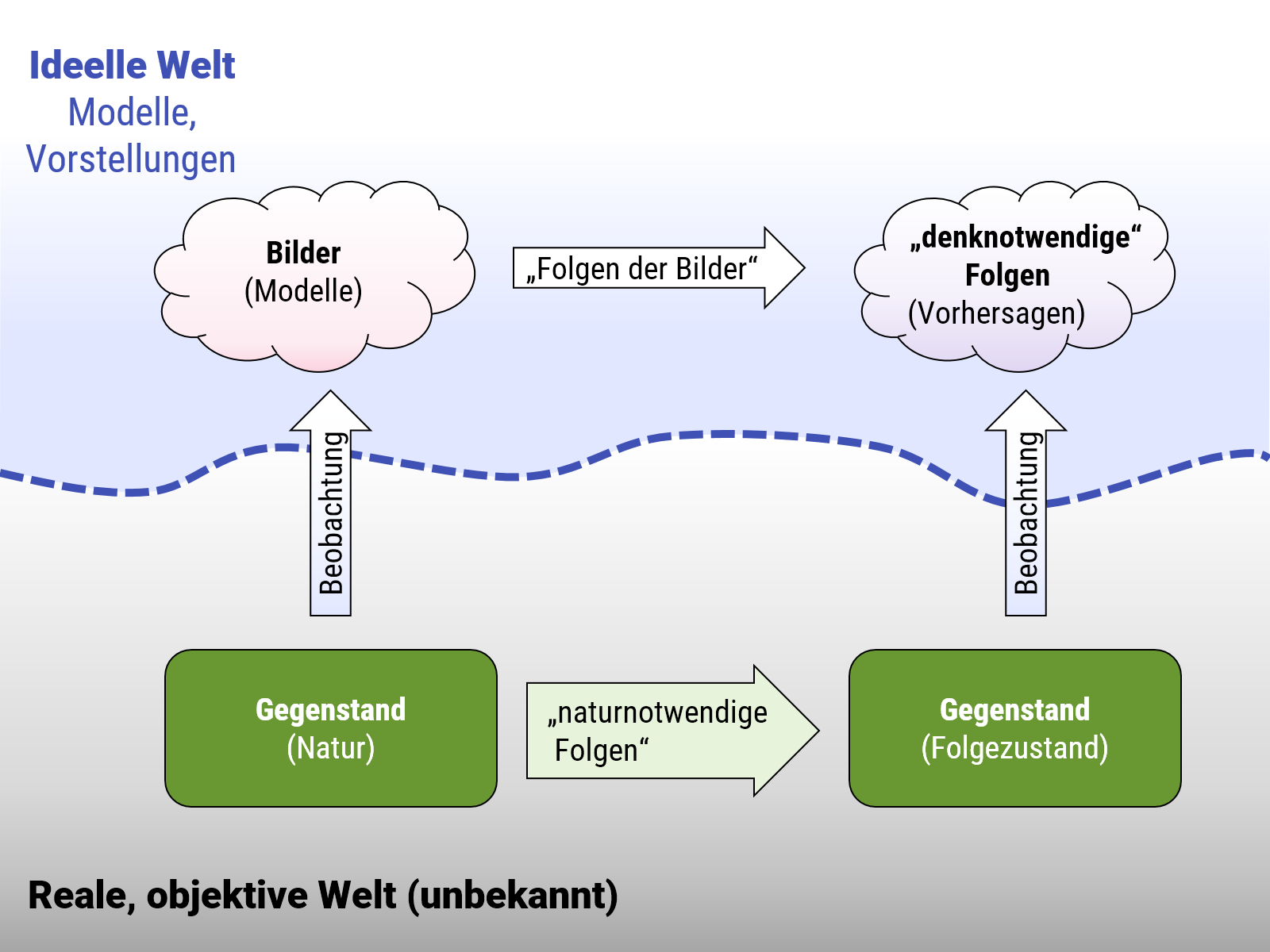
Wir machen uns innere Scheinbilder oder Symbole der äußeren Gegenstände, und zwar machen wir sie von solcher Art, daß die denknotwendigen Folgen der Bilder stets wieder die Bilder seien von den naturnotwendigen Folgen der abgebildeten Gegenstände

In dieser Betrachtung sind Modelle nur dann nützlich für die Beschreibung realer Phänomene, wenn sie richtige Voraussagen über das reale Verhalten machen (also Informationen richtig voraussagen, die man nicht schon komplett in Form von Beobachtungen vorab in das Modell reingesteckt hat). Anders gesagt: Der Unterschied zwischen einem allgemeinen Modell (mathematisch oder algorithmisch) und einem empirischen wissenschaftlichem (z.B. physikalischem) Modell ist, daß es die Realität beschreibt. Dies machen wir daran fest, daß das Modell Voraussagen macht, die in der Realität tatsächlich eintreffen.

Modelle aus Beobachtungen — gute und schlechte

Ein Modell, das Voraussagen macht, die Beobachtungen widersprechen, ist ein schlechtes Modell (auch wenn es in sich mathematisch konsistent ist, und effizient in einen Algorithmus umsetzbar; empirisch nützt das trotzdem nichts). Die Gegenfrage ist interessanter: Ist jedes Model, daß zuverlässige und genaue Voraussagen macht ein gutes Modell? In wie weit können wir uns darauf verlassen, in weiteren Anwendungen des Modells immer noch gute Voraussagen zu bekommen. Viele Modelle nutzen auch innere Hilfskonstruktion, postulierte Mechanismen, die man nicht direkt beobachten kann. Ist es gerechtfertigt, auch an alle Details dieses Modells glauben? Bei einem "guten" Modell würden wir das erwarten.

Es stellt sich heraus, daß eine gute Vorhersagegenauigkeit auf einem beschränkten Satz an Beobachtungen nicht ausreichend ist, um ein gutes Modell zu erhalten. Der Grund ist, daß es in der Regel sehr viele, verschiedene Modelle gibt, die alle einen beschränkten Satz an Beobachtungen eines Phänomene korrekt voraussagen. Diese unterscheiden sich jedoch darin, wie gut diese "generalisieren", also auch unter leicht geänderten Randbedingungen noch richtige Voraussagen machen. Innerhalb des Models postulierte Mechanismen, die nicht direkt beobachtet werden können, würden hier als Vorhersagen gewertet, die unter allgemeineren Rahmenbedingungen noch gelten müssen (wenn man ein neues Experiment findet, z.B. einen größeren Teilchenbeschleuniger, mit dem man diese Dinge doch beobachten kann). Eine ganz entscheidene Richtlinie ("Occam's Razor") in allen modernen Wissenschaften ist, daß Modelle, die besonders einfach sind, in der Regel besser generalisieren als komplexere Modelle, die mit mehr Aufwand an die Daten angepaßt werden müssen; das Risko das die Details nicht stimmen und nur "hingebogen" sind, wird um so größer, je komplexer das Modell ist (also mehr Mechanismen, mehr Parameter, etc.). Mehr Details dazu, bei Interesse, in der Textbox unten.

Induktive Schlüsse und Occam's Razor

Das Problem der Induktion

Ein allgemeines Modell aus der Beobachtung von einigen Beispielen (die nicht alle möglichen Situationen abdecken) abzuleiten, nennt man das Problem der " Induktion " (im Gegensatz zur " Deduktion ", dem logischen Schluß aus gesicherten Informationen oder Axiomen; mathematiker arbeiten Deduktiv, Naturwissenschafter in der Regel induktiv). Ein induktiver Schluß ist nötig, wenn wir allgemeine Gesetze für Phänomene aus Beobachtungen bilden wollen (z.B. Naturgesetze in der Physik, wie die Quantenelektrodynamik oder die Newtonsche Mechanik). Da wir hier nicht alle möglichen Voraussagen des Modells direkt empirisch bestätigen können, sondern nur einige Beispiele sehen, spielt es eine Rolle, wie gut das Modell selbst ist: Unter alle betrachteten Modelle, die die Beobachtungen gleich gut erklären, gibt es immer noch "bessere" und "schlechtere".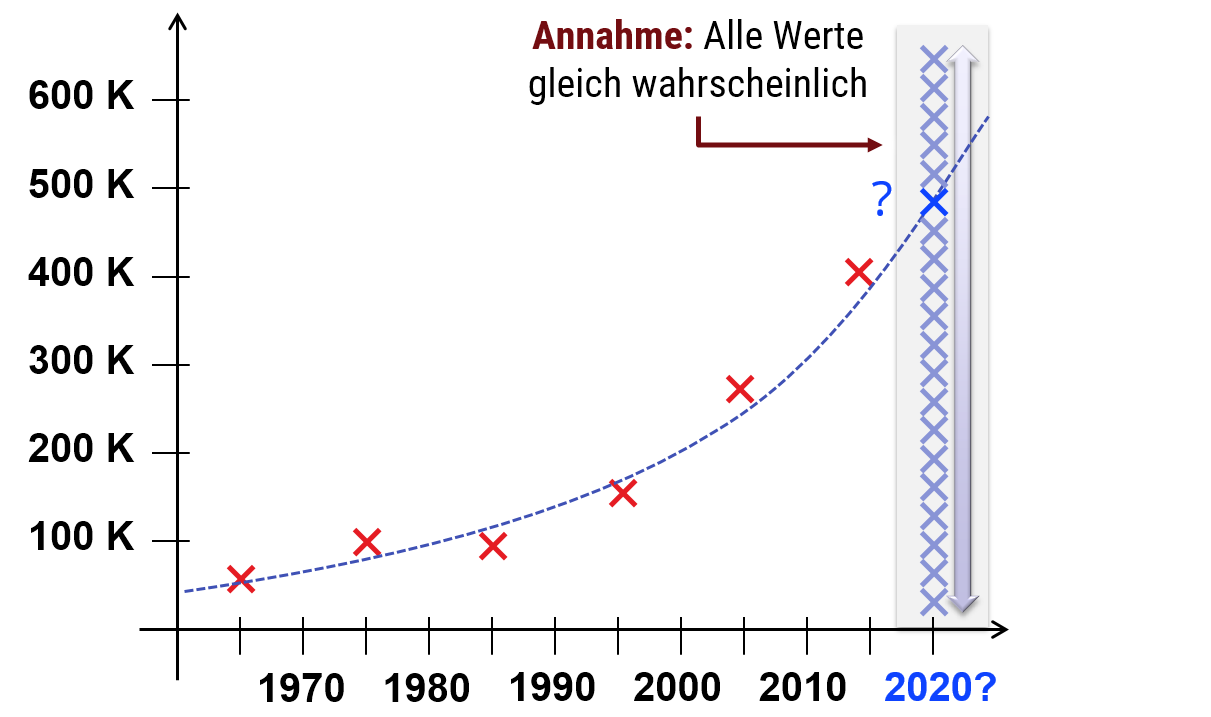

"No free lunch" - Induktion geht nicht mit reiner Logik: Grundsätzlich setzt Induktion voraus, daß wir annehmen, daß die Welt nicht beliebig kompliziert ist. Nehmen wir an, wir haben 10 Messwerte gemessen (z.B. mittleren Preis von Wohnungen pro Quadratmeter in Mainz von 2006 - 2016). Nun können wir versuchen, vorauszusagen, welche Preise 2017 zu erwarten sind. Wenn wir annehmen, daß Preise langsam und stetig schwanken (und meist steigen), läßt sich sicher eine Prognose machen, die mit einer gewissen Wahrscheinlichkeit eine gewisse Genauigkeit erreicht. Falls wir keine Grundannahmen machen (also z.B. annehmen, daß alle Preise zwischen 1 - 1000€ pro Quadratmeter gleich wahrscheinlich sind bzw. das echte Ergebnis reiner Zufall ist und keiner Gesetzmäßigkeit unterliegt), so wird keine Prognose funktionieren. Egal wie wir versuchen zu schätzen, es geht immer mit gleicher Wahrscheinlichkeit schief. Diese Einschränkung für Induktive Schlüsse ist auch als " no free lunch theorem " bekannt. Induktion setzt also immer voraus, daß wir annehmen, das die zu modellierende Welt in gewisser Weiser "einfach" ist (also sich nicht, im Extrem, sich völlig zufällig und damit unvorhersagbar verhält, sondern "regelmäßiger"). Diese Annahme nennt man auch "induktiver Bias" (oder im statistischen Lernen "prior [assumption]"). Je mehr wir unabhängig von Beobachtungen bereits über das Phänomen wissen, das wir beobachten, desto besser können die Vorhersagen werden.

Occam's Razor

Was aber kann eigentlich noch schiefgehen, wenn die bisher beobachteten Daten genau getroffen werden? Man kann man sich die Fallstricke der Induktion an ein einfaches Beispiel veranschaulichen (die Idee ist an ein ähnliches Beispiel aus einem Vortrag von David Deutsch angelehnt, " A new way to explain explanation " ; der Vortrag behandelt genaue dieses Thema und ist zur Vertiefung sehr zu empfehlen):

Beispiel für ein schlechtes Modell mit präzisen Vorhersagen

Nehmen wir an, es gibt eine alte Mythologie (als längst vergangenen Zeiten, vor Jahrtausenden erdacht, in einem kleinen Dorf am Rhein), die den Wechsel von Tag und Nacht damit erklärt, daß Götter der Dunkelheit und des Lichtes einen immerwährenden Kampf um die Oberhand im Himmel über uns austragen. Die Geschichte ist involviert (Eifersucht, Kriege, Mord und Totschlag; wir wissen ja, wie solche Geschichten liebevoll gestaltet werden können), sagt aber genau voraus, daß sich Tag und Nacht genau im 24h Rythmus abwechseln, und daß die Nächte im Winter länger werden (auch hier läge der Grund in Streitigkeiten der Obrigkeiten hoch über unseren Köpfen; man kann die Kriege im Reich der Götter hinreichend ausschmücken, um auch numerisch genau die Tageslängen zu den Jahreszeiten zu erhalten, passend für an dem Ort, an dem die Geschichte erfunden wurde).
Im Sinne der obigen Anforderung (korrekte Voraussagen), wären wir völlig zufrieden: In unserem Dorf der späten Eisenzeit sagt das Modell die relevanten Beobachtungen perfekt voraus (bis zur Erfindung der Atomuhr, 2500 Jahre später; klammern wir das mal aus...). Sollten wir daher an all die frivolen Details der Eifersüchtelein zwischen Clans metaphysischer Kreaturen glauben? Und wenn nicht, warum nicht?
An der Stelle wird die Frage interessant: Ohne Zugang zu den Sphären über den Wolken (nehmen wir an, wir befinden uns immer noch 2500 Jahre vor unserer Zeit) kann man nicht direkt überprüfen, ob all diese Details der Geschichte stimmen. Trotzdem hätten wir (damals schon) stutzig werden müssen. Das Problem ist, daß die Geschichte unnötig kompliziert ist. Man kann viele Details ändern, ohne daß sich die Voraussagen ändern (streiten sich die Göttern von Tag und Nacht über politischen Einfluß, Liebesaffären, oder schlicht über die Vorliebe für schwarz mit weißen Punkten vs. Blau mit weißen Flecken?). Anders gesagt: Das Modell funktioniert zwar gut in Bezug auf die Voraussage in der konkreten Situation, aber weitere Informationen sind redundant; wie genau die Götter heißen, und worüber sie sich streiten ist nicht an Fakten irgendeiner Art gekoppelt. Das ist ein Problem, da wir Schlüsse über den Schlamassel im Reich himmlischer Aristokraten machen, die wohl völlig unrealistisch sind. Was noch schlimmer ist, ist daß das Model nicht generalisiert: Nehmen wir an, unsere Mythologie entstand im Mainz des frühen fünften Jahrhunderts BC. Würde ein Anhänger dieser Theorie nun eine Reise über die Alpen nach Süditalien antreten, würde er oder sie schnell feststellen, daß die Theorie nicht mehr funktioniert; da der Mechanismus sagt falsche Tageslängen über die Jahreszeiten voraus. Auch ist es nicht einfach, das Modell neu zu kalibrieren. Wenn man einige Wochen im Sommer in Italien verbring, liefert uns die Geschichte mit dem Götterzwist keinen Anhaltspunkt darüber, wie lang die Tage im Winter sein werden.
Vergleichen wir das mit der modernen Version: Die Erde kreist um \(23,4^\circ\) geneigt um die Sonne und dreht sich um die geneigte Achse. Mit wenigen Beobachtungen können wir präzise Jahreszeiten auf dem ganzen Planeten voraussagen. Außerdem ist die Geschichte viel einfacher (Schade eigentlich; der Kampf der Titanen war wesentlich unterhaltsamer). Am meisten hilft hier natürlich, daß das Modell stimmt. Wenn aber die technischen Grundlagen fehlen, um dies zu überprüfen, ist dennoch die Kompaktheit des Models (bei gleichermaßen hoher Präzison) ein Vorteil. Hätte unser Uhrzeitvölkchen z.B. einfach ein paar einfache Polynomfunktionen geringen Grades an die Beobachtungen "gefitted" (an die Beobachtungen angepaßt), hätte man trotzdem eine bessere Voraussagekraft erwarten können als mit der wilden Verschwörungstheorie aus dem Reich der Götter.

Schlechte Nachrichten für Verschwörungstheorien

Das allgemeine Prinzip dahinter ist als " Occam's Razor " (oder das Sparsamkeitsprinzip von Wilhelm von Ockham, englischer Philosoph und Theologe, 1288 - 1347) bekannt: Unter allen möglichen Modellen, die eine Beobachtung gleich genau erklären, sei ein möglichst einfaches zu bevorzugen. David Deutsch spricht davon, daß das Model "hard to vary" sein soll, also schwer zu verändern ohne Genauigkeit einzubüßen (dies ist der Fall bei der geneigten Erde; ändert man Winkel oder Umdrehungsgeschwindigkeiten, paßt nichts mehr; bei der Soap Opera mit den jähzornigen Göttern sind dagegen der Phantasie keine Grenzen gesetzt; man muß nur am Ende die Zeiten abpassen).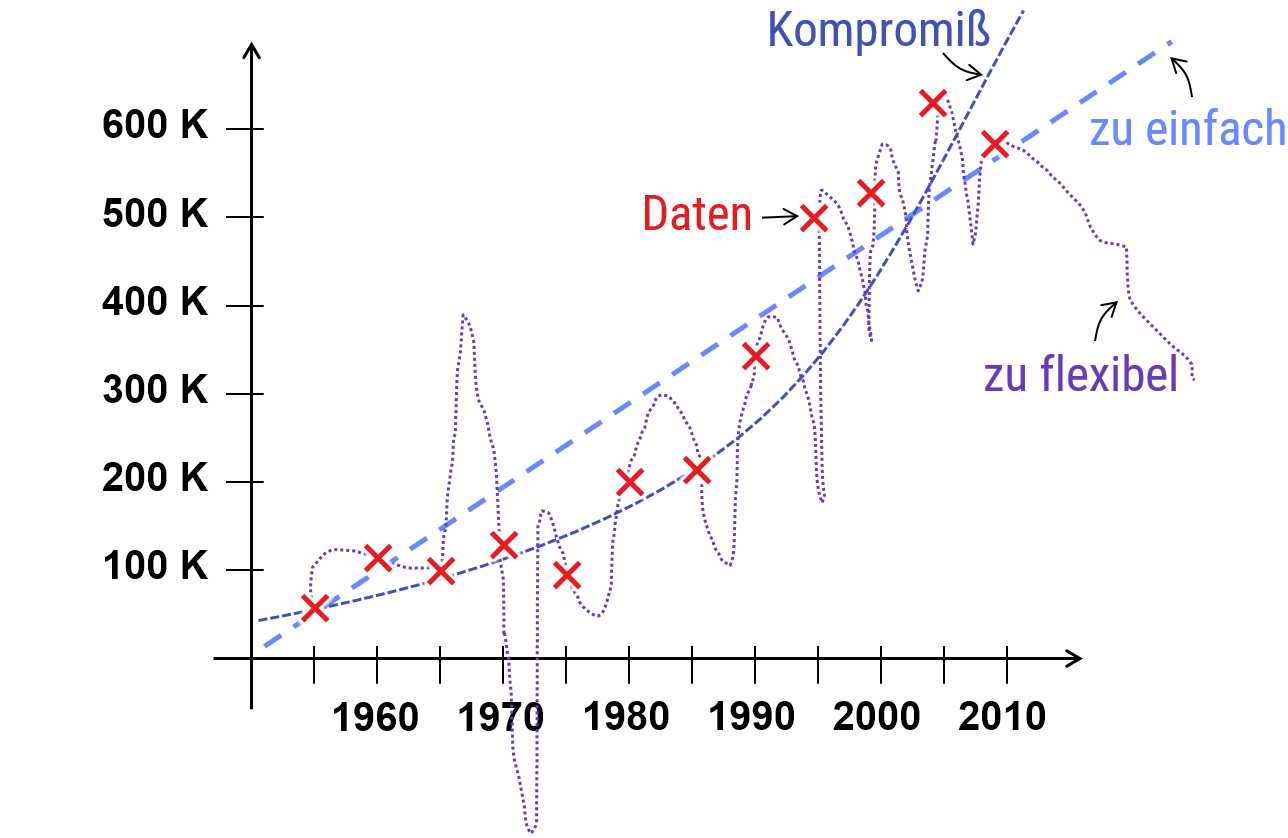

Dieses Sparsamkeintsprinzip - der Versuch komplexe Vorgänge auf möglichst einfache Regeln zu reduzieren, ist ein Grundstein empirischer Modellierung bis heute. Warum es so gut funktioniert, kann man mit Mittel des statistischen Lernens verstehen (im Studium wird dies in den Vorlesungen zum maschinellen Lernen noch im Detail erklärt). Die Grundidee ist, daß jeder zusätzliche "Parameter" des Modells (also Dinge, die wir ändern könnten) durch Beobachtungen abgesichert werden muß. Dazu muß dieser Parameter erstmal überhaupt Einfluß auf das beobachtete Phänomen haben (schwierig bei Zwist von Göttern in Bezug auf Tageszeiten). Zusätzlich sind Beobachtungen ungenau; man muß mehrmals messen, bis das "Rauschen" sich rausmittelt. Hat man viele Schrauben, an denen man drehen muß, so braucht man auch viel mehr Daten, bevor man sich sicher sein kann, daß das Modell stimmt. Hat man diese Daten nicht (oder ein Modell, daß Voraussagen macht, die von Daten unabhängig sind, wie Familienstreit von Götterclans), führt dies zu "Overfitting" (Überanpassung). Das Modell wird instabil und die Geschichte unrealistisch. Auch wenn die (wenigen) Beobachtungen, die wir haben, vielleicht sehr genau erklärt werden, werden neue Situationen in der Regel sehr schlecht vorausgesagt (weil das Modell falsch ist; aber das fällt nicht auf, da man es aufgrund seiner Flexibilität einfach "hinbiegen" kann). Auch nicht direkt beobachtete Aspekte des Modells (Ehestreit im Götterreich vs. Bahnneigung der Erde) ist weniger zuverlässig - auch dies ist eine Variante des Generalisierungsproblems. Die formale Version dieser Zusammenhänge (die mathematische Version von Herrn Occam's Ermahnung zur Einfachheit) ist als im statistischen Lernen als Bias-Variance Trade-off bekannt.

Einige einfache Übungsaufgaben

An dieser Stelle ist es Zeit, daß wir uns über ein paar einfache Aufgaben Gedanken machen. Da in der ersten Woche viel zu lesen ist, halten wir es erstmal eher kurz & einfach:

Mengen

Nach dieser umfangreichen, wissenschaftstheoretischen Vorrede: Werden wir etwas konkreter. Wie sind mathematische Modelle aufgebaut, und wie können wir diese im Rechner umsetzen?

Es gibt viele Möglichkeiten, die Struktur der Mathematik abstrakt auf Grundprinzipien zu reduzieren. Dies kann man, wenn man will, sehr, sehr weit treiben. Der Einfachheit halber beschränken wir uns hier auf ein simples Standardmodell, daß gut zu den Konzepten in der Informatik paßt: Wir bauen alles aus Mengen und Funktionen auf. Schauen wir uns erstmal ersteres an - die Sache mit den Mengen. Mehr zu Funktionen in Kapitel 3.

Mengen in der Mathematik

Eine Menge [engl. set] beschreibt eine Sammlung von mathematischen Objekten, die eindeutig identifiziert werden können. Diese Objekte heißen Elemente der Menge [engl. set elements]. Folgende Annahmen müssen gelten:

• Für jedes denkbare mathematische Objekt wissen wir, ob es in der Menge enthalten ist oder nicht.
• Wir können zweifelsfrei feststellen, ob zwei solche Objekte gleich sind oder nicht.
• Weiterhin ist die Menge so aufgebaut, daß sie gleiche Objekte nur ein einziges mal enthalten kann. Wir zählen nie, wie oft ein gleiche Objekte in einer Menge enthalten sind; Enthaltensein in einer Menge ist immer ein ja/nein Entscheidung (Verallgemeinerungen von Mengen, in denen Elemente mehrmals enthalten sein können, nennt man Multimengen [engl. multiset / bag]).

Mächtigkeit von Mengen

Die Anzahl von Elementen in einer Menge nennt man deren Mächtigkeit [engl. cardinality]. Wenn die Menge eine endliche Anzahl von Elementen hat, ist dies lediglich eine natürliche Zahl, also 0,1,2,.... Wir können aber in der Mathematik ohne Probleme Mengen definieren, die unendlich viele Elemente haben (z.B. die Menge der natürlichen Zahlen [engl. cardinal numbers], selbst, also die Menge \(\{0,1,2,3,...\}\) usw.).

Eine Menge heißt abzählbar [countable set] genau dann, wenn sie man jedem Element eine natürliche Zahl zuordnen kann, die nur dieses eine Element identifiziert. Tatsächlich kann man in der Mathematik nicht abzählbare ("überabzählbare" [uncountable]) Mengen definieren. Beim Programmieren finden wir so etwas nicht; trotzdem spielen überabzählbare Mengen eine entscheidene Rolle in der theoretischen Informatik. Mehr dazu in Kapitel 3.

Informatik: Mengen in Programmiersprachen

Wenn wir in der praktischen Informatik (beim Programmieren) mit Mengen arbeiten, kann das mathematische Konzept in verschiedenen Formen auftauchen. Wir schauen uns nun als erstes an, wie wir Element einer festen Menge kodieren können. Danach schauen wir, wie wir veränderliche Mengen als Datenobjekte kodieren können, oder anders gesagt, die Elemente der Potenzmenge einer Menge kodieren können.

Kodierung von Elementen einer Menge

Nehmen wir als erstes an, daß wir nur eine feste Menge \(\color{red}M\) betrachten. Wir haben uns also explizit oder implizit auf eine bestimmte Menge festgelegt, und deren Inhalt soll im folgenden in keiner Weise geändert werden.

Kodierung von Elementen einer endlicher Mengen

Der Einfachheit nehmen wir zunächst an, daß die Menge endlich viele Elemente hat. Wie können wir die Elemente kodieren? Die einfachste Möglichkeit besteht darin, jedem Element eine natürliche Zahl zuzuordnen und dann einen Bitstring zu speichern, der diese Zahl kodiert.

Sei z.B. \(\color{red}M=\{{\color{functionCol}m}_1,{\color{functionCol}m}_2,{\color{functionCol}m}_3,{\color{functionCol}m}_4,{\color{functionCol}m}_5\}\) eine Menge mit 5 Elementen. Wir können die Elemente nun, unabhängig davon, was diese eigentlich bedeuten sollen, im Speicher repärsentieren, indem wir jedem Element eine Zahl zuordnen. In unserem Beispiel könnten wir zur Darstellung eines Elements der Menge (mindestens) drei Bits reservieren, und dann die fünf Elemente durch die folgenden Zahlen mit Ihren Binärcodes darstellen: \({\color{red}m}_1\equiv 0\equiv\)000, \({\color{functionCol}m}_2\equiv 1\equiv\)001, \({\color{functionCol}m}_3\equiv 2\equiv\)010, \({\color{functionCol}m}_4\equiv 3\equiv\)011 und \({\color{functionCol}m}_5\equiv 4\equiv\)100. Welche Zahl wir für welches Element verwenden, ist dabei völlig egal - wir können das irgendwie festlegen, müssen dann aber immer konsistent bleiben. Das unser Speicherplatz Elemente dieser speziellen Menge enthalten soll (und daher, in unserem Beispiel, auch mindestens drei Bit groß sein muß; weitere würden einfach ignoriert) müssen wir anderweitig sicherstellen (implizit im Program kodiert, indem im Programablauf sichergestellt wird, daß der Speicherplatz nur dafür genutzt wird). Auch kann es ungültige Codes geben (in unserem Beispiel die Binärzahlen für \(5\equiv\)101, \(6\equiv\)110 und \(7\equiv\)111. Wenn wir mit 8 Bits rechnen (auf den meisten Computern einfacher zu programmieren), gibt es sogar \(256-5 = 251\) ungültige codes). Auch hier muß unser Programm implizit sicherstellen, daß diese nie benutzt werden (oder zumindest sich mit Exceptions lautstark beschweren, wenn es unbeabsichtigt schief gehen sollte).

Elemente aus einer unendlichen, abzählbaren Menge

Auf einem realenRechner können wir natürlich nicht wirklich eine unendliche Menge darstellen. Ehrlich gesagt nehmen gängige physikalische Modelle an, daß ein endlich großes Stück Weltraum, wie der von unserem aktuellen Ort sichtbare (kausal mit uns verbundene) Teil des Universums, nur endlich viele Zustände annehmen kann. Von daher gibt es nichts "wirklich" unendliches in der "Praxis". Man sollte daher unendliche Mengen nicht als wirklich unendlich groß betrachten, sondern als etwas daß unbeschränkt ist, solange der Rechner mitmacht (wir nehmen an, daß wir sehr viel Speicher haben, und bei Bedarf immer mehr einbauen können). In der Praxis können wir "unendlich große Mengen" als "potentiell beliebig groß (nur durch Speicher beschränkt, nicht durch die Programmlogik)" auffassen.

Wie kodieren wir also eine solche "potentiell" unendliche, aber abzählbare Mengen?

Was wir dazu machen müssen, ist eine potentiell beliebig große Binarzahl codieren (unser Programm muß natürlich auch den Speicher managen und genug Platz im Speicher reservieren/bereithalten; lassen wir das mal bei Seite - das ist nicht schwer). Wir brauchen hier also einen Code, der beliebig viele Binärstellen haben kann. Dazu gibt es verschiedene Lösungen. Eine sehr einfache wäre, Zahlen im Zehnersystem, mit mindestens 4 Bits pro Zahl, zu speichern. Da vier Bits 16 verschiedene Zustände kodieren können, würden wir einfach die Zahlen 11-15 als Endemarkierung nutzen (wenn die gesetzt werden, ist die Zahl am Ende). Übrigens: Python benutzt automatisch beliebig lange Binärzahlen zur Darstellung von ganzen Zahlen! (JAVA oder C++ benötigen hier extra Bibliotheken).

Diese Codierung ist recht einfach zu programmieren, aber relativ verschwenderisch. Eine bessere Möglichkeit sind Huffman-Codes, die gezielt einen Binärstring erzeugen, dem man ansehen kann, wo er aufhört, und versuchen jedes Bit optimal einzusetzen. Noch etwas besser (um Bit-Bruchteile besser und theoretisch fast optimal) sind sogenannte arithmetische Codes.

Überabzählbare Mengen: So etwas gibt es in der praktischen Informatik nicht. Kontinuierliche Mengen, wie z.B. die reelen Zahlen (\(\mathbb{R}\) ist überabzählbar), werden immer durch endliche bzw. abzählbare Mengen approximiert (letztere natürlich wieder in dem Sinne, daß die Repräsentation beliebig in ihrer Größe wachsen darf). Meistens werden hier Fließkommazahlen mit fester Bitlänge eingesetzt. Selten findet man auch Darstellungen mit variabler Länge und beliebiger Genauigkeit; in besonders kritischen Anwendungen kommen manchmal auch Brüche (z.B. in Computeralgebrasystemen wie Maple oder Mathematica) oder "Intervalarithmetik" zum Einsatz.

Es ist eine interessante Frage, ob es wirklich kontinuierliche Strukturen in der realen Welt gibt. Aktuelle quantenphysikalische Modelle nutzen oft zusätzlich zu den diskreten Zuständen von endlichen Räumen kontinuierliche Zeitparameter (aber dies mag aber ein Artefakt dessen sein, daß es noch keine akzeptierte Quantentheorie von Raumzeit gibt). Wir können kontinuierliche Mengen aber problemlos beliebig genau approximieren. Die Frage scheint eher von philosophischem Interesse mit geringer praktischer Auswirkung.

Ein größeres Hindernis sind andere, nicht unbedingt "kontinuierliche" Mengen, die mächtiger als abzählbar sind (wie z.B. die Menge aller korrekten Sätze in einem Axiomensystem, oder die ebenfalls überabzählbare Menge aller Funktionen zwischen zwei abzählbar-undendlichen Mengen.). Das macht uns in der Informatik und in der Mathematik sehr großen Ärger. Mehr dazu weiter unten!

Was sagt uns das? Diese Sache mit der Kodierung von Elementen einer Menge klingt, ehrlich gesagt, reichlich trivial. Wir haben das schon in den Grundvorlesungen gelernt (und wahrscheinlich schon vorher gekannt). Es ist aber dennoch interessant, daß sehr Arten von Daten in der Informatik in der Praxis genau so konstruiert werden. Z.B. werden ganzen Zahlen, wie z.B. 32-Bit unsigned integer in fast allen Programmiersprachen genau über solche Bitcodes repräsentiert. Auch die Menge aller möglichen Programme (als Maschinencodes) ist als potentiell beliebig langer Bitstring codiert. Einige Codes (wie in unserem Beispiel auch) sind dabei ungültig; nur sind die Regeln etwas komplizierter (Syntax der Programmiersprache).

Mengen als Datentypen

Diese Betrachtung führt direkt dahin, daß Datentypen in der Informatik als natürliche Entsprechung einer mathematischen Menge auffassen sollten: Wir bilden eine Menge von möglichen Werten, die eine Variable annehmen kann; diese Menge ist der Typ. Jeder mögliche Wert entspricht genau einem Element dieser Menge. Ungültige Codierungen, denen keine Elemente zugeordnet sind, entsprechen nicht erlaubten Zuständen des Datentyps.

Beispiel: Eine doppelt verkette Liste (jeder Knoten speichert eine 32Bit-Zahl) wäre eine solche Menge. Jede mögliche Liste ist ein Element der, abzählbar unendlichen, Menge aller verketteter Listen. Kodiert wird die Menge durch mehrere Speicherbereiche, die mit Zeigern verbunden sind. Inkonsistente Zeiger (z.B. node.next.prev != node) sind ungültige Codes; sie entsprechen keinem Element der Menge aller (korrekt) doppelt verketteter Listen.

Abstrakte Operationen auf Mengen: Wir haben in unserer Definition von Mengen gesagt, daß es zu einer Menge auch immer Operationen definiert werden müssen. Mindestens muß dies eine Menge erlauben, Elemente auf Gleichheit zu Prüfen. Außerdem muß sie feststellen können, ob ein Objekt Element der Menge ist. Dies paßt hervorragend zu unserem Verständnis von Mengen als Datentypen:

In diesem Sinne muß also jeder Datentyp eine Vergleichsoperation bereitstellen: Für zwei Elemente des Typs muß man in der Lage sein, festzustellen, ob diese Werte gleich sind oder nicht. Außerdem muß es (je nach Programmiersprache implizit oder explizit) möglich sein, zu überprüfen, ob eine Variable von einem bestimmten Typ (Element der Menge) ist.

# Define a new type
class M:
    # more stuff here 
    def __eq__(self, other):
        # compare self and other
        # return true iff equal
        pass
...
# Use the new type
x = M(...)
y = M(...)
if x==y:
    print("the same")

# in this context, set
# membership corresponds
# to type checks
if x is M:
    print("x is of type M")

// Define a new type
class M {
    // ... define data structure ...
    bool equal(M other) {
        // compare this and other
        // return true iff equal
    }
}

...

// Use the new type
M x = new M();
M y = new M();
if (x.equal(y))
    System.out.println("the same");

// check set membership (data type)
if (x instanceof M)
    System.out.println("x is of type M");

// Define a new type
class M {
    // ... define data structure ...
    bool operator==(const M &other) {
        // compare *this and M 
        // return true iff equal
    }
}

...

// Use the new type
M x;
M y;
if (x == y)
    cout << "the same";

// type check - looks great...
if (dynamic_cast<M*>(&x) != 0)
    cout << "x is of type M";

Kodierung von Mengen selbst

Soweit haben wir uns angeschaut, wie wir einzelne Elemente einer festen (endlichen oder abzählbar unendlichen) Menge kodieren können. Nun stellt sich die Frage, wie wir Mengen selbst als Datentypen handhaben können.

Mengen von Mengen

Der Vollständigkeit halber: Manchmal möchten wir Mengen von Mengen bilden. Z.B. stehen Python oder JAVA genau vor der Aufgabe, wenn sie den Typ einer Variable speichern müssen (Typen sind Mengen, ein Programm nutzt verschiedenen Typen, wir haben also eine Menge von Mengen).

Mengen von Mengen von Mengen

Naja, die Idee kann man auch rekursiv anwenden.

Dynamische Mengen

Dieser Fall ist interessanter: Wie repräsentieren wir Mengen, deren Zusammensetzung wir dynamisch ändern können (also Elemente einfügen oder löschen)? Als erstes müssen wir uns dazu klar machen, daß eine Menge mit \(n\) möglichen Elementen sich in \(2^n\) möglichen Zuständen befinden kann. Jedes Element kann in der Menge enthalten sein oder auch nicht. Daß heißt, wir müssen \(2^n\) verschiedene Codes darstellen können.

Die Standardlösung ist naheliegend: Wir nutzen einen Binärcode in dem jedes Bit kodiert, ob ein festes Element in der Menge enthalten ist, oder nicht. Für \(n\) Elemente benötigen wir genau \(2^n\) Bits - besser geht's nicht. Abstrakt gesprochen könnten wir auch sagen, wir betrachten die Menge aller Möglichen Zustände unserer dynamischen Menge und wenden an, was wir gerade zuvor besprochen haben.

Wir können dies auch noch anders beschreiben: Dieser "dynamische" Mengentyp soll in einer Speicherstelle jede mögliche Teilmenge der Basismenge kodieren können. Der Wertebereich ist daher genau die Potenzmenge (siehe nächster Abschnitt), und die hat \(2^n\) Elemente wenn die Basismenge \(n\) Elemente hat. Die nummerieren wir dann einfach durch, wie gehabt.

Konstruktion von Mengen

Wie können wir Mengen konstruieren? Hier gibt es verschiedene Techniken in der Mathematik, die ihre Entsprechungen in der praktischen Informatik haben (oft unter anderem Namen).

Mathematische Operationen zur Konstruktion von Mengen

In der Sprache der Mathematik gibt es eine Vielzahl von Operationen, mit denen Mengen konstruiert werden können. Wir schauen uns hier einige wichtige an:

Neue Mengen erzeugen

• Aufzählung: Am einfachsten ist es, alle Elemente direkt aufzuzählen. Z.B. \(M_{rgb}=\{rot, gruen, blau\}\), \(M_{nums}=\{23, 42, 1337\}\). Das klappt natürlich nur für endliche Mengen.
• Induktion: Wir definieren ein Element, sowie eine Vorschrift aus einem bestehenden ein oder mehrere weitere zu erzeugen. Beispiel: Die Menge \(M_{zweierpot} \subset \mathbb{N}\) enthalte die Zahl 1. Außerdem ist für jede enthaltene Zahl auch diejenige enthalten, die doppelt so groß ist. Wir erhalten: \(M_{zweierpot}=\{1,2,4,8,16,32,...\}\). Dies liefert oft (abzählbar) unendliche Mengen; man kann aber auch endliche Mengen induktiv definieren, wenn man Abbruchbedingungen formuliert. Beliebt ist auch die "..."-Notation; hier ist gemeint: Man denke sich die Fortsetzung. Da mathematische Texte sich an Menschen wenden, kann man sowas durchaus nutzen (solange es hinreichend klar ist, was gemeint ist). Für den Rechner ist das natürlich weniger geeignet.
• Auswahl: Wir nehmen aus einer bestehenden Menge Elemente heraus, die ein Kriterium erfüllen. Allgemeine Notation: \(M=\{x \in Basis | x \text{ erfuellt Bedingung}\}\) Beispiel: \(M_{gerade}=\{i \in \mathbb{N} | i >5 \text{ und } i \text{ teilbar durch } 2\} = \{6,8,10,12,...\}\)

Bestehende Mengen kombinieren

Auch hierfür gibt es eine Vielzahl von Möglichkeiten.

• Vereinigung: \(A \cup B = \{ x | x \in A \text{ oder } x \in B \}\)
• Schnittmenge: \(A \cap B = \{ x | x \in A \text{ und } x \in B \}\)
• Restmenge: \(A \setminus B = \{ x | x \in A \text{ und } x \notin B \}\)
• Potenzmenge: \(\mathcal{P}(A) = \{ B | B \subseteq A \}\) (die Menge aller Teilmengen).
• Kartesisches Produkt: \(A \times B = \{ (a,b) | a \in A \text{ und } b \in B \}\) (Menge aller Tupel von Werten aus \(A\) und \(B\))

Das kartesische Produkt bildet Vektoren, bei denen im ersten Eintrag ein Element aus der ersten Menge steht und im zweiten ein Eintrag aus der zweiten. Dies kann man natürlich beliebig fortsetzen:

• n-faches kartesisches Produkt (n fest): \(A \times B \times C = \{ (a,b,c) | a \in A \text{ und } b \in B \text{ und } c \in C \}\) ("n-Tupel").
• n-faches kartesisches Produkt (n eine feste Variable): \(\times_{i=1}^n A_i = \{ (a_1,a_2,...,a_n) | a_i \in A_i \text{ fuer alle } i=1...n \}\) ("n-Tupel" oder auch "Vektoren").
• Menge aller n-fachen kartesischen Produkte (bis zu Länge N): \(\bigcup_{i=1}^N \times_{i=1}^n A_i\). \(N\) kann hier auch unendlich groß sein (das wäre die Menge aller Vektoren mit beliebiger Länge).
• Wenn man für die Längen \(n\) bzw. \(N\) (abzählbar-) unendlich einsetzt, spricht man auch von "Folgen". Folgen sind Vektoren mit (abzählbar) undendlich vielen Einträgen.

Konstruktion von Mengen in Programmiersprachen

Soweit die Wiederholung aus den Mathematik Grundvorlesungen. Nun zum interessanteren Teil - wie findet sich dies in Programmiersprachen wieder bzw. wie setzt man dies praktisch um?

Einfache Bitfelder ("dynamische Mengen")

Ein wichtiger, aber einfacher Fall sind dynamische Mengen, kodiert als Folge von Bits. Jedes Bit entspricht einem Element (1=in Menge enthalten, 0=nicht enthalten, wie in Kapitel 2.2.2.2 beschrieben).

In diesem Fall können Operationen wie Vereinigung und Schnitt sehr einfach durch bitweise logische Operationen berechnet werden. Für die Vereinigung bildet man z.B. ein bitweises "oder" der Speicherbereiche. In JAVA oder C/C++ geschieht dies einfach via:

    int a = ...; // eine Menge, kodiert als Bitstring (max. 32 Elemente)
    int b = ...; // noch so eine Menge
    int vereinigung = a | b;    // bitweises "oder"
    int schnitt     = a & b;    // bitweises "und"
    int komplement  = !a;       // alle bits umdrehen
    int rest        = a & (!b); // a \ b

In Python sieht das ähnlich aus (der Komplement-Operator ist ein "~" statt einem "!").

Datentypen

Alles das ist gut zu wissen, aber nicht besonders aufregend. Interessanter ist die Konstruktion von komplexeren Datentypen. Auch dies kann man in Beziehung zu mathematischen Konstruktionen stellen.

Algebraische Datentypen: Vor allem in der funktionalen Programmierung ist das Konzetpt von algebraischen Datentypen beliebt. Hier werden neue Typen aus bestehenden Typen durch entweder das kartesische Produkt (Tupel/Vektor-Bildung) oder die Vereinigung (Fallunterscheidung) gebildet. In einer Funktionalen Sprache wie ML oder Haskell könnte man Datentypen wie folgt konstruieren (Pseudeo-Code):

    class A {...};         // some data type
    class B {...};         // some other data type
    class Tupel = A x A;   // Vector of two As
    class ArrayOf3A = A^3; // = A x A X A;
    class AOrB   = A | B;  // A or B
    class ArrayOf3AOrB = (A x A x A) | B;

Die selben Konzepte finden sich auch in üblichen Imperativen Programmiersprachen: Vererbung in JAVA oder C++ bildet Vereinigungstypen:

Vererbung als Vereinigung von Typen

Mathematik

Seien \(A,B,C\) Mengen. Wir bilden \(V = A \cup B \cup C\).

Beispiel in Python

class V:
    pass

class A(V):
    # define type A
    ...

class B(V):
    # define type B
    ...

class C(V):
    # define type C
    ...

# type V kann nun A, B oder C sein

Beispiel in JAVA (C++ sieht ganz ähnlich aus)

abstract class V {};

class A extends V {...};
class B extends V {...};
class C extends V {...};

...
V v1 = new A;
V v2 = new B;
// Variable v kann vom Typ A,B oder C sein

Fairerweise muß man sagen, daß die imperativ objektorientierte Version in JAVA (oder Python) gewisse zusätzliche Features bietet, wie das dynamische Laden neuer Klassen (man kann die Vereinigung zur Laufzeit erweitern). Viele statisch typisierte, funktionale Sprachen erlauben dies nicht, bieten dafür aber mächtigere Typüberprüfungen und Konsistenzgarantien (z.B. wird sichergestellt, daß immer alle Varianten behandelt werden; dies ist nützlich, wenn vererbte Methoden das Problem nicht mehr gut modellieren können und man typ-spezifischen Code beim Zugriff auf einen Vereinigungstyp schreiben muß). Auch erscheint die Syntax in JAVA/C++ eher umständlich. Die mathematische Formulierung (und die Umsetzung in funktionalen Programmiersprachen, die sich eng daran orientiert), ist dagegen elegant und reduktionistisch. Was von beiden cooler ist, ist, wie so manches in der praktischen Informatik, Gegenstand von mitunter heftigem Streit.

Unions: Noch eine Ergänzung: Klassische Sprachen wie Pascal, C und (damit auch) C++ erlauben auch die Definition eines union-Typs. JAVA und Python erlauben dies nicht, da man diese Unions sehr leicht falsch benutzen kann. Unions erlauben einen von mehreren Typen am selben Speicherort zu halten:

class A {...};
class B {...};
class C {...};
enum TypTag {typeA, typeB, typeC};

struct V {
    TypTag whichType; // nicht vergessen - C/C++ unions merken sich
                      // keine Typinformation; man muss dies selbst tun.
    union {  // "union" legt alle drei Datenobjekte
        A a; // auf den selben Speicherbereich. C/C++ erlauben 
        B b; // nun Zugriff ueber alle drei Bezeichner und interpretieren
        C c; // den Inhalt jeweils dem Typ entsprechend (ungeprueft).
    }
};

...

V x;
x.whichType = typeA;
x.a = A(...);  // enthält nun Typ A
x.b.func(...); // funktioniert leider auch; inkonsistent!
printf(x.c);   // Auch hier kein Protest vom Compiler. Ups.
...
// Richtige Verwendung!
switch (x.whichType) {
    case typeA:
        x.a =...; break;
    case typeB:
        x.b =...; break;
    case typeC:
        x.c =...; break;
    default:
        throw Exception("should never happen");
}

In der Sprache Pascal ist übrigens der Typdiscriminator (das whichType-Feld im Beispiel oben) vorgeschrieben. In C/C++ kann man es auch komplett weglassen (viel Glück...). In modernen funktionalen (und hybriden Sprachen) sind hier strenge Kontrollen vorgesehen. Die objektorientierte Version aus JAVA ist auch sicher, wenn man nicht mit dynamischen casts arbeitet. Selbst dann führt JAVA zwangsweise dynamische Typprüfungen (wie in Python) durch; schlimmstenfalls erhält man eine Exception; ein unkontrollierter Absturz ist nicht möglich.

Induktive definierte Mengen

Wie sieht es mit den weiteren mathematischen Werkzeugen aus? Bei den meisten ist die Umsetzung naheliegend, und es gibt verschiedene Optionen. Interessant sind induktive Definitionen. In der Informatik heißt "induktiv" meist "rekursiv". Auch hier bieten funktionale Sprachen Abstraktionen, die nah an den mathematischen Konzepten sind (z.B. lazy-Evaluation von rekursiven Funktionen). Aber auch in imperativen Sprachen wie Python oder JAVA kann man solche Methoden einsetzen.

Ein beliebtes Design-Pattern sind Generator- oder Iterator-Objekte. Wir definieren eine Klasse, die in Ihren Objekten im inneren Zustand einen aktuellen Zustand speichert. Mit Hilfe von Membermethoden können wir nun den Induktionsschritte ausführen. Schauen wir uns das Beispiel der Menge der Zweierpotenzen an:

class ZweierPotenz:
    # Am Anfang auf 1 
    def __init__(self):
        self.zahl = 1

    # nächster möglicher Wert
    # (Induktionsschritt)
    def next(self):
        self.zahl = self.zahl * 2

...
x = ZweierPotenz()

# Aufwendige Art, 8 zu sagen
x.next().next().next()
print(x.zahl)

In funktionalen Sprachen lassen sich solche Mengen besonders elegant über "Lazy-Evaluation" definieren.

Kartesische Produkte: Arrays und Structs/Klassen

Kartesische Produkte sind in imperativen Programmiersprachen schlicht Klassen (structs in C) bzw. Arrays. Schauen wir uns das in JAVA an:

// definiert int x int x double
class A {
    int a1;
    int a2;
    double a3;
};

// definiert int^42 = int x int x ... x int (42-mal)
int[] array1 = new int[42];

// Vereinigung aller int v (int x int) v (int x int x int) v ...
ArrayList<int> array2;

In anderen Sprachen (C, Python, C++, Pascal, etc.) sieht das ähnlich aus. Streng funktionale Sprachen wie Haskal kennen keine Arrays - diese nutzen statt dessen induktiv (rekursiv) definierte Schachtelungen von Vereinigungstypen. In JAVA würde das so aussehen:

// definiert int x int x double
// In einer funktionalen Sprache waere dies etwa:
// RekArrayOfInts = int | (RekArrayOfInts x int);
//
class RekArrayOfInts {
    RekArrayOfInts next;
    int value;
};

RekArrayOfInts a = new RekArrayOfInts();
a.value = 23;
a.next = new RekArrayOfInts();
a.next.value = 42;
a.next.next = null;
//
// Ergebnis waere soetwas:
// (23, (42, *Ende*) )