



Institut für Informatik
Nina Luhmann.
Sommersemester 2025Angewandte Mathematik am Rechner
Übungsblatt 4: Numerische Ableitung und Automatic Differentiation
Letzte Änderung : 10:16 Uhr, 12 March 2025Abgabetermin : 16. Juni 2025, 8 Uhr
Abnahmetermin : 16. Juni 2025
Im Rahmen dieses Aufgabenblattes wollen wir ein einfaches Computeralgebra-System programmieren. Am Ende dieses Übungsblattes wird Ihr Programm in der Lage sein, einen linear als Zeichenkette (String) codierten mathematischen Ausdruck in polnischer Notation (z. B.
+ * 3 x / * 4 y 5 \( = 3x + \frac{4y}{5}\)) in eine Hierarchie von Konstanten, Variablen und Funktionen, wie im obigen Bild zu sehen, zu konvertieren. Mit dieser Darstellung können wir nun Computeralgebra betreiben! Genauer wollen wir automatisch die Ableitung der durch den Ausdruck definierten Funktion bestimmen.
Am Rande
Eine typische Aufgabe eines solchen Systems besteht darin, komplizierte mathematische Ausdrücke (etwa \((x\cdot x\cdot x + y\cdot 3\cdot y ) \cdot 40 + x\cdot(x^2)\)) in normalisiertere Formen (z. B. \(42x^3 + 120y^2\)) zu überführen. Dazu bestimmt man Regeln unter deren Anwendung der Ausdruck gleich bleibt. Diese wendet man dann solange nach einem bestimmten Muster an, bis keine der Regel mehr anwendbar ist.
Dies ist jedoch nicht Gegenstand dieses Übungsblattes. Viel mehr soll uns hier interessieren, wie wir einen solchen Ausdruck im Computer realisieren und welche Anwendung ein solcher Operationsbaum (siehe Bild oben) in der Informatik hat.
Überblick über das Übungsblatt
Aufgabe 1 soll Ihnen verdeutlichen, dass eine Daten-basierte numerische Ableitung ihre Tücken hat.
In Aufgabe 2 definieren und nutzen wir endlich die oben erklärte Darstellung mathematischer Ausdrücke, um mithilfe des Ausdrucks numerisch Abzuleiten, insbesondere, wenn es schwer ist, die gegebene Funktion analytisch abzuleiten - ansonsten kann man ja diese nehmen. Insbesondere soll der Computer uns die Arbeit abnehmen, die Ableitung „von Hand“ analytisch zu bestimmen.
In Aufgabe 3 bauen wir einen sehr einfachen Parser, damit Sie den Operationsbaum aus einem String zusammen bauen können.
In Aufgabe 4 schließlich bauen wir aus diesen Teilen einen interaktiven Funktionsplotter, der von einem beliebigen algebraischen Ausdruck ausgehend den zugehörigen Funktionsgraphen und die Ableitung zeichnet.
Warum der ganze Aufwand?
Die Aufgabe soll dazu dienen, sich nochmal genau klar zu machen, welche Art von Information eigentlich in mathematischen Ausdrücken (und mathematischer Sprache insgesamt) kodiert ist; das hilft auch dabei, wenn man später Algebra auf dem Papier betreibt. Außerdem ist es eine gute Vorbereitung für Inhalte, die später im Studium noch von Interesse sind (Programmiersprachen/Compilerbau, Logik, „Symbolic reasoning“, Computeralgebra, etc.). Auch sollen die Zusammenhänge zwischen Informatik und Mathematik klarer werden: Welche Art von mathematischer Analyse lässt sich leicht automatisieren, und welche Probleme sind algorithmisch schwerer zu behandeln?
Funktionsableitungen am Rechner
Funktionsableitungen sind für die Modellierung physikalischer Zusammenhänge von großer Bedeutung. Da viele Probleme und Berechnungen heutzutage automatisch am Rechner durchgeführt werden, ist es häufig eine wichtige Aufgabe, die Ableitung einer Funktion zu berechnen. Auf dem Papier machen wir das meist, in dem wir für eine durch einen algebraischen Ausdruck gegebene Funktion mit Hilfe bekannter Ableitungsregeln einen algebraischen Ausdruck für die Ableitung berechnen. Um diese Arbeit am Computer durchzuführen gibt es mehrere Methoden, die alle ihre Vor- und Nachteile haben. Wir wollen uns auf diesem Aufgabenblatt einige davon anschauen.Symbolische Ableitung: Das ist die oben angesprochene Methode, wie wir Funktionen auf dem Papier ableiten. Im Falle, dass wir eine „gutartige“ Funktion symbolisch vorliegen haben, können wir dem Rechner alle nötigen Ableitungsregeln beibringen und so die Ableitung bestimmen lassen. Der Vorteil dieser Methode ist, dass wir einen geschlossenen Ausdruck für die Ableitung erhalten, den wir oft mit nur wenig numerischen Schwierigkeiten sehr genau auswerten können. Der Nachteil ist, dass die Funktion manchmal nicht symbolisch vorliegt oder der Ausdruck sehr kompliziert ist.
Kombination symbolischer Ableitung und Interpolation: Für einfache Funktionen, etwa Polynome, können wir Ableitung direkt bestimmen. Wenn wir also eine komplizierte Funktion durch eine einfachere approximieren, wie wir das auf Blatt 2 mit den Wetterdaten auf verschiedene Art und Weisen getan haben, so können wir die Ableitung der Approximation bestimmen und erhalten damit eine Näherung der Ableitung der ursprünglichen Funktion. Der Vorteil dieser Methode ist die einfache Umsetzung und breite Anwendbarkeit. Ein Nachteil ist die durch die Approximation auftretenden Fehler — die berechnete Ableitung kann stark von der „richtigen“ abweichen. Diese Methode werden wir uns in der ersten Aufgabe anschauen.
Numerische Ableitung: Die Idee hier ist, dass die Ableitung mathematisch als Grenzwert eines „Differenzenquotienten“ definiert ist. Das erlaubt es, den Wert einer Ableitung über die Berechung eines Differenzenquotienten zu approximieren. Diese Methode wollen wir ebenfalls in der ersten Aufgabe betrachten. Der Vorteil dieser Herangehensweise ist, dass wir nur in der Lage sein müssen, die Funktionen an bestimmen Stellen auszuwerten. Der Nachteil ist, dass der Differenzenquotient eben nur eine Näherung der „echten“ Ableitung ist, und der berechnete Wert daher deutlich vom richtigen abweichen kann.
Automatische Ableitung: Was tun wir, wenn wir eine Funktion zwar symbolisch vorliegen haben, die aber nicht „gutartig“ ist, also im schlimmsten Fall an vielen Stellen gar keine Ableitung besitzt? Ein Beispiel für eine derartige Funktion wäre die Cantor-Funktion. Diese hat zwar überall (außer an den Sprungstellen) die konstante Ableitung 0, aber ähnliche Funktionen mit komplexeren Ableitungen kann man schnell konstruieren. Um solche Funktionen gut abzuleiten hilft uns die Technik Automatic Differentiation. Dieses Tool können wir dazu verwenden für einen gegebenen Punkt eine Ableitung zu bestimmen, ohne die komplette Funktion zu betrachten. Dies ist Gegenstand der zweiten Aufgabe.
Aufgabe 4.1: Numerische Ableitung
Aufgabe 4.1.1: Newtonscher Differenzenquotient
[15 Punkte]Angenommen wir hätten keine symbolische Darstellung unserer Funktion, sondern über einem gleichmäßigen Gitter gemessene Funktionswerte \[f_1,f_2,\dots f_n, \] wie beispielsweise die Wetterdaten, die sie bereits auf dem Aufgabenblatt 2 verwendet haben. (Ist eine symbolische Darstellung gegeben kann selbstverständlich die Funktion abgetastet (siehe Aufgabenblatt 1) und dann auf den Abgetasteten Werten weitergerechnet werden).
Der Newtonsche Differenzenquotient ist definiert als die Steigung zweier „naher“ Funktionswerte: \[ \frac{f(x+h)-f(x)}{h}. \]
Eine alternative Definition ist die folgende: \[\frac{f(x+h)-f(x-h)}{2h}.\]
Indem wir \(f(x) := f_x\) setzen und \(h\) als ganzzahlige Schrittweite definieren, erhalten wir so eine numerische Schätzung der Ableitung der Funktion \(f\).
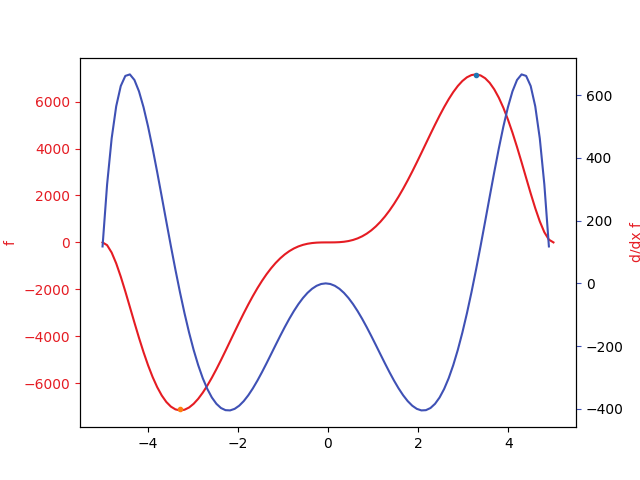



(a) Direkte numerische Ableitung eines Polynoms
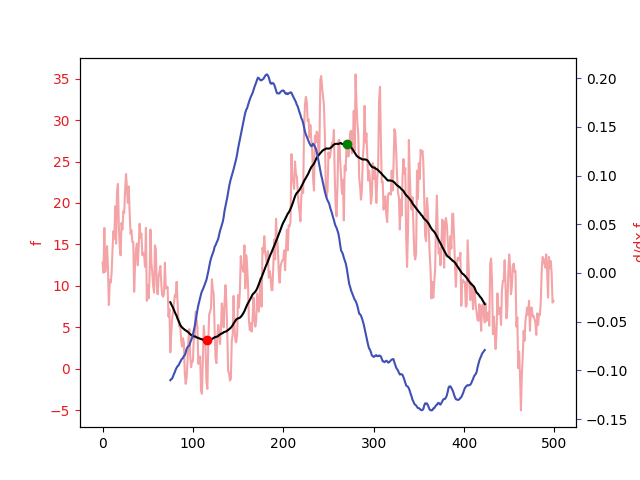



(b) Ableitung eines Wetterdatensatzes mithilfe der Moving-Least-Squares Technik
Numerische Ableitung und automatische Bestimmung von Extremstellen.
Aufgabe
Teil a:- Theoriefrage: Die angegebene Formeln können in dieser Aufgabe direkt auf die gemessen Daten angewendet werden, da diese in einem regelmäßigen Gitter vorliegen. Wie müssten Sie die Formel anwenden, wenn ihre Messung auf einem ungleichmäßigen Gitter erfolgt wäre?
Hinweis: Das heißt Ihre Daten liegen als Punkte-Paare \((f_1,x_1),(f_2,x_2),\dots (f_n,x_n)\) vor.- Starten Sie mit einem beliebigen Polynom und werten Sie es mit
numpyauf einem Gitter aus. - Bestimmen Sie die numerische Ableitung auf dem so entstandenen Datensatz.
- Visualisieren Sie die Ableitung mit Matplotlib. Plotten Sie auch die tatsächliche zugehörige Ableitung, die sie auf dem Papier bestimmt haben (z. B. gestrichelt).
- Testen Sie nun unterschiedliche Schrittweiten \(h\), Gitter und die alternative Definition aus. Was können Sie beobachten?
- Mithilfe der Ableitung können Sie die Maxima und Minima Ihrer Funktion automatisch bestimmen (Suchen Sie nach Vorzeichenwechsel von aufeinanderfolgenden Funktionswerten und achten Sie auf die Art des Vorzeichenwechsels, um die Extrema zu unterscheiden). Visualisieren Sie die Minima und Maxima.
- Optionale Theoriefrage (unbewertet): Im Grenzwert sind die beiden Definitionen für die Ableitung für \(h\rightarrow \infty\) äquivalent. Gilt dies auch für die numerische Verwendung mit endlich kleinem \(h\)?
- Starten Sie mit einem beliebigen Polynom und werten Sie es mit
- Nun zur Praxis:
- Erstellen Sie einen Datensatz, indem Sie \(\sin(x)\) gleichmäßig abtasten und bestimmen Sie dessen numerische Ableitung.
Wie gut approximiert die numerische Ableitung die analytische Ableitung (\(\cos(x)\))?
Zeichnen Sie das numerische, sowie das tatsächliche Ergebnis der Ableitung. - Wie sieht es bei \(\sin(\frac{1}{x})\) aus (beachten Sie, dass diese Funktion an der Stelle \(x=0\) nicht definiert ist)?
- Erstellen Sie einen Datensatz, indem Sie \(\sin(x)\) gleichmäßig abtasten und bestimmen Sie dessen numerische Ableitung.
Teil b:
- Ersetzen Sie nun den Datensatz durch den Wetterdatensatz und Visualisieren Sie auch hier die Extrempunkte in ihrer Darstellung.
- Testen Sie nun unterschiedliche Schrittweiten \(h\), Gitter und die alternative Definition aus. Was können Sie beobachten?
Moral der Geschichte: In der Praxis sind Ableitungen oft mit einem Skalenparameter verknüpft. Die unendlich fein aufgelöste Ableitung macht auf Daten endlicher Genauigkeit keinen Sinn; statt dessen muß an eine (Zeit-/Längen-) Skala angeben (hier durch Wahl des Abstands \(h\)).
Hinweis: Im Verlauf dieses Aufgabenblattes werden Sie immer wieder Funktionen in Abhängigkeit verschiedener Parameter (hier z. B. die Schrittweite) zeichnen müssen. Um verschiedene Parameter gut testen zu können, bietet es sich an, die Funktion in einem interaktiven Fenster mit PyQt darzustellen, in die Parameter in Eingabefelder eingegeben werden können, so dass der Plot automatisch aktualisiert wird, wenn man diese Parameter ändert. Am Ende des Aufgabenblattes sollen Sie einen interaktiven Funktionsplotter erstellen, so dass es vielleicht jetzt bereits eine gute Idee ist, die entsprechenden Vorarbeiten zu leisten und die neu entwickelten Techniken/Plots nach und nach ihrem Funktionsplotter hinzuzufügen.
Aufgabe 4.1.2: Approximative Ableitung
[15 Punkte]Wie sie in Teil b der letzten Aufgabe gesehen haben, ist die direkte Ableitung auf realen Daten problematisch. In dieser Aufgabe geben wir Ihnen einen möglichen Lösungsansatz dafür. Es ist gewissermaßen der Versuch, einen näherungsweisen symbolischen Ausdruck für eine Funktion zu bestimmen, für die wir eigentlich keinen solchen Ausdruck kennen, und dann diesen abzuleiten.
Auf dem Aufgabenblatt 2 haben wir die Wetterdaten durch ein Polynom im Least-Squares-Sinne an den Datensatz „gefittet“. Dies können wir verwenden, um eine approximierte Ableitung des Datensatzes zu erhalten. Dazu muss lediglich eine Polynom in einem Fenster der Breite \(h\) an den Datensatz gefittet werden (Moving-Least-Squares; bisher kein Unterschied zu Ihrer Lösung auf Blatt 2). Danach kann die Ableitung des Polynoms leicht symbolisch bestimmt werden und in der Mitte des Fensters ausgewertet werden. Das Ergebnis ist eine Approximation der Ableitung des Datensatzes im Least-Squares-Sinne.
Aufgabe
- Warum sollte die Ableitung in der Mitte des Fensters ausgewertet werden?
- Bestimmen Sie wie auf Blatt 2 zuerst eine Moving-Least-Squares Approximation. Verwenden Sie dazu ruhig
numpy.polyfit, das ein Array der Koeffizienten des Polynoms als Liste zurückgibt (Koeffizienten zu hohen Potenzen sind in der Liste weiter vorne). - Wie müssen Sie die Liste verändern, damit sie die Ableitung des Polynoms angibt?
Hinweis: Rechnen Sie dies für eine Liste[a_n,...,a_2,a_1,a_0], also für das Polynom \(a_nx^n+\dots + a_2x^2+ a_1x + a_0\), nach. - Die veränderte Liste können Sie, wie die unveränderte auf Blatt 2 auch, in
np.poly1deinsetzen und so als Polynom an einer beliebigen Stelle auswerten. Danach schauen wir uns nochmal die gleichen Anwendungen an (diesmal mit besseren Ableitungen; Tipp: Code modular schreiben...): - Fügen Sie Ihrem Plot das approximierte Polynom und die approximierte Ableitung an.
- Bestimmen Sie auch hier die Minima und Maxima automatisch und färben Sie diese entsprechend ein.
- Bei welchen Fensterbreiten können Sie an den Extrema Tage bzw. Jahreszeiten ablesen?
Aufgabe 4.2: Algebra auf Funktionen
Wie wir in Aufgabe 1 gesehen haben, hat das numerische Ableiten seine Tücken; Schrittweite und „Gutartigkeit“ der Funktion sind direkt dafür verantwortlich, wie groß der Fehler im Vergleich zur echten Ableitung ist. Falls es funktioniert, kann man diese Technik jedoch wunderbar für verschiedene Anwendungen verwenden (siehe nächstes Übungsblatt). Im Allgemeinen ist die numerische Ableitung jedoch instabil.
Die Symbolische Ableitung (die auf diesem Blatt nur am Rande erklärt wurde) kämpft hingegen mit dem Umstand, dass die Ableitung eines Ausdrucks stets wieder einen (einzigen) mathematischen Ausdruck zurückgeben muss. Insbesondere, wenn die abzuleitende Funktion if-Bedingungen und Schleifen aufweist kann dies sehr aufwändig werden. Hier kommt automatisches Differenzieren ins Spiel: Man merkt sich den Operationsbaum eines Ausdrucks und leitet alle Komponenten „direkt“ an der Stelle \(x\) ab, während man beim Abstieg die Kettenregel \[
(f \circ g)'(x) = f'(g(x)) \cdot g'(x)
\] anwendet. Insbesondere bestimmt man also keinen geschlossenen Ausdruck für die Ableitung, sondern führt einfach die Berechnungen an der Stelle \(x\) durch. Die Folge der Operationen, also z. B. welche if-Zweige ausgeführt werden oder wie viele Schleifendurchläufe es gibt, kann dabei für jeden konkreten Wert \(x\) unterschiedlich sein.
Der Nachteil dieser Methode besteht darin, dass man häufig Zwischenergebnisse für die weitere Verwendung abspeichern muss und für jede (elementare) Operation eine Ableitung definieren muss. Außerdem benötigt die Berechnung u.U. mehr Rechenschritte, als die Auswertung des symbolisch bestimmten und ggf. vereinfachten Ausdrucks benötigen würde. Im Gegenzug bekommt man eine Methode, die numerisch sehr viel stabiler ist.
Deep Learning, Hauptmethodik des heutigen nicht-linearen maschinellen Lernens, basiert auf genau solchen Techniken.
Beispielsweise das Framework Tensorflow macht es möglich auf einfache Weise (in Python) einen Berechnungsgraphen zu erstellen, der dann sehr schnell in entsprechende Operationen auf der Grafikkarte (Programmiert in CUDA) übertragen wird. So hat man das Beste aus beiden Welten: Schnelle Berechnung und einfache Bedienung.
Aufgabe 4.2.1: Funktionen-Algebra
[20 Punkte]
Wir starten damit, eine Funktionen-Algebra zu implementieren. Ziel ist es, statt mit Zahlen einfach mit Funktionen zu rechnen, also etwa für zwei Funktionen \(f,g\colon \mathbb{R} \to \mathbb{R}\) soll es möglich sein, \(f + g, f - g, f \cdot g\) auszurechnen. Wir definieren also eine algebraische Struktur auf den Funktionen.
Etwas genauer wollen wir eine sogenannte „Algebra“ \((F, \oplus, \otimes)\) definieren. Die Menge \(F\) ist dabei die Menge aller reellen Funktion \[F = \{ f \mid f \colon \mathbb{R} \to \mathbb{R} \}\] und die beiden Operationen \(\oplus\) und \(\otimes\) definieren eine Addition und eine Multiplikation auf dieser Menge. Wir wollen dabei unter der Summe bzw. dem Produkt zweier Funktionen einfach die punktweise Summe bzw. Produkt der beiden Funktionen verstehen. Das heißt, das Ergebnis der Summe zweier Funktionen \(h = f \oplus g\) ist die Funktion \(h \colon \mathbb{R} \to \mathbb{R}\) mit \(h(x) = f(x) + g(x)\) für alle \(x \in \mathbb{R}\). Genauso verhält es sich mit der Multiplikation und allen anderen Operationen.
Aufgaben
- Erstellen Sie eine Klasse
Function, welche eine Funktionen repräsentiert. Diese Funktion sollte den__call__Operator überladen, der die Funktion an einer bestimmten Stelle auswertet und das Ergebnis zurück gibt.
class Function:
def __call__(self, x):
pass
- Erzeugen Sie nun einige Unterklassen für einige typische Funktionen (
sin,cos,...). Für die Identitätsfunktion könnte das etwa so aussehen:
class Identity(Function):
def __call__(self, x):
return x
- Erweitern Sie die Klasse
Functionnun um die üblichen Operationen+,-,*, /,**. Jede dieser Operationen soll eine neue Funktion zurückgeben, welche die entsprechende punktweise Operation darstellt. Wenn Sie alle weiteren Funktionen als Unterklasse vonFunctionimplementiert haben, dann sollten diese Operationen automatisch auch für alle diese Funktionen funktionieren. Ein möglicher Vorschlag ist der folgende Code-Schnipsel.
Hinweis: Arbeiten Sie am besten mit den von Python zur Verfügung gestellten Methoden__add__,__mul__, etc. wie auch auf dem Aufgabenblatt 3, Mengenaufgabe.
Hinweis: Sie können dabei entweder auflambda-Ausdrücken rechnen oder das Ganze über spezielle UnterklassenAddFunction,SubFunction, ... realisieren. Die zweite Variante benötigt ein wenig mehr Code, ist dafür aber klarer strukturiert und somit einfacher zu verstehen.
Codeschnipsel-Vorschlag
class Function:
...
def __add__(self, g):
return AddFunction(self, g)
class AddFunction(Function):
...
def __init__(self, f, g):
...
def __call__(self, x):
return ...
- Erweitern Sie die
FunctionKlasse um die Kompositionsoperation \((f \circ g)(x) := f(g(x))\) (z. B. als__matmul__Operator, in Python als@geschrieben) implementiert. - Implementieren Sie einige klassische Funktionen als Funktionsobjekte in ihrer Algebra, z. B. die Identitätsfunktion \(id\colon x \mapsto x\), konstante Funktionen \(f_c\colon x \mapsto c\) und \(\sin, \cos, \exp, \ln\).
- (leichter aber freiwilliger) Bonus:
Um auch mit Zahlen zu rechnen, benötigen Sie eine Möglichkeit, konstante Funktionen zu realisieren. Um die Operationen \(f \cdot n\) bzw. \(n \cdot f\) für \(f\colon\mathbb{R}\to\mathbb{R}\) und \(n \in \mathbb{R}\), also Multiplikationen und Additionen mit Zahlen, zu erlauben, müsste man eigentlich immerf * ConstFunction(42)schreiben. Erweitern Sie ihre Operationen so, dass eine Verknüpfung mit einer Zahl ebenfalls unterstützt wird. Ob der übergebene Parameter eine Zahl oder eine Funktion ist, kann man z. B. übertype(x) == Functionoderisinstance(x, Function)testen.
Am Ende dieser Aufgabe sollten Sie in der Lage sein, neue Funktionen durch Kombination (Addition, Multiplikation, ...) zu erzeugen, z. B.
class Sin(Function):
...
f = Sin / Cos + Exp
print(f(42), " == ", math.sin(42) / math.cos(42) + math.exp(42))
- Werten Sie mithilfe Ihrer Methoden einige beispielhafte Funktionen aus visualisieren Sie diese mit matplotlib, z. B. die Funktion \(f\colon x \mapsto \sin(\cos(x) + x^2)\).
(Wir könnten dies nun verwenden, um wie in Aufgabe 1 numerisch Abzuleiten. Die Vorgehensweise sollte an dieser Stelle aber klar sein und muss daher nicht nochmals wiederholt werden.)
4.2.2: Grundprinzip des Automatischen Differenzierens:
[20 Punkte]
Die Idee des automatischen Differenzierens ist die folgende. Wenn wir die Werte einer Funktion \(f\) und einer Funktion \(g\) an der Stelle \(x\) kennen, also \(f(x)\) und \(g(x)\), so kennen wir auch den Wert von \(h = f + g\) an der Stelle \(x\), nämlich \(h(x) = f(x) + g(x)\). Ähnlich verhält es sich mit den Werten der Ableitungen. Kennen wir \(f'(x)\) und \(g'(x)\) dann auch \(h'(x)\), denn es gilt bekanntermaßen \((f + g)' = f' + g'\).
Das funktioniert für + und -, nicht jedoch für *, /, **. Um den Wert der Ableitung \(h'(x)\) von \(h = f \cdot g\) an der Stelle \(x\) zu kennen, reicht es nicht \(f'(x)\) und \(g'(x)\) zu kennen. Warum?
Nun zum eigentlichen Differenzieren:
Statt die Funktion an einigen Stellen auszuwerten und numerisch abzuleiten, schicken wir das ausgewertete Paar \((f(x), f'(x))\) durch den Graphen und definieren alle arithmetischen Operationen auf dem Paar. Wir definieren also eine neue algebraische Struktur \((D, \oplus, \otimes)\) (das sind andere Operationen als für die Funktionenalgebra der vorigen Aufgabe), wobei \[D = \mathbb{R} \times \mathbb{R}\] Paare reeller Zahlen sind. Für zwei Paare \((f(x),f'(x)) \in D\) und \((g(x),g'(x)) \in D\) soll dabei gelten, dass \((f(x),f'(x)) \oplus (g(x),g'(x)) = (f(x) + g(x), f'(x) + g'(x))\) ist, die Addition verläuft also komponentenweise. Für die Multiplikation ist das aber etwas komplizierter und benötigt die Produktregel für die Ableitungen.
Aufgaben
- Setzen Sie dies als neue Klasse um, etwa „DualNumber“. Implementieren Sie für diese Klasse die üblichen arithmetischen Operationen
+,-,*,/und**. (Der Einfachheit halber können sie damit starten zunächst nurf**nfürnganze Zahl zu erlauben)
class DualNumber:
...
def __init__(self, wert, ableitung):
self.wert = wert
self.ableitung = ableitung
def __add__(self, n):
...
...
- Spannend wird das Ganze, wenn wir nun unsere Funktionsklasse
Functionerweitern. Bisher repräsentierte sie eine Funktion \(f\colon \mathbb{R} \to \mathbb{R}\). Jetzt soll sie Funktionen \(f\colon D \to D\) repräsentieren, welche eineDualNumberauf eineDualNumberabbildet. Man übergibt der Funktion also nicht nur den aktuellen Wert, an dem sie ausgewertet wird, sondern auch den Wert der Ableitung und liefert auch beides zurück, den Funktionswert und den Wert der Ableitung. Beachten Sie dabei die Kettenregel \((f(g(x)))' = f'(g(x)) \cdot g'(x)\)
Hinweis: Eine Möglichkeit ist, eine neue KlasseDualFunctionzu implementieren, welche eine Unterklasse vonFunctionist und aus zwei Funktionen, nämlich \(f\) und dessen Ableitung \(f'\) besteht.
class DualNumber:
...
class Sin(DualFunction):
def __call__(self, x):
return DualNumber(math.sin(x.wert), math.cos(x.wert) * x.ableitung)
- Implementieren Sie nun die Elementarfunktionen
sin, cos, tan, exp, ln. - Optional: Implementieren Sie nun \(f^g\) für beliebige Funktionen. Das klappt i.A. nur wenn \(f(x) > 0\).
Hinweis: Nutzen Sie dazu am besten die Gleichung \((f^g)(x) = \exp(g(x)\cdot \ln(f(x)))\) aus.
Testen Sie nun ihr Programm:
- Probieren Sie Ihre Methoden an gewissen Beispielen aus. Ein möglicher Vergleich wäre \(\tan\) und \(\frac{\sin}{\cos}\). (Da sollte das Gleiche herauskommen.)
- Zuletzt vergleichen wir die drei kennengelernte Ansätze, indem wir die Ableitung der Funktion \(\sin(\frac{1}{x})\) aus Aufgabe 1, nun mittels Automatischer Differentiation bestimmen. Fügen Sie das Ergebnis dem Plot aus Aufgabe 1 hinzu und vergleichen Sie die Ergebnisse.
4.2.3 Optionale Aufgabe: Ausgabe des algebraischen Ausdrucks.
Zuletzt, was man mit diesem Berechnungsgraphen noch anstellen kann. Außer reellen Zahlen oder DualNumber kann man eine Funktion auch mit anderen „Werten“ aufrufen und etwas sinnvolles damit machen. Zum Beispiel könnten wir eine „Zahl“ PrintNumber erzeugen, die keinen Wert sondern eine Textdarstellung eines Ausdrucks darstellt. Die einfachste PrintNumber wäre eine Zahl "42" oder eine Variable "X". Mit diesen Zahlen kann man auch Rechnen, dabei wird eine Textdarstellung der entsprechenden Operation erzeugt, z. B. "42" + "X" wird zur Zeichenkette "42 + X".
(Natürlich ist es jetzt nicht mehr so klar, ob \((P, \oplus, \otimes)\) mit \(P\) die Menge der PrintNumber wirklich eine algebraische Struktur im Sinne der Mathematik ist: zwar gibt es Operationen \(\oplus\) und \(\otimes\), aber es ist nicht mehr klar, ob sie den üblichen Axiomen genügen. Zum Beispiel wäre "x" + "5" - "5" dann "x + 5 - 5" und damit nicht wieder "x".)
Aufgaben
- Implementieren Sie die besondere Zahl
PrintNumbermit den üblichen Operationen. Erweitern Sie außerdem ihreFunction-Klassen so, dass sie auch einePrintNumberauswerten können. Das Ergebnis sollte eine Zeichenkette sein, die den Funktionsaufruf repräsentiert, z. B.Sin("42 + X")gibt"sin(42 + X)"zurück. - Optional: Sie können auch den algebraischen Ausdruck der Ableitung mit ausgeben (Natürlich nicht vereinfacht, denn der Ausdruck wird im Allgemeinen sehr wild aussehen). Dazu müssen Sie eine
Dual-PrintNumberverwenden, z. B. in dem die beiden Werte derDualNumbereben vom TypPrintNumberstatt vom Typfloatsind.
Aufgabe 4.3: Parsen — Aus Zeichenketten werden Bäume
[20 Punkte]
Diese Aufgabe enthält relativ viel erläuternden Text. Grund ist, dass wir auch hier wieder etwas neues lernen wollen, nämlich etwas über die Hintergründe von Parsern und kontextfreie Sprachen. Die eigentliche Computeralgebra haben wir bereits in Aufgabe 4.2 implementiert; hier haben wir die Hintergründe schon im Skript und in der Präsenzveranstaltung erarbeitet (daher gibt es dort deutlich weniger Text).
Die letzte Aufgabe beschäftigt sich damit, mathematische Ausdrücke zu manipulieren. Dazu müssen wir diese erstmal in den Rechner bringen. Wie in der Vorlesung erklärt, sind Ausdrücke eigentlich Bäume von Operatoren. Dies ist aber relativ schwierig direkt einzugeben (man bräuchte ein komplexes GUI, und die Interaktion wäre immer noch mühsam, wenn man sich nicht eine sehr raffinierte Schnittstelle überlegt). Daher ist es sinnvoll, mathematische Ausdrücke zunächst in linearisierter Form, als einfache Zeichenketten zu repräsentieren. Die Aufgaben, aus einer solchen, linearisierten Kodierung wieder einen Baum zu rekonstruieren, ist in der Informatik als „Parsing“ bekannt. Der Formalismus dahinter ist als kontextfreie Grammatiken/Sprachen bekannt: In jeden Operator im Baum kann man beliebig komplexe, zusammengesetzte Unteroperatoren einsetzen (Teilbäume).
Wir werden im Folgenden einen Algorithmus entwickeln, der gegeben ein Ausdruck in Polnischer Notation einen Binärbaum erstellt, der die Syntax der Zeichenkette widerspiegelt. Wenig überraschend ist es, dass bei der Übersetzung von Programmiersprachen ganz ähnliche genau die gleichen Konzepte eine Rolle spielen. (Die herkömmliche Mathematische Notation (infix-Notation) zu definieren erfordert etwas mehr Aufwand; es müssen Operatoren mit Präzedenz (Operatorrangfolge) definiert werden, die durch geschicktes Ablegen und Auflegen auf einen Stack in einen Baum überführt werden. Diese Arbeit sparen wir uns an dieser Stelle durch eine sehr viel einfachere Notation.)
Polnische Notation: Beschreibt einen Ausdruck, bei dem alle Symbole durch Leerzeichen getrennt werden und auf jeden Operator eine dem Operator fest vorgegebene Anzahl an Operanden folgt. So benötigt man keine Klammern und jeder Ausdruck ist eindeutig festgelegt. Beispielsweise entspricht + 3 * 2 / 2 5 entspricht dem Term \(3+2\cdot\frac{2}{5}\).
Negation
Sie können dabei den unären Operator - (Negation) entweder durch
- auslassen (es lässt sich ja auch durch
0 - .ausdrücken) - als Teil der Zahl sehen (einfacher)
- ein weiteres Symbol (etwa ~) als unären Operator definieren (Als Beispiel
* ~ 3 / 5 2, dies ist auch nicht viel aufwändiger) realisieren.
Kontextfreie Grammatiken beschreiben die Schachtelung von Bausteinen Fast alle Programmiersprachen benutzen kontextfreie Grammatiken. Das heißt, dass das Programm aus Bausteinen besteht. Jeder Baustein ist ein Platzhalter: Er besteht aus einem gewissen Anteil an festem Text sowie weiteren Platzhaltern (wie ein Baum von Objekten in einer OOP-Sprache: Zeiger auf Unterobjekte müssen einen bestimmten Typ (Oberklasse) haben; welche Teilbäume man einsetzt ist aber egal, solange der Typ des direkt eingesetzten Typen stimmt.).
Die folgende Abbildung zeigt ein Beispiel für eine kontextfreie Grammatik: Die Bausteine sind mit spitzen Klammern markiert und werden mit dem Pfeil-Operator definiert. Auf der rechten Seite steht, mit welcher Folge von weiteren Bausteinen und/oder Zeichen, man einen Baustein ausfüllen kann. Dies macht man, bis alle Lücken (Platzhalter für Bausteine) gefüllt sind:




Eine Kontextfreie Grammatik besteht aus Bausteinen, die Knoten des Baumes entsprechen (hier mit spitzen Klammern und in Farbe markiert). Jeder Baustein kann konkrete Zeichen (grau) oder, hierarchisch geschachtelt, wieder andere Bausteine. Alle Möglichkeiten sind mit Pfeilen aufgelistet; einzelne Varianten mit dem „oder“-Operator (Hochstrich).
Der Parser hat nun die Aufgabe, aus einer gegebenen Zeichenkette (hier sind die Bausteine nicht mehr direkt ersichtlich) zu rekonstruieren, welcher Baum von Bausteinen (also, welche aufeinanderfolgende Ersetzung von Platzhaltern mit rechten Seiten der Pfeile, bis keine Platzhalter für Bausteine mehr übrig sind) zu der Zeichenkette gehört:
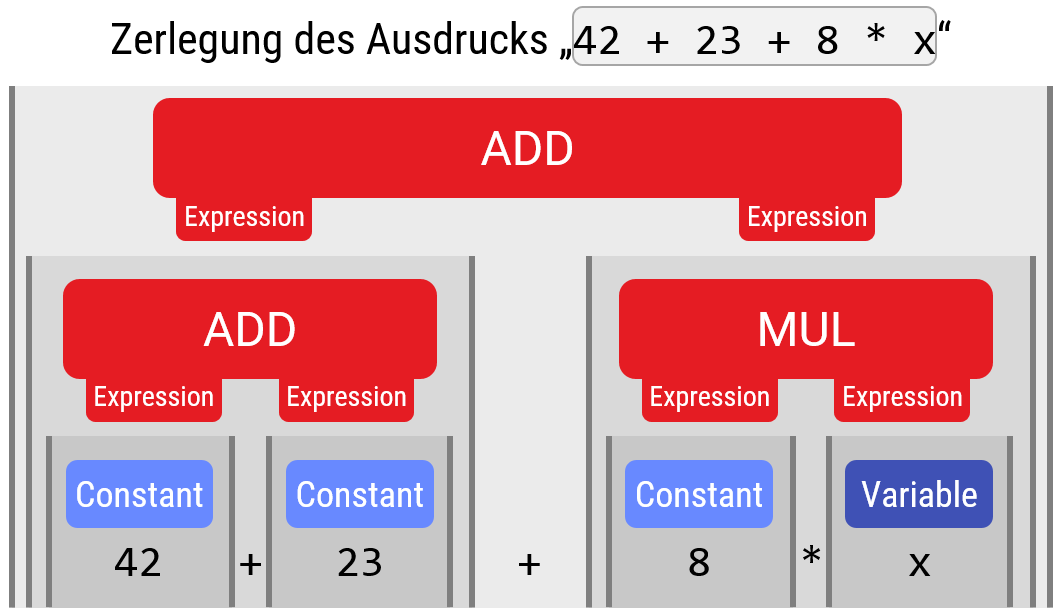



Zerlegung des arithmetischen Ausdrucks \(42+23+8*x\) in Bausteine, die einen Operandenbaum bilden. In dieser Grammatik ist es schwieriger zu erkennen, wo die Grenzen der Bausteine liegen (beim Baustein „Addition“ ist es sogar immer mehrdeutig; die Präzedenz Addition/Multiplikation kann man in der Grammatik einbauen; s.u.).
Leider ist dieses Problem nicht immer einfach. Für unsere Beispielgrammatik gibt es z. B. keine eindeutige Lösung (und das ist ein Problem; die Bedeutung wäre damit nicht mehr klar definiert):
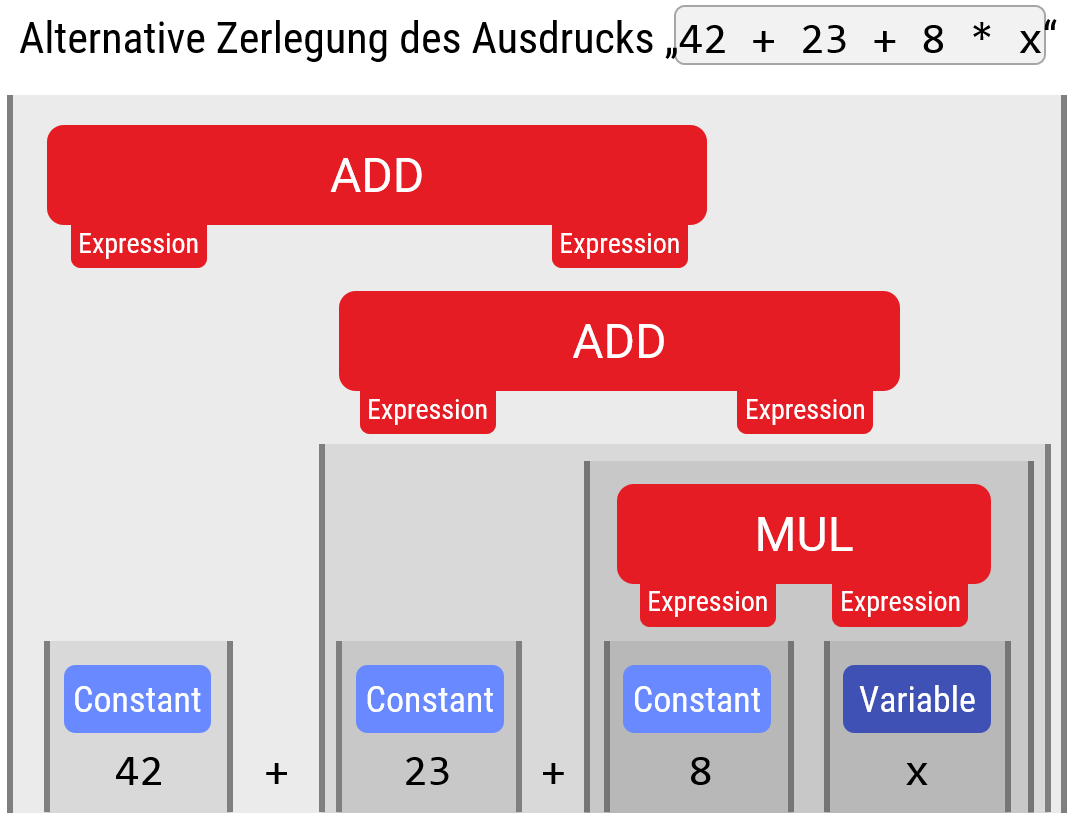



Hier sieht man das Problem: Da keine expliziten Klammern gesetzt wurden, könnten man die beiden Additionsoperationen auch assoziativ vertauschen (was natürlich mathematisch keinen Unterschied macht, und numerisch, bei Fließkommazahlen, nur einen sehr geringfügigen).)
Für das Beispiel mit arithmetischen Ausdrücken, wie hier gezeigt, kann man die Mehrdeutigkeit zwischen Multiplikation und Addition klären, indem man die Regeln geschickter schachtelt. Das Bild unten zeigt die Standardlösung für dieses Problem:




Das Problem, dass Punktrechnung eine höhere Priorität haben soll, läßt sich durch eine Änderung der Grammatik abbilden (der Baustein
MExpr ist spezieller und klammert daher enger). Das Problem der Mehrdeutigkeit beim Plus lässt sich so nicht beheben — hier braucht man eine (nicht-kontextfreie) Sonderregel im Parser.Die gerade beobachte Mehrdeutigkeit bei der Addition löst dies aber nicht; hier muß man im Parser zusätzlich festlegen, dass die Ausdrücke nach links oder rechts geklammert werden sollen (
Man kann es sich natürlich auch einfach machen, und eine Sprache so definieren, dass es sehr einfach wird, die Grenzen der Bausteine und deren Schachtelung zu erkennen. Dazu ist hinreichend, wenn man Anfang und Ende von Blöcken eindeutig markiert, und auch den Typ des Bausteins explizit kennzeichnet. Ein Beispiel für eine solche Sprache ist LISP, in der der Berechnungsgraphen als Klammergebirge kodiert wird, und die Operation immer am Anfang direkt benannt wird:




Die Sprache Lisp vermeidet alle Mehrdeutigkeiten, indem ein vollgeklammterter Ausdruck verwendet wird, bei dem der Name des Operators immer direkt am Anfang jeder Klammer steht, gefolgt von zwei Platzhaltern für Operanden. Ein Parser hierfür ist extrem einfach zu programmieren. Dafür sieht der Code dann etwas unintuitiv aus.
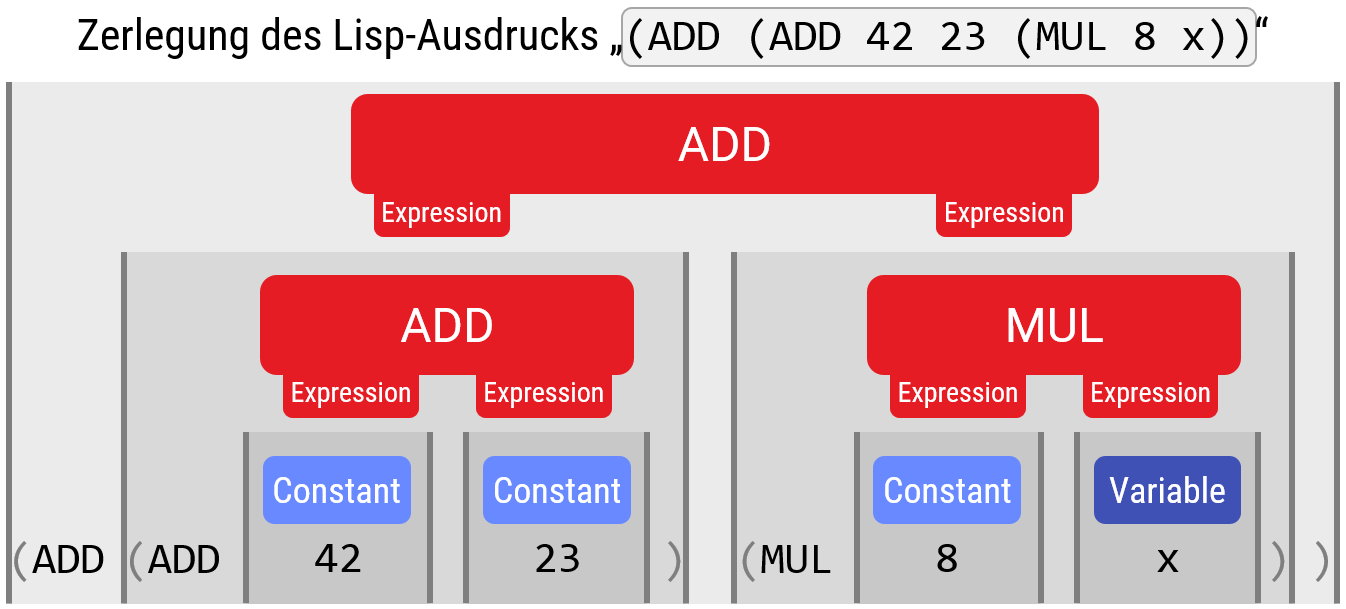



Hier ein Beispiel dafür, wie unser Beispielausdruck in LISP geschrieben würde. Einfach zu parsen — ja, aber nicht unbedingt ästhetisch überzeugend.
Es gibt viele Sprachen, die speziell dafür entworfen wurden, um möglichst einfach zurück in Bäume verwandelt werden zu können. Dazu zählen z. B. XML oder JSON, sowie die meisten Binärformate (auch dies sind oft „kontextfreie“ Schachtelungen von Datenpaketen) von verschiedenen Anwendungsprogrammen, wie z. B. PDF.
Wie funktioniert nun ein Parser?
Die Theorie der kontextfreien formalen Sprachen wird also durch zwei Probleme kompliziert: Zum einen kann es unauflösliche Mehrdeutigkeiten geben, und wir müssen dafür sorgen, dass dies in unserer Codierung keinen Probleme macht. Leider ist dies nicht so einfach zu garantieren. Zum zweiten ist es nicht immer ganz einfach, zu erkennen, wo die Grenzen der Bausteine liegen, auch wenn dies durch die Grammatik eindeutig festgelegt ist. Der einfachste Ansatz wäre ein Backtrackingalgorithmus, der alle Kombinationen, den String in Bausteine aufzuteilen, einfach brute-force durchprobiert, aber das wäre exponentiell (also: viel zu) teuer.
Es gibt Parsingalgorithmen, die jede kontextfreie Sprache (in geeignet transformierter Form der Grammatik) in \(\mathcal{O}(n^3)\) Zeit in einen Baum übersetzt (für \(n\) Eingabezeichen). Das ist zwar nicht unmöglich teuer, aber immer noch sehr praxisfern. In der Praxis nutzt man daher in der Regel spezielle Typen von Grammatiken (LR(0), LR(1), LR(k), LL(k) u.ä.), die den Entwurf der Sprache zu Gunsten der Effizienz etwas einschränken. Dazu gehören dann effiziente Parsingalgorithmen wie der LR-Parser (Bottom-Up-Parser) oder Recursive Descent Parser (Top-Down-Parser). Diese Grammatiken zeichenen sich dadurch aus, dass man nur einige wenige (maximal k) aufeinanderfolgende Symbole anschauen muß, um mit Sicherheit entscheiden zu können, wie der Baum aufgabaut werden muß (eine volle Klammerung wäre z. B. eine LR(0)-Sprache — bei jeder Klammer weiß man sofort, was zu tun ist).
In unserer Aufgabe schauen wir uns eine einfache Sprache für mathematische Ausdrücke an, für die man einen einfachen Parser „direkt“ per Hand bauen kann. Für etwas komplexere Notationen benötigt man Algorithmen, siehe etwa shift-reduce parser für (im allgemeinen) LR(k)-Grammatiken.
Dieser Parser baut immer Teilbäume von links nach rechts auf. Hierzu sollten wir uns nochmal genau Abbildung 2 anschauen: geht man von links nach rechts durch die Zeichenkette, erkennt man nacheinander die Teilbäume „(42)“, dann „((42)+?)“, dann „((42)+(23))“, dann „(((42)+23) + ?)“, und so weiter. Wenn man den Baum so aufbaut, muß man zwei Entscheidungen treffen: (1) Wo ist die Grenze eines Elementes, und (2) Wie wird der Baum geordnet (hier gibt es zwei Möglichkeiten: Soll der Operator linker Teilbaum und der aktuelle Operator der neue Wurzelknoten werden, oder umgekehrt?). Um diese Frage zu beantworten, schaut der Parser immer einen Operator in die Zukunft, und legt noch ungeordnete Teillösungen auf einem Stack ab, um diese später zusammenzusetzen. Die Ordnung wird dabei entweder durch die Grammatikregeln (Schachtelungsordnung) entscheiden oder es wird eine zusätzliche Assoziativitätsregel verwendet (wenn man den Parser von Hand schreibt, wie auf diesem Aufgabenblatt, spielt diese Unterscheidung keine Rolle; wichtig wäre das nur, wenn man einen Parsergenerator schreiben wollte, der aus Grammatiken automatisch einen Parser konstruiert).
Im Prinzip kann man mit diesem Formalismus automatische Übersetzer für beliebige Programmiersprachen schreiben (Parsergeneratoren wie z. B. Lex \& Yacc); für unser Aufgabenblatt geht das natürlich zu weit; die handgeschriebene Lösung ist einfach und braucht im Vergleich nur wenige Zeilen Python oder JAVA Code.
Selbstverständlich existieren bereits sehr spezielle Parser für mathematische Ausdrücke; in dieser Aufgabe sollen jedoch Sie die Zügel in die Hand nehmen und — natürlich angeleitet — einen eigenen Parser entwickeln, der die Syntax einer Zeichenkette so in Teile zerteilt, dass die übriggebliebenen Stücke semantisch leicht in Beziehung gebracht werden können.
Aufgaben
- Implementieren Sie nun den Parser
Die praktische Aufgabe besteht nun darin für eine eingegebene Zeichenkette einen dazu passenden Baum auszugeben. Falls Sie, wie vorgeschlagen, für die einzelnen Operationen auf der Funktionenalgebra eigene Unterklassen erstellt haben, ist dies sehr einfach: Sie haben die nötigen Datenstrukturen nämlich bereits! Die Knoten des Baumes sind geradeFunctionObjekte, die Kinder sind jeweils die Operanten der Funktion. Haben Sie etwa eine+Operation erkannt und die beiden Operantenxundyschon geparst, so erzeugen Sie den neuen+Knoten im Baum einfach mitAddFunction(x,y)(die neu erstellteAddFunctionInstanz ist der neue Knoten mit den beiden Kindernxundy). Ihr Parser liest also eine Zeichenkette ein und wandelt sie in ein (verschachteltes)FunctionObjekt um.
Wir betrachten als erstes eine noch weiter vereinfachte Form der Polnischen Notation. Erlaubt sind die binären Operatoren+,-,*,/, sowie Zahlen und Symbole bestehend aus genau einem einzelnen Symbol (0,1,...,9,x,a). Wenn jedes Symbol aus genau einem Symbol besteht, können wir auch die Leerzeichen entfernen. Erlaubt sind zunächst also z. B.:+1+23oder+*+1x3-47.
Gehen Sie also Zeichen für Zeichen durch die eingegebene Zeichenkette und geben Sie den passenden Baum aus. - Lexikographische Analyse:
Im ersten Aufgabenteil haben wir nur mit Symbolen gearbeitet, die nur aus einem einzigen Zeichen bestehen. In der Implementierung möchten wir auch längere Zahlen sowie Funktions- und Operatornamen wiesinodermoderlauben, die aus mehr als nur einem Zeichen bestehen. Daher Teilen wir das Parsen in zwei Schritte auf: die lexikographische Analyse und das Aufbauen des Baumes (auch bekannt als syntaktische Analyse).
Extrahieren Sie dazu beim Parsen zuerst alle im String vorkommenden Tokens in eine Liste. Tokens sind zusammenhängende Folgen von Zeichen, die elementare Sinneinheiten der Sprache bilden: In unserem Fall benötigen wir die folgenden Tokens: Zahlen (die ganze Folge von Ziffern, mit Dezimalpunkt, ist nur noch ein Tokenobjekt), Operatorenzeichen (wie+,*,-), Funktionsnamen (sin,cos) und Variablennamen. Praktischer Weise ist das erkennen der Grenzen eines Tokens in der Polnischen Notation sehr einfach: alle Zeichen, die von Leerzeichen getrennt werden sind eine Sinneinheit bzw. ein Token.
Ein paar Tipps dazu:
Hinweis 1: Gehen Sie zeichenweise durch die Zeichenkette durch und manipulieren Sie den Laufindex entsprechend des Fundes (Python erlaubt Indexmanipulation nicht infor-Schleifen. Verwenden Sie daher einewhile-Schleife).
Hinweis 2: Beginnen Sie damit Leerzeichen abzudecken und dann auch Zahlen beliebiger Länge zu erkennen (weitere Schleife beim Fund einer Ziffer). Eval-Funktionen oder ähnliches sind dabei nicht erlaubt! Speichern Sie Zahlenstrings direkt als Python-Zahlen ab. Verwenden Sie beispielsweise die unten genannten Funktionen, um aus einem String wie etwa „123.34“ eine Python-Zahl zu erstellen oder schnell zu prüfen, ob es sich um eine Ziffer handelt.
Hinweis 3: Da wir auch längere Variablennamen und auch Funktionen und Operatoren erlauben, erstellen Sie eine Gesamtliste aller Tokens, die sie suchen möchten und ordnen Sie die Gesamtliste der Länge nach (längste Tokens zuerst). So können sie die Klasse des aktuell untersuchten Zeichens schneller herausfinden. Später benötigen wir jedoch nicht nur die Token, sondern auch die Referenz auf das tatsächliche Objekt (von TypFunctionoderOperator), das diesen Token enthält, um uns die erneute Suche zu späterer Zeit zu ersparen. Es bietet sich also an eine Liste zu erstellen, die aus Tupeln der Art(obj, i)besteht und nach der Länge der Token (obj.token) sortiert wird. (Tipp: Siehe die Python-Funktionsortedundenumerate). Beginnen Sie nun mit dem längsten Token und prüfen Sie, ob dieses an der aktuellen Stelle vorhanden ist. - Der eigentliche Parser
Der Parser bekommt eine Liste von Tokens als Eingabe (er muss sich also nicht mehr um alle kleinen Details kümmern). Sie sollten nun eine Liste aller der gültigen Tokens in Ihrem String haben (mit Wiederholungen und in der selben Reihenfolge, wie in der Zeichenkette selbst.
Übersetzen Sie diese Tokenliste nun mithilfe Ihres Algorithmus aus Aufgabenteil 1 in eine Baumstruktur; jeder Eintrag in der Token-Liste kann nun als ein einzelnes Zeichen erachten werden (das macht die Anpassung des Codes relativ einfach ☺).
4.4 Interaktiver Funktionsplotter
[10 Punkte]



Implementieren Sie nun ein Programm, dass aus einem eingegebenen Ausdruck die zugehörige Funktion sowie die Ableitung zeichnet. Alles was Sie dazu benötigen sollten Sie bereits implementiert haben. Nun muss es nur noch zusammengesetzt werden.
Aufgaben
- Implementieren Sie ein PyQt-Programm mit einem Eingabefeld (
QLineEdit), das einen beliebigen String erwartet und den zugehörigen Plot und seine Ableitung anzeigt. Dazu müssen Sie den Ausdruck aus dem Eingabefeld einlesen, mit Hilfe ihres Parsers in einFunctionumwandeln.
Hinweis: Beachten Sie, dass der eingegebene Ausdruck fehlerhaft sein kann, oder vielleicht auch ungültige Operationen durchführt (Division durch Null). Damit Ihr Programm nicht abstürzt, müssen Sie derartige Fehler abfangen und geeignet reagieren (z. B. könnten Sie dann den Wert 0 annehmen, damit der Rest des Funktionsgraphen dennoch korrekt geplottet wird).) Fehler können z. B. mit den folgenden Python-Befehlen abgefangen werden:
try:
... # Code mit evtl. Laufzeitfehlern
except:
... # Behandlung im Falle eines Fehlers
Mögliche Erweiterungen:
- Auswahl zwischen der numerischen und mittels Automatischem-Differenzieren berechneten Ableitung
- Zeichnen Sie auch die Tangente an frei auswählbarem Punkt (um zu sehen, dass die Ableitung auch wirklich die Ableitung ist)
