Institut für Informatik

Nina Luhmann.

Sommersemester 2025

Aufgabe 3.1: Operationen mit endlichen Mengen

Aufgabe 3.1.1: Mengenklasse.

[15 Punkte]

Als erstes definieren wir die Mengenklasse selbst (selbstverständlich ohne die Standardklasse set aus Python zu verwenden!).

• Definieren Sie die Klasse Set (Python unterscheidet Groß- und Kleinschreibung; daher können wir die so nennen). Ihr Konstruktor soll dabei eine Liste von beliebigen Python-Objekten als Argument enthalten, die die (unterschiedlichen!) Elemente der Menge enthalten. Speichern Sie diese Liste intern ab.
• Implementieren Sie die Methode __str__(self), die (grundsätzlich für Python-Objekte) eine Repräsentation als Zeichenkette (String) zu einem Objekt der Klasse ausgeben soll. Verwenden Sie dabei die übliche Mengennotation (z.B. \(\{a,b,c\}\)), wobei die leere Menge durch ein gesondertes Symbol (üblicherweise \(\emptyset\)) gekennzeichnet wird. Durch Sie können Sie ihre Menge einfach ausgeben lassen, wie etwa mit:

  A = Set(["hund","katze","maus"])
  print(A)
  # {hund, katze, maus}
  

• Implementieren Sie nun die Mengenoperationen (ob sie Funktionen oder Operatoren definieren ist ganz Ihnen überlassen)
  • union(A,B) oder alternativ __add__ oder __or__ (Vereinigung \(A \cup B\)),
  • intersect(A,B) oder __and__ (Schnitt \(A\cap B\)),
  • complement(A,B) oder alternativ __sub__ (Komplement \(A\setminus B\)). Achten Sie dabei darauf, dass jedes Element nur einmal in einer Menge enthalten sein darf.
  • Um in späteren Aufgaben bequem Teilmengen aus Mengen zu erstellen, implementieren Sie nun eine Methode subset(self,auswahl), die, basierend auf der aktuellen Mengeninstanz, mithilfe einer gegebenen Auswahlfunktion eine Teilmenge auswählt. In mathematischer Notation würde man hierfür \[\texttt{A.subset(f)} = \{a\in A\, |\, \texttt{auswahl(a) ist wahr}\}\] schreiben.
    
    In Python können Sie die Auswahl bequem durch eine lambda-Funktion realisieren, die für jedes Element der Menge true bzw. false zurückgibt.
    Zwei Möglichkeiten der Verwendung wären

    A = Set(["hund","katze","maus"])
    
    # Lambda-Kalkül: Teilmenge aller Wörter mit vier Buchstaben
    print(A.subset(lambda x: len(x)==4))
    
    # "normal" definierte Funktion: Teilmenge aller Wörter, die ein 'a' enthalten
    def mitA(s):
      return "a" in s
    print(A.subset(mitA))
    

    
    
    
    Nebenbei:

    ---

    Diese Auswahlfunktion wäre damit eine „higher-order function“. Zwar können wir Funktionen als eigenes Konstrukt später noch aus der Menge selbst definieren (siehe herausgestrichene Aufgabe), verstehen den Lambda-Ausdruck an dieser Stelle jedoch nur als sprachliches Konstrukt, das die programmatische Auswahl der Elemente erleichtert und nicht als Funktion).
• Fügen Sie nun weitere Standard Python-Operatoren hinzu, um...
  • ...über die Elemente Ihrer Menge zu iterieren (__iter__(self)),
  • ...zu prüfen, ob ein Element e in Ihrer Menge enthalten ist (__contains__(self,e)),
  • ...die Mächtigkeit Ihrer Menge zu bestimmen (__len__(self))
  • ...und ein Element aus Ihrer Menge explizit abzufragen
    (__getitem__(self,i)).
  Hinweis: Diese Member-Funktionen sind in Python allgemein definiert. Zur Semantik siehe z.B.: https://docs.python.org/3/reference/datamodel.html
  
  Die Methoden erlauben die Handhabung unserer selbstdefinierten Klasse wie im folgenden Code-Schnipsel gezeigt:

  
  A = Set(["hund","katze","maus"])
  
  # subset
  print(A.subset(lambda x: len(x)==4))
  
  # __iter__
  for i in A:
    print(i)
  
  # __contains__
  if "hund" in A:
    print("wau")
  
  # __len__
  print(len(A))
  
  # _getitem_
  print(A[2])
  

Aufgabe 3.1.2: Arbeiten mit der Mengenklasse.

[15 Punkte]

Wir benutzen unsere neue Mengenklasse nun, um einige Anwendungen zu realisieren. Wir beginnen mit einem eher abstrakten Gedankenspiel:

• Definition der natürlichen Zahlen allein aus Mengen: Es gibt eine Konstruktion, mit der man die natürlichen Zahlen mathematisch kodieren kann, ohne dazu Ziffern und Ketten von Ziffern zu benutzen, sondern lediglich geschachtelte Mengen. Ähnlich wie die Peano-Axiome (Wikipedia) definiert auch diese „Von-Neumannsche-Mengendefinition“ die Menge der natürlichen Zahlen \(0,1,2,\dots\) (wir zählen hier die Null dazu; die Konventionen variieren) induktiv wie folgt: \[\begin{aligned} 0 &:= \emptyset\\ 1 &:= \{\emptyset\}\\ 2 &:= \{\emptyset, \{\emptyset\}\}\\ 3 &:= \{\emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}\}\\ &\vdots\\ (n+1) &:= n \cup \{n\} \end{aligned} \] Schreiben Sie eine rekursive Python-Methode, die jede so definierte „Mengen“-Zahl \(n\) ausgibt und testen Sie diese für \(n=15\).
  
  
  Am Rande:

  ---

  Im Grunde könnte der ganze Rest der Aufgabe mit diesem Zahlensystem gelöst werden. Spätestens bei den Funktionen und Relationen, und vor allem bei der Ausgabe ist es jedoch angenehmer, die vorgefertigten Python-Darstellungen der natürlichen Zahlen zu verwenden; lassen wir das also lieber...
  Natürlich dürfen Sie dies jedoch auch mit diesem Zahlenobjekt lösen - was sicher die saubere Alternative wäre.
• Potenzmengen: Nun zu etwas Nützlicherem: einer Methode in unserer Mengenklasse, die die Potenzmenge, also die Menge aller Teilmengen, der aktuellen Menge erstellt. Implementieren Sie diese Methode (powerset(self)). Das Ergebnis dieser Methode sollte dabei selbst auch eine Instanz von Set sein, d.h. die Ausgabe und die restlichen definierten Methoden sollten auch auf der Potenzmenge funktionieren.
  Alternativ können sie auch den **-Operator überladen (__pow__(a,b)).
  Tipp: Binärdarstellung der Mächtigkeit der Menge \(- 1\).
• Binomialkoeffizienten: Das Auswählen von Elementen einer Menge, um damit Teilmengen zu generieren, ist ein kombinatorisches Problem. Es müssen dafür nämlich \(k\) Elemente aus der Menge mit der Mächtigkeit \(n\) gewählt werden. Die Anzahl, auf wieviele Arten man diese Auswahl treffen kann, ist durch den Binomialkoeffizienten \(\binom{n}{k}\) gegeben. Definieren Sie eine Funktion binomialCoefficients(num), die alle Zahlen \(\binom{n}{k}, 0\le k\le n\), ausgibt und verwenden Sie zur Berechnung das Ergebnis der soeben definierte Methode zur Bestimmung der Potenzmenge.
  Anmerkung: Selbstverständlich soll hier nicht die Formel der Binomialkoeffizienten verwendet werden, sondern die zuvor definierte Potenzmenge.

Aufgabe 3.1.3: Kartesisches Produkt

[10 Punkte]

Mengen definieren keine Ordnung ihrer Elemente. Um Anordnungen von Elementen, bei denen jede Position eine andere Semantik hat, zu konstruieren, benötigen wir das Konzept des kartesischen Produktes (Menge aller Paare zweier Mengen):

• Definieren Sie das kartesische Produkt als Unterklasse der Mengenklasse. Dies ermöglicht es Ihnen, mit den neuen Objekten genauso zu arbeiten, wie mit der Basisklasse, insbesondere die Verwendung der vorher definierten Ausgabe und die subset-Funktion.
  Hinweis: Tupel sind bereits fest in Python integriert und dürfen hier verwendet werden (z.B. a = (1,2))
• Fügen Sie der Mengenklasse eine Methode product(self,otherSet) hinzu, um kartesische Produkte bequem erstellen zu können.
  Alternativ können sie auch den *-Operator überladen (__mul__(a,b)).

Aufgabe 3.1.5: (Äquivalenz-)Relationen.

[20 Punkte]

Relationen sind Verallgemeinerungen von Funktionen (bzw. Funktionen sind spezielle Relationen). Eine Funktion ordnet jedem Element einer Definitionsmenge \(A\) ein Element der Wertemenge \(B\) zu. Relationen verallgemeinern dies: Wir können jedem Element aus der Definitionsmenge beliebig viele Elemente der Wertemenge zuordnen (weiterhin kann jedes Element von \(A\) auch vielen verschiedenen Elementen aus \(B\) zugeordnet werden). Anders gesagt: Wir merken uns lediglich für jedes Paar \((a,b), a \in A, b \in B\), ob es in der Relation enthalten ist oder nicht. Relationen sind also Strukturen, die auf dem kartesischen Produkt zweier Mengen agieren (etwa \(A\times B\)).

Wie der Name schon sagt, bringen Sie die Elemente dieser beiden Mengen zu einander in „Relation“:
Die Mengenrelation zwischen den Mengen \(A\) und \(B\) legt für alle Paare \((a,b)\) fest, ob die Elementrelation zwischen Elementen \(a\) und \(b\) entweder besteht oder nicht besteht. Man kann eine Relation also als Teilmenge des kartesischen Produktes definieren, \(R \subseteq A \times B\).
Alternativ kann man dies auch als Funktion \(R: A \times B \rightarrow \{0,1\}\) beschreiben.
Warum ist das so? Erklären Sie dies in der Vorstellung Ihrer Lösung!
(Ganz nebenbei: Durch rekursive Anwendung des kartesischen Produktes, \(A\times (B\times C)\), können auch Relationen auf mehr als zwei Mengen definiert werden; hier schauen wir uns aber nur Relationen zwischen zwei Mengen an.)

Beispiel (einfache Relationen): Sei \(A\) die Menge der in Mainz wohnenden Studenten und \(B\) die Menge der aus Wiesbaden anreisenden Studenten. Wir sagen \(a\in A\) und \(b\in B\) stehen genau dann zu einander in Relation, wenn sie sich kennen.

Axiome für spezielle Typen von Relationen

Relationen helfen uns dabei, komplexere Strukturen zu definieren. Hierzu hat man in der Mathematik Relationen charakterisiert, die in vielen Anwendungen immer wieder auftauchen. Interessant sind dabei oft homogene Relationen \(R\) auf \(A^2 = A\times A\):

Äquivalenzrelation: Ein wichtiges Konzept ist das einer Äquivalenzrelation. Hiermit definieren wir einen vergröberten Gleichheitsoperator „\(=\)“ (auch gerne als „\(\equiv\)“ geschrieben), der die folgenden Eigenschaften erfüllt:

• Reflexivität: Alle Elemente stehen zu sich selbst in Relation.
  Mathematische Definition: \(a \in A \Rightarrow (a,a) \in R\).
  Operatorschreibweise: \(a \equiv a\) für alle \(a \in A\)
• Symmetrie: Steht ein Element zu einem anderen in Relation, dann steht dieses auch zum ersten Element in Relation.
  Mathematische Definition: \(a,b \in A \text{ und } (a,b) \in R \Rightarrow (b,a) \in R\)
  Operatorschreibweise: \(a \equiv b \Rightarrow b \equiv a\) für alle \(a,b \in A\)
• Transitivität: Relationen erlauben den Kettenschluss, d.h. von der Relation zweier Elemente mit einem dritten Element, kann auf die Relation zwischen den ersten beiden geschlossen werden.
  Mathematische Definition: \(a,b,c \in A \text{ und } (a,b),(b,c) \in R \Rightarrow (a,c) \in R\)
  Operatorschreibweise: \([a \equiv b\) und \(b \equiv c] \Rightarrow [a \equiv c]\) für alle \(a,b,c \in A\)

Erfüllt eine Relation diese drei Eigenschaften spricht man von einer Äquivalenzrelation.
Das besondere dabei ist, dass man alle Elemente der Grundmenge so in Teilmengen aufteilen kann, dass alle Elemente jeweils in Relation zu einander stehen, jedoch nicht zu den Elementen der anderen Mengen. Diese Mengen nennen wir (Äquivalenz-)Klassen.
Da die Äquivalenzrelation die Klassenelemente eindeutig zuordnet, stellt man eine Klasse häufig (um Schreibarbeit zu sparen) nur durch einen einzigen (beliebigen, aber eindeutig bestimmten) Repräsentanten dar (siehe Beispiel).
Restklassen werden als Beispiel für Äquivalenzklassen in der nächsten Aufgabe an einem konkreten Beispiel erklärt.

Algorithmische Umsetzung des Findens von Äquivalenzklassen: Programmatisch würde man so vorgehen, dass man mit einem Element startet und es als neue Klasse definiert. Für alle neuen Elemente der Basismenge \(A\) prüft man nun, ob das Element mit dem ersten(!, beliebig aber festen) Element einer der existierenden Klassen in Relation steht. (Warum reicht es aus nur ein Element der Klasse mit dem neuen Element auf Relation zu prüfen?) Falls ja, fügt man das Element der Klasse an, falls es keine passende Klasse gibt, bildet das Element eine neue Klasse.

Ordnungsrelationen auf Mengen (Verallgemeinerung von \(\le\)): Die natürlichen Zahlen sind geordnet, d.h. zu jedem Paar von Zahlen kann man sagen welche Zahl größer (oder gleich) ist. Ordnungsrelationen sind eine (abstrakte) Klasse von Relationen, die einer (bislang ungeordneten) Menge \(A\) eine Reihenfolge gibt. Eine abstrakte Ordnungsrelation muss immer folgende Eigenschaften erfüllen:

• Reflexivität: Alle Elemente stehen zu sich selbst in Relation. \[a \le a \text{ für alle }a \in A\]
• Antisymmetrie: Nur gleiche Objekte stehen in beiden möglichen Reihenfolgen in Relation. \[[a \le b \text{ und } b \le a ] \Rightarrow a = b\text{ für alle }a,b \in A\]
• Transitivität: Auch Ordnungsrelationen erlauben den Kettenschluss, d.h. von der Relation zweier Elemente mit einem dritten Element, kann auf die Relation zwischen den ersten beiden geschlossen werden. \[[a \le b\text{ und }b \le c] \Rightarrow [a \le c]\text{ für alle }a,b,c \in A\]
• Totalität: Eine vollständig geordnete Menge (wie z.B. die der natürlichen Zahlen) legt immer eindeutig fest, welches von zwei verschiedenen Elementen das größere ist: \[a \le b\text{ oder }b \le a\text{ gilt für alle }a,b,c \in A\]
  
  
  Ganz nebenbei

  ---

  Wenn man auf dieses Axiom verzichtet, erhält man eine partielle Ordnung. Zum Beispiel ist die Teilmengenbeziehung „\(\subseteq\)“ eine partielle Ordnung auf der Potenzmenge der Grundmenge: es gilt \(\{red,green\} \subseteq \{red,green,blue\}\) aber es gilt weder \(\{red\} \subseteq \{green,blue\}\) noch das umgekehrte \(\{green,blue\} \subseteq \{red\}\). Anders gesagt: der Beziehungsgraph einer totalen Ordnung ist eine lineare Kette; der Beziehungsgraph einer partiellen Ordnung ist ein azyklisch gerichteter Graph.

Beispiel Beziehungen: Auf der Menge der Personen \(\{\text{Alice},\text{Bob},\text{Charles},\text{Denise}, \text{Eric}\}\) definieren wir eine Relation: X mag Y. (Überlegen Sie sich an dieser Stelle, wer wen mag).

Beispiel Ordnungen: Sei \(N\) eine Menge von Zahlen. Wir definieren die Relation durch \((a,b) \in R_1 \Leftrightarrow a\le b\). Für dieselbe Menge definieren wir zwei weitere Relationen durch \((a,b) \in R_2 \Leftrightarrow a < b\) und \((a,b) \in R_3 \Leftrightarrow a = b\).

Beispiel Restklassen: Sei \(N\) eine Menge von Zahlen und \(m \in N\) eine Zahl (z.B. 5). Wir definieren die Relation durch \((a,b) \in R_1 \Leftrightarrow a - b \text{ ganzzahlig Teilbar durch } m\). Als Repräsentant \(r\) der Restklasse wählen wir stets die kleinste Zahl der Klasse und schreiben die Klasse dann als \([r]\).

Fragen / Aufgaben:

• Wieso teilt eine Äquivalenzrelation auf einer Menge die Menge in disjunkte Klassen ein? Warum reicht es bei dem oben genannten Algorithmus aus jeweils nur die Relation mit einem einzigen Element jeder Klasse zu prüfen?
• Implementieren Sie die Relation als Unterklasse des kartesischen Produktes.
• Fügen Sie Methoden an, die das Prüfen auf Reflexivität, Symmetrie und Transitivität für Sie übernehmen können.
• Frage zu Beispiel 1: Wie muss die Tabelle aller Kombinationen der Personen strukturiert sein (in welchen Zellen steht ein „ist in Relation“), damit es sich um eine
  • reflexive,
  • symmetrische oder/und
  • transitive
  Relation handelt?
• Implementieren Sie die oben eingeführten Relationen (z.B. mithilfe der subset-Methode, die das Relations-Objekt von der Set-Klasse erbt) und prüfen Sie diese darauf, ob es sich um Äquivalenzrelationen handelt.
  
  Hinweis: So wie wir die Mengen hier implementiert haben, sind unendliche Mengen aus Speichergründen nicht darstellbar. Definieren Sie die natürlichen Zahlen als die Menge der ersten 100 positiven ganzen Zahlen..
• Implementieren Sie einen Algorithmus zum Finden der Äquivalenzklassen. Diese kann jedoch nur auf die Relationen angewandt werden, die Äquivalenzrelationen sind. (Geben Sie also im Falle einer falschen Verwendung eine Fehlermeldung zurück).

• Untersuchen Sie die jeweiligen Äquivalenzklassen der implementierten Relationen. Wie zeichnen Sie sich aus und warum?

Aufgabe 3.1.6: Restklassenring

[10 Punkte]

Nun können wir uns endlich dem widmen, was wir zu Beginn versprochen haben — der Implementierung der Kongruenzrechnung, basierend auf der von uns implementierten Arithmetik.

Nun zur eigentlichen Aufgabe:

• Wir schauen uns noch einmal die Relation an, die wir soeben erklärt haben und die Sie bereits implementiert haben (Beispiel 3). Konkret benötigen wir die Restklassen dieser Äquivalenzrelation. Implementieren Sie dazu eine Methode, die ihnen die Menge der Restklassen liefert und eine Methode, die für ein gegebenes Element die Restklasse bestimmt, die dieses Element enthält.
• Auf diesen Restklassen können wir nun eine Arithmetik definieren. Wir definieren wie im Ausblick \([a] \pm [b] := [a\pm b]\) und \([a] \cdot [b] := [a\cdot b]\). Das Ergebnis der Operation ist also stets selbst eine Äquivalenzklasse. Implementieren sie zwei Methoden add und mult, welche die Summe bzw. das Produkt zweier Äquivalenzklassen im Sinne dieser Arithmetik bestimmen.
  
  Wählen Sie als Repräsentanten jeweils das kleinste, nicht-negative Element einer Äquivalenzklasse, damit sie stets Elemente erhalten, die in unserer endlichen natürlichen Menge enthalten sind.

Hinweis: Um besser mit den Äquivalenzklassen arbeiten zu können, empfehlen wir Ihnen eine neue Klasse zu erstellen (z.B. EquivalenceClass), die von Set erbt und lediglich die __str__-Methode überschreibt, um nur einen Repräsentanten auszugeben statt der ganzen Menge.
Sofern Sie möchten können sie auch eine statische Variable einführen, die die Ausgabe steuert, um bei Bedarf doch alle Elemente zu inspizieren.

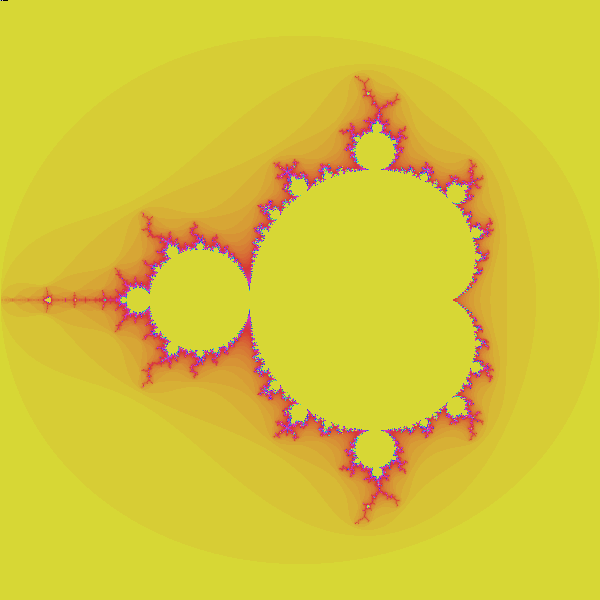
Aufgabe 3.2: Die Mandelbrotmenge („Apfelmännchen“)

Abbildung 3.1: Verschiedene Zoom-Stufen des „Apfelmännchens“. (In den beiden Reihen sind jeweils andere Colorschemes in Verwendung.)

In dieser Aufgabe wollen wir das berühmte „Apfelmännchen“ implementieren.
Dies ist ein Beispiel dafür, wie mit wenigen, sehr einfachen arithmetischen Operationen eine sehr vielfältige und komplexe Struktur entstehen kann. Man nennt dieses Phänomen im Allgemeinen Fall emergente Komplexität — es ist nicht nötig besonders komplexe Regeln zu definieren, um mit diesen sehr komplexe Resultate zu erhalten. Die Turing-mächtige Maschine ist der Extremfall — sie ist universell und kann, mit einem geeigneten Programm, alles erzeugen.
Mandelbrotmengen sind keine Turing-Maschinen; dennoch entsteht eine sehr interessante Struktur aus einer harmlos und simpel erscheinenden Rechenvorschrift.

Wiederholung der komplexen Zahlen:

Bevor wir uns der Mandelbrotmenge selbst widmen, sollen an dieser Stelle nochmals die komplexen Zahlen wiederholt werden.

Die komplexen Zahlen sind die Menge \[\mathbb{C} := \mathbb{R} + i\cdot \mathbb{R} := \{a+ib \,|\, a,b\in \mathbb{R}\},\] die mit der folgenden Struktur versehen sind: Eine komplexe Zahl \(z = a+ib\) besteht damit aus zwei reellen Zahlen \(a,b\) und der imaginären Einheit \(i\), die die Eigenschaft \(i^2=-1\) besitzt. Aus dieser Eigenschaft und der herkömmlichen Multiplikation und Addition auf reellen Zahlen folgen die Rechenregeln: \[\begin{aligned} \text{Addition:}\quad &(a+ib)+(c+id) &= \quad &\, (a+c) + i(b+d)\\ \text{Multiplikation:}\quad &(a+ib)\cdot(c+id) &= \quad &\, (ac-bd) + i(bc+ad)\\ \text{Absolutbetrag (entspr. Länge im } \mathbb{R}^2\text{):} \quad &|(a+ib)| &= \quad &\, \sqrt{a^2 + b^2} \end{aligned}\] Komplexe Zahlen sind glücklicherweise bereits fest in Python und Numpy implementiert. Es unterscheidet sich lediglich das Symbol der komplexen Einheit \(i\): Für Python ist diese nämlich durch j gekennzeichnet.

Mandelbrotmenge:

Wir beginnen mit einer beliebigen komplexen Zahl \(c\in \mathbb{C}\) und definieren die Folge

Die Mandelbrotmenge \(M\) ist die Menge, für die der Absolutbetrag dieser Folge nach oben hin beschränkt ist, mathematisch ausgedrückt:

Aufgabe 3.2.1: Die Mandelbrotmenge (aka: das Apfelmännchen).

[30 Punkte]

Nun werden wir die Mandelbrotmenge darstellen.
Wichtig: An dieser Stelle der Hinweis, dass die Berechnung der Darstellung mit reinem Python nur langsam von statten gehen würde.
Daher sind die Aufgaben so formuliert, dass Sie Numpy verwenden sollten, damit die „Interaktion“ noch Sinn macht. Andernfalls macht der Teil mit dem „Zoomen“ wenig Spaß.
Hinweis: Verwenden Sie dennoch eine geringere Auflösung, damit die Berechnungen noch schneller sind.

• Erstellen Sie eine Qt-GUI, das (wie auch bei der Snake-Aufgabe) ein Bild anzeigen kann. Diesmal benötigen wir jedoch die im Skript erklärte Methode zur Verwendung von Numpy-Arrays als Bild-Daten (Siehe Abschnitt 1.4.10.4 im Skript).
• Generieren Sie nun ein Gitter auf den komplexen Zahlen. (Siehe Skript zu 2D-Gitter). Das Mandelbrotmännchen ist besonders gut für \([-2,1]\times [-1,1]\) zu sehen; starten Sie also in diesem Intervall.
• Implementieren Sie die Folge \(z_n\) vektorisiert, verwenden Sie also keine for-Schleifen über die Einträge des Gitters selbst, sondern nur über \(n\).
  
  Ferner werden wir \(n\) nicht bis unendlich laufen lassen können; limitieren Sie also die maximal Anzahl an zu berechnenden Folgenelementen.
  (Eine Größenordnung von \(n=100\) liefert gute Ergebnisse und hat eine relativ kurze Berechnungsdauer.)
  
  Ob die jeweilige Zahl tatsächlich in der Mandelbrotmenge enthalten ist können wir also nicht bestimmen. Was wir jedoch tun können ist zu zählen, wie lange es dauert, bis die Folge die Grenze \(z_n > 2\) überschreitet. Initialisieren Sie also vor der Schleife ein Numpy-Array, das die gleichen Abmessungen hat wie das Gitter selbst und zählen Sie in genau den Einträgen hoch, in denen der Betrag der komplexe Zahl noch nicht über die 2 gekommen ist.
  
  Hinweis: Die Zähloperation kann auch sehr leicht mit Numpy realisiert werden. Schauen Sie sich dazu Abschnitt 1.2.2.4 über Filtern im Skript an.
• Wir wollen nun abhängig davon, wie groß die Zahl geworden ist eine Farbe festlegen. Dies kann auf verschiedene Arten und Weisen gelöst werden.
  Eine leicht implementierbare Möglichkeit verwendet den HSV-Farbraum statt des RGB-Farbraumes. Dieses wird nicht über die Stärke der Farben Rot, Grün, Blau definiert, sondern über die Farbe, die Sättigung und die Helligkeit, jeweils im Wertebereich \([0,1]\). Einfacher ist die Verwendung von Matplotlib, das bereits eine Auswahl verschiedener Farbübergänge liefert. Keine Panik: Wie dies in Python implementiert werden kann geben wir Ihnen allerdings vor (siehe unten).

• Fügen Sie nun Maus-Interaktion hinzu, indem Sie den Nutzer die Möglichkeit geben, hinein- und hinauszuzoomen.
  Sie können dazu beispielsweise das MousePressEvent verwenden. (Siehe Skript: e.X(),e.Y() liefert Ihnen die Koordinaten in Ihrem selbstdefinierten Gitter.
  • Achten Sie bei der Anzeige (und vor allem beim Zoomen) darauf, dass die x-Achse und die y-Achse gleich skaliert sind, da sonst das Ergebnis verzerrt aussieht.
• Nun untersuchen wir das Ganze:
  • Was passiert, wenn Sie die Anzahl der Schleifendurchläufe erhöhen / senken?
  • Was passiert, wenn Sie die Schranke 2 verändern?
  • Optional, jedoch sehr interessant und mit wenig Aufwand verbunden:
    Die Mandelbrotmenge kann man als Spezialfall einer Funktion ansehen, die die Struktur der Folge ausgehend von einer komplexen Zahl auswertet.
    
    Diese allgemeinere Vorstellung führt zur Julia-Menge. Mit sehr wenig Aufwand können Sie nun andere ähnliche Strukturen wie die Mandelbrotmenge erstellen, indem Sie Ihr Gitter nicht für \(c\) einsetzen sondern für \(z_0\) und für \(c\) eine beliebige andere (feste) komplexe Zahl im Radius \(|c|\le 2\) wählen.
    Die Folge lautet dann \[\begin{aligned} z_0 &\text{ beliebig}, c \text{ fest für alle } z_0\\ z_{n+1} &= z_n^2 + c, \quad \text{ für } n\ge 0. \end{aligned} \] Testen Sie dies aus und achten Sie insbesondere darauf, wie sich die Mengen ändern, abhängig davon ob die Zahl \(c\) selbst in der ursprünglichen Mandelbrotmenge liegt oder nicht.
    Sie können aber auch das interaktiv gestalten: Erstellen Sie hierfür ein zweites Fenster, das die Mandelbrotmenge in Gänze zeigt. Per Mausklick wählen sie nun das \(c\), sodass ihr Hauptfenster als „Lupe“ auf der Mandelbrotmenge agiert.
    Auf YouTube finden sich dazu schöne Visualisierungen. Zum Beispiel dieses.
• Optional und auch mit wenig Aufwand verbunden: Statt das Polynom \(z^2 + c\) rekursiv auszuwerten, können Sie mithilfe Ihres Codes auch andere Polynome von der Form \(p(z) + c\) Testen, ohne viel an Ihrem Code ändern zu müssen.

Beispielcode: Farbschemata mit Matplotlib

# importieren Sie zu Beginn Ihres Codes das Matplotlib-Paket
import matplotlib.pyplot as plt


# ... in ihrer update- bzw. draw-Methode ...


# Normalisieren von count (Werte zwischen 0 und 1)
max = np.max(count)
min = np.min(count)
if max==0:
  max = 1
count = (count - min) / max

# für große n können die Farbübergänge zu stark sein. Dies kann z.B. mit
# count = count**0.25
# umgewichtet werden

# Farbschema anwenden
# (eine Auswahl finden Sie unter: http://matplotlib.org/users/colormaps.html )
colormap = plt.cm.RdYlBu # z.B. in Ihrer GUI Auswählbar
colfloat = colormap(count)

# Qt erwartet Werte zwischen 0 und 255 für RGB-Bilder
colint = np.asarray(colfloat*255, dtype=np.uint8)

# Konvertieren in ein QImage & Anzeigen
img = QImage(colint.data, self.width, self.height, QImage.Format_RGBA8888)
pixmap = QPixmap.fromImage(img)
self.display.setPixmap(pixmap)