



Institut für Informatik
Nina Luhmann
Sommersemester 2025Mathematische Modellierung am Rechner
Übungsblatt 2: Empirische Modellierung
Letzte Änderung : 10:16 Uhr, 12 March 2025Abgabetermin : 19. Mai 2025, 8 Uhr
Abnahmetermin : 19. Mai 2025



In dieser Praktikumsaufgabe wenden wir uns dem Kernthema unserer Veranstaltung zu — dem Einsatz von Werkzeugen der mathematischen Modellierung am Rechner. In dieser Aufgabe wollen wir uns das Problem anschauen, Modelle (d.h. mathematische Beschreibungung) aus empirisch gemessene Daten abzuleiten. Insbesondere werden wir dabei einige der Risiken der empirischen Modellierung (Induktive Schlüsse, „Lernen“ von Modellen aus begrenzt vielen Messdaten) in der Praxis kennenlernen. Am Schluss steht ein „Cross-Validation“-Experiment, mit dem wir messen, wie gut unsere Modelle geeignet sind, Voraussagen über unbeobachtete Daten zu machen.
Als Beispiel schauen wir uns den Klassiker unter den Vorhersageproblemen an: Die Wettervorhersage. Komplexe Klimamodelle oder etwa die Analyse von Satellitenbildern gehen dabei hier noch über unsere Möglichkeiten hinaus. Daher schauen wir uns eine einfachere Variante dieser Aufgabe an: Wir nehmen historische quantitative Daten (Temperatur, Niederschlag o.ä.) und möchten diese auf (noch) nicht beobachtete Zeitpunkte interpolieren bzw. extrapolieren. Dazu schauen wir uns einen realen Datensatz an: Die Temperatur in Frankfurt am Main der letzten 1,5 Jahren.
Wir wollen uns einige Möglichkeiten anschauen, wie wir eine Kurve an einen Datensatz "fitten" (also anpassen) können. Ziel der ersten Aufgabe ist es, verschiedene einfache Modelle an den Datensatz zu fitten und so ein Gefühl für Modelle im Allgemeinen zu bekommen.
Hinweis zur Gestaltung dieser Aufgaben
Dieses Aufgabenblatt enthält relativ viel Text, um die Verfahren zur Datenvorhersage zu erklären. Davon sollten Sie sich nicht abschrecken lassen — die Lösung der einzelnen Aufgaben erfordert in der Regel nur wenige Zeilen Code. Die Erläuterungen sollten Sie trotzdem sehr sorgfältig lesen und durcharbeiten — hier lernen Sie bereits einige nützliche Techniken für die maschinelle Datenanalyse (dies wird später im Studium noch vertieft). Um die Erklärungen auf diesem Aufgabenblatt vollständig zu verstehen, reicht Schulwissen aus (insbesondere in Bezug auf: Polynome, Ableitungen, Kurvendiskussion).
Hinweise zur Abgabe (Theoriefragen)
Auf diesem Aufgabenblatt sind immer wieder einige kurze Theoriefragen eingestreut. Diese müssen Sie im Abnahmegespräch beantworten (die Antworten fließen in die Bewertung ein). Hierzu wird, vor allem wenn Rechnungen oder formale Herleitungen nötig sind, dringend empfohlen, schriftliche Notizen anzufertigen und zur Abnahme mitzubringen (bewertet wird allerdings in jedem Fall nur das Gespräch; es werden keine schriftlichen Abgaben eingesammelt).
Bewertung
Wie bei jedem Aufgabenblatt können Sie auch hier bis zu 100 Punkte erreichen.
Der Abgabetermin dieses Aufgabenblattes ist der 19. Mai 2025, 8 Uhr.
Der Abnahmetermin dieses Aufgabenblattes ist der 19. Mai 2025.
Aufgabe 1: Wettervorhersage mittels Funktionsextrapolation
Aktualisierung des Skriptes
- In dieser Aufgabe werden wir einen sehr kleinen Teil des Toolkits Matplotlib verwenden.
„Matplotlib ist eine Python-spezifische (gibt es nur für Python) Bibliothek um schnell einfache Graphen und Plots von Daten und Funktionen anzufertigen. Mit Matplotlib können sehr viele verschiedene Arten von Diagrammen erstellt werden - der Einstellbarkeit sind kaum Grenzen gesetzt - für unsere Anwendungen werden wir jedoch nur auf eine kleine Teilmenge der Funktionen zurückgreifen. [...]“ (im Skript weiterlesen)
Wir benötigen lediglich die Funktionen zum Anzeigen von Punkten und Zeichnen von Linien, die im Skript genauer erklärt werden. - Ein weiteres Python-package, das wir Ihnen hier sehr empfehlen ist Numpy.
„Numpy ist ein Python-Paket, das effiziente Operationen mit (großen) Arrays von numerischen Daten unterstützt. Python als Skriptsprache ist sehr langsam. Bei numerischen Operationen, bei denen große Vektoren mit vielen Einträgen bearbeitet werden sollen, fällt dieser Nachteil besonders ins Gewicht. [...]“ (im Skript weiterlesen)
Zwar handelt es sich bei dieser Aufgabe noch nicht um riesigen Datenmengen, in späteren Aufgaben ist der Performanceunterschied viel deutlicher. (Ohne numpy, kann die Ausführung ihres Programmes mehrere Minuten in Anspurch nehmen). Daher empfehlen wir Ihnen sich bereits jetzt mit Numpy auseinanderzusetzen.
Programmstruktur
Für die Gestaltung Ihres Programms gibt es verschiedene Möglichkeiten: Die einfachste ist, Matplotlib direkt zu verwenden und in Ihrem Python-Skript einfach nacheinander verschiedenen Diagramme zu erzeugen und anzuzeigen. Diese erscheinen standardmäßig in eigenen Fenstern, die von Matplotlib selbst erzeugt werden; eine weitergehende Interaktion mit der Anwendung ist dann allerdings nicht möglich (es läuft einfach das programmierte Skript ab).
Falls Sie bevorzugen, eine interaktive Anwendung mit einem frei programmierten GUI zu gestalten (dies ist für diese Aufgabe aber nicht unbedingt nötig) können Sie Matplotlib-Plots auch in einem Qt-Widget anzeigen lassen (siehe Skript für ein Beispiel)..
Daten
Auf der Seite des Deutschen Wetterdienstes können Tagestemperaturen verschiedener Orte in Deutschland heruntergeladen werden (der Download-Button befindet sich unter den Daten selbst, links vom Druck-Symbol). Die Tabelle selbst enthält viele verschiedene Arten von Messwerten; in dieser Aufgabe beschränken wir uns aber auf Temperatur und Niederschlag (jeweils separat, als eindimensionale Funktion der Zeit. Wir müssen hier die entsprechende(n) Spalte(n) auswählen.
Falls die Seite des Deutschen Wetterdienstes nicht funktioniert, können Sie auch diese Testdaten (für München) verwenden
Aufgabe 1.1: Darstellung des Datensatzes.
[10 Punkte]




Nun geht es an die Arbeit. Als erstes schauen wir uns die Rohdaten an. Bearbeiten Sie hierzu die folgenden Teilaufgaben:
- Vorbereitung (optional): Lesen Sie Kapitel 1.3 („Matplotlib“) im Skript.
- Wählen Sie von der Webseite des Deutschen Wetterdienstes einen Standort aus (z.B. „Frankfurt/Main“) und speichern Sie die Tabelle in einer Textdatei ab. (Falls die erste und letzte Zeile öffnende bzw. schließende
pre-HTMLTags, müssen Sie diese erst löschen.) - Lesen Sie mithilfe von Numpy die Tabelle ein (dies ist in Python sehr einfach; siehe Skript zu
np.loadtxt(...)). - Extrahieren Sie die maximale Temperatur in 2m über dem Erdboden (
TX) sowie die Niederschlagsmenge (RR) (siehe im Skript unter „mehrdimensionale Arrays“ zur Extraktion von Spaltenvektoren, z.B. mitspalte = tabelle[:,spaltennummer]).
Als erstes möchten wir den Datensatz selbst in Matplotlib ansehen.
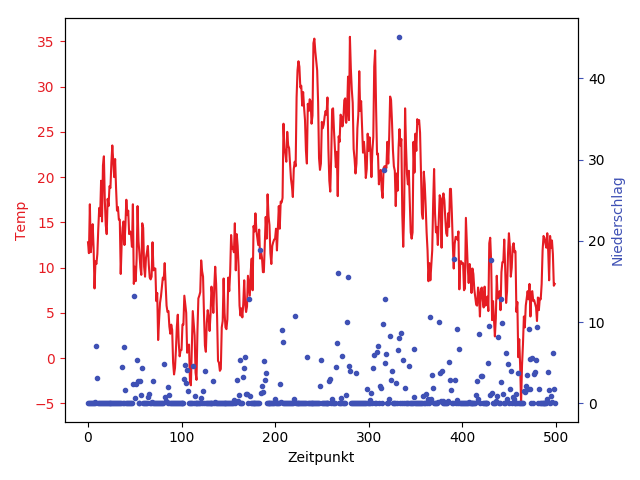
Stellen Sie die die beiden Zeitreihen in Matplotlib dar (siehe Abbildung 1). Verwenden Sie für die x-Achse die Zeilennummern des Datensatzes (siehenp.arange(...)) und definieren Sie zwei y-Achsen für die jeweiligen Spalten, die auf der linken bzw. rechten Seite des Plots angezeigt werden.
Um Verwirrung zu vermeiden:
Stellen Sie die beiden Zeitreihen unterschiedlich dar: entweder mithilfe verschiedener Farben, oder mithilfe verschiedener Symbole für die Punkte selbst. (Fügen Sie auch eine Legende hinzu, an der man die Bedeutung der Visualisierung ablesen kann.) - Verbinden Sie die Punkte durch Linien (siehe Matplotlib-Kapitel im Skript). Dies ist auch schon ein erstes Modell, das gewisse Vorhersagen in den Wetterdaten macht (Frage: in wie fern?).
- Ohne viel an Ihrem Code ändern zu müssen, können Sie auch Teildaten ansehen. Fügen Sie dazu
tabelle = tabelle[startindex:endindex,:]vor die Spaltenextraktion ein. Probieren Sie dies aus. (Wir werden für die anderen Teilaufgaben der Übersichtlichkeit halber nur Teildaten verwenden.) - Was fällt Ihnen dazu auf? Wie gut ist das Modell und wie gut hilft es uns bei der Vorhersage bzw. wie gut approximiert es den Verlauf der Wetterkurve selbst? Denken Sie beispielsweise an Fehler oder Ungenauigkeiten; diskutieren Sie, in wie weit in die aus den Messungen gewonnenen Erkenntnisse verallgemeinert werden könnten (z.B. für den nächsten Tag, die nächste Woche oder das nächste Jahr).
Aufgabe 1.2: Polynominterpolation
[15 Punkte]
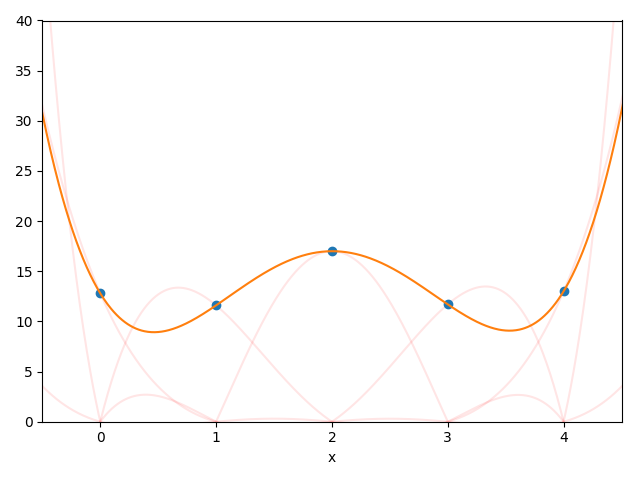



Das erste „richtige“ Modell, das wir uns anschauen, ist die Annäherung von Daten mit Polynomen. Wir wollen hierbei eine polynomielle Kurve finden, die nah an allen gemessenen Datenpunkten liegt. Dies kann man auf zwei Arten tun:
- Exakte Interpolation/Extrapolation: Man legt eine (entsprechend komplexe) Kurve genau durch alle gemessenen Datenpunkte.
- Approximative Interpolation/Extrapolation: Man legt eine (weniger komplexe) Kurve so gut wie möglich in die Nähe der Daten.
In beiden Fällen kann man die erhaltene Kurve entweder zwischen Datenpunkten ablesen — dann spricht man von Interpolation — oder rechts bzw. links vom Rand der Daten; dann nennt man es Extrapolation. Eigentlich ist das mathematisch also dieselbe Operation.
In dieser Aufgabe schauen wir uns die erste Option (exakte Interpolation mit Polynomen) an, die recht einfach zu realisieren ist. Die Approximation folgt darauf in der Teilaufgabe 1.4.
Zuerst wollen wir nun also ein Polynom finden, das genau durch eine eine Liste von gegebenen Punkten \[({\color{blue}x}_1,{\color{darkred}y}_1),({\color{blue}x}_2,{\color{darkred}y}_2),\dots,({\color{blue}x}_n,{\color{darkred}y}_n)\] verläuft. Für dieses Problem kann man relativ leicht eine direkte Lösung konstruieren.
Schauen wir uns dazu zuerst ein vereinfachtes Problem an: Ein Polynom \[{\color{red}p}({\color{darkblue}x}) = {\color{gray}a}_n{\color{darkblue}x}^n + {\color{gray}a}_{n-1}{\color{darkblue}x}^{n-1} + \dots + {\color{gray}a}_1{\color{darkblue}x} + {\color{gray}a}_0\] vom Grad \(n\) kann bis zu \(n\) verschiedene Nullstellen in \(\mathbb{R}\) besitzen.
Die Konstruktion eines Polynoms mit genau den Nullstellen \({\color{blue}x}_1,{\color{blue}x}_2,\dots,{\color{blue}x}_n\) ist dabei sehr einfach; das Polynom \[{\color{red}p}({\color{darkblue}x}) = \prod_{j=0}^n ({\color{darkblue}x}-{\color{blue}x}_j) = ({\color{darkblue}x} - {\color{blue}x}_1)\cdot({\color{darkblue}x} - {\color{blue}x}_2)\cdot\dots\cdot ({\color{darkblue}x}-{\color{blue}x}_n)\] erfüllt die gewünschte Bedingung. Überzeugen Sie sich selbst davon, dass dies ein Polynom der oben genannten Form ist.
Nun soll das Polynom an den Stellen \({\color{blue}x}_k\) nicht \(0\) betragen, sondern den Wert \({\color{darkred}y}_k\) haben. Die Lösung dazu sind die Lagrange-Polynome: Das Lagrange-Polynom zur Position \({\color{blue}x}_k\) ist definiert als \[{\color{red}\ell}_k({\color{darkblue}x}) = \prod_{\begin{smallmatrix}j=1\\j\neq k\end{smallmatrix}}^n \frac{{\color{darkblue}x}-{\color{blue}x}_j}{{\color{blue}x}_k-{\color{blue}x}_j}=\frac{{\color{darkblue}x}-{\color{blue}x}_1}{{\color{blue}x}_k-{\color{blue}x}_1}\cdots\frac{{\color{darkblue}x}-{\color{blue}x}_{k-1}}{{\color{blue}x}_k-{\color{blue}x}_{k-1}}\cdot\frac{{\color{darkblue}x}-{\color{blue}x}_{k+1}}{{\color{blue}x}_k-{\color{blue}x}_{k+1}}\cdots\frac{{\color{darkblue}x}-{\color{blue}x}_n}{{\color{blue}x}_k-{\color{blue}x}_n}. \]
Das Polynom, das unser Problem damit löst ist dann durch\[{\color{red}p}({\color{darkblue}x}) = {\color{darkred}y}_1\cdot {\color{red}\ell}_1({\color{darkblue}x}) + {\color{darkred}y}_2\cdot {\color{red}\ell}_2({\color{darkblue}x}) + \dots + {\color{darkred}y}_n\cdot{\color{red}\ell}_n({\color{darkblue}x}) \]
gegeben.- Zuerst wollen wir verstehen, warum die Lagrange-Polynome das Problem lösen. Betrachten Sie ein festes Lagrange-Polynom zu einer Stützstelle \({\color{blue}x}_k\) und bestimmen Sie die festen Werte \({\color{red}\ell}_k({\color{blue}x}_k)\) und \({\color{red}\ell}_k({\color{blue}x}_i)\) für eine andere Stützstelle \({\color{blue}x}_i \neq {\color{blue}x}_k\).
Theoriefrage: Erklären Sie in der Übung, warum das Lagrange-Polynom in der Tat unsere Aufgabe löst, d.h. ein Polynom von \((n-1)\)-tem Grad durch \(n\) Punkte \(\{({\color{blue}x}_i,{\color{darkred}y}_i)|i=1...n\}\) legt. - Um ein einfaches Polynom mittels Interpolation an die Daten zu legen, müssen wir (die meisten) Messwerte auslassen. Am einfachsten gelingt dies, indem wir in regelmäßigen Abständen Punkte herausgreifen.
- Starten sie mit einer sehr kleinen Menge von Teildaten (zwischen 2 bis 10 Punkte) und lassen Sie diese anzeigen.
Definieren sie zuerst ein Gitter von Stellen auf dem das Polynom ausgewertet wird (siehe im Skript unter Gitter;x = np.linspace(...)). - Formulieren Sie nun mithilfe von Numpy und dem Vektor
xdas oben beschriebene Polynom.
Fügen Sie das Ergebnis (die Funktionswerte ausgewertet an allen Stellen, an dem es echte Messwerte gibt) Ihrem Plot hinzu. Vergleichen Sie die Interpolation mit den tatsächlichen Daten. - Was fällt Ihnen auf wenn Sie die Anzahl der Punkte ändern durch die das Polynom verlaufen soll (und damit den Grad des Polynoms)? (Probieren Sie verschiedene Werte aus!)
Numpy-Tipp: Sofern Sie die vektorisierte Rechnung üben möchten, können sie versuchen den Nenner der jeweiligen Lagrange-Polynome in einer Zeile zu formulieren. (siehe Funktionennp.prod(...)undnp.delete(...)) - Starten sie mit einer sehr kleinen Menge von Teildaten (zwischen 2 bis 10 Punkte) und lassen Sie diese anzeigen.
- Fügen Sie Ihrem Plot die Lagrange-Polynome hinzu (zum Beispiel wie im obigen Bild als halbtransparente Kurven).
- Was passiert, wenn sie nun langsam die Anzahl der Datenpunkte vergrößern und schließlich „zu viele“ verwenden? Wie gut ist das Modell und wie gut hilft es uns bei der Vorhersage bzw. wie gut approximiert es den Verlauf der Wetterkurve selbst? Denken Sie Beispielsweise an Fehler oder Ungenauigkeiten in den Messungen oder auf Verallgemeinerungen (z.B. nächster Tag, nächste Woche oder nächstes Jahr).
Aufgabe 1.3: (Laufende) Mittelwerte
[15 Punkte]



(a) konstante Approximation
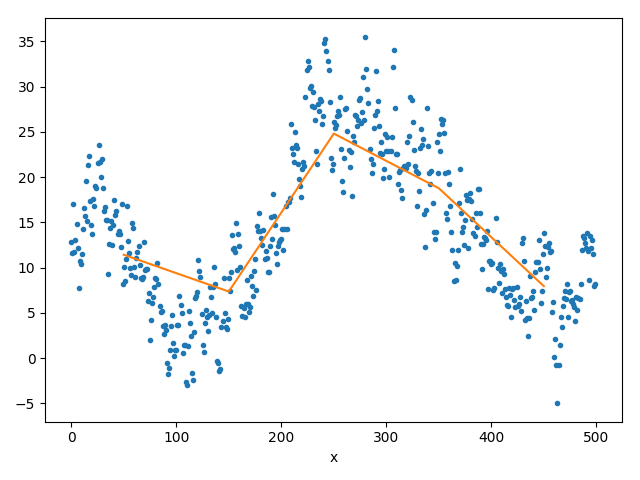



(b) stückweiser Mittelwert
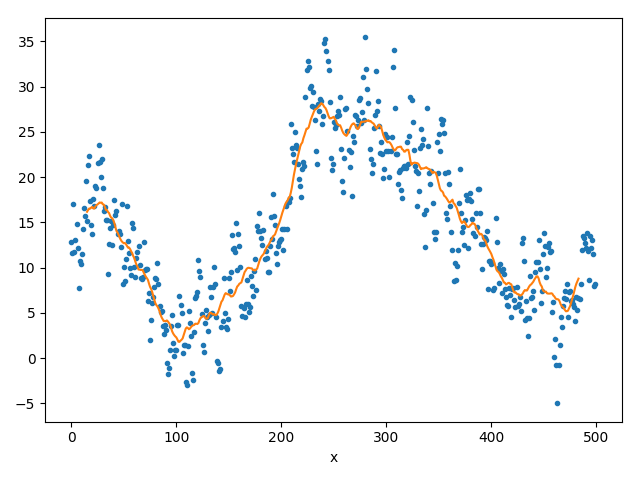



(c) laufender Mittelwert.
Interpolation ist eine interessante Methode, um den Zwischenraum zwischen den Punkten zu füllen. Allerdings hat dieser Ansatz, wie wir gesehen haben, so seine Tücken. Speziell die Polynominterpolation neigt zu „Überschwingung“. Mit anderen Funktionensystemen kann man dieses Problem mindern, aber es bleibt schwierig, die Komplexität des Modells an die Daten anzugleichen.
Daher probieren wir nun etwas (auf den ersten Blick) ganz anderes:
Wir bedienen uns des Mittelwertes \(\frac{1}{n}({\color{darkred}y}_1+{\color{darkred}y}_2+\dots +{\color{darkred}y}_n)\) von einer Reihe von Messwerten. Das liefert natürlich zunächst nur eine Zahl, aber mit ein bisschen Schieben (und später, in Aufgabe 1.5, einem allgemeineren Begriff von „Mittelwert“), bekommt man ein leistungsfähiges Verfahren, um Rauschen aus Daten zu entfernen (und damit brauchbare Vorhersagen zu machen).
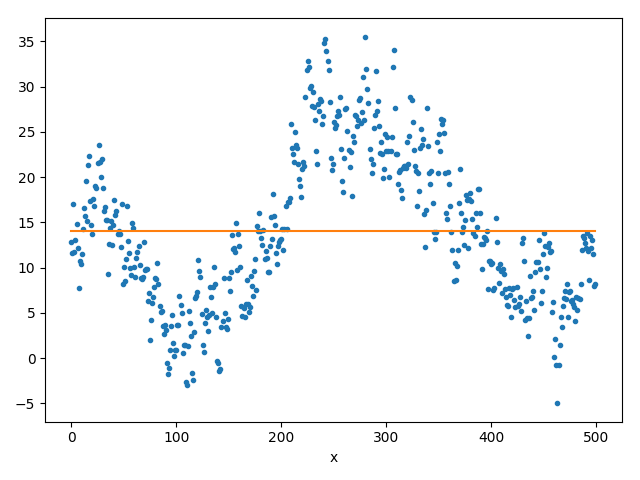
- Fügen Sie eine Linie auf Höhe des Mittelwertes Ihres Datensatzes Ihrem Plot hinzu (siehe Abbildung 3a).
Hinweis: Numpy bietet bereits eine Mittelwert-Funktion für Vektoren an. - Der Mittelwert selbst ist natürlich wenig aussagekräftig was den Verlauf des Datensatzes betrifft.
Daher überlegen wir uns ein verbessertes Schema:
Wir teilen den Datensatz in gleich große Teile ein, die jeweils \(m \ll n\) Messwerte enthalten. (Den letzten unvollständigen Teil können Sie dabei weglassen oder, noch besser, in ihrerfor-Schleife gesondert betrachten.
Nun bestimmen wir den Mittelwert jedes einzelnen Teils und Zeichnen den Verlauf der Mittelwerte (durch direkte Linien verbunden ein). Setzen sie dabei die x-Koordinate des jeweiligen Mittelwertes dabei auf die Mitte des betrachteten Teils (ein Ergebnis sieht man in Abbildung 3b).
Was fällt Ihnen auf, wenn sie die Größe der Teile verändern? Was sagt dies über das Modell aus?
Hinweis: Numpy bietet bereits eine Mittelwert-Funktion für Vektoren und eine Möglichkeit, Subvektoren zu extrahieren an. - Laufende Mittelwerte (engl.: „running averages“):
Was wir eben mit festen Teilen des Datensatzes gemacht haben können wir nun auch mit „mitlaufenden“ Teilen realisieren.
Bilden Sie hierzu immer den Mittelwert über ein kleines Fenster aus den Daten und verschieben sie dieses Fenster in 1er Schritten (immer einen Index hochzählen) über den gesamten Datensatz. Der gemittelte Wert muß auf der x-Achse immer in der Mitte des Fensters abgetragen werden.
Eine (noch) kontinuierliche(re) Kurve erhält man, wenn man diese Punkte noch, wie zuvor, mit Geraden verbindet.
Hinweis: Beachten Sie, dass ihre Kurve kleiner ist, als der Datensatz selbst. - Die Mittelwertbildung entfernt das Rauschen; dennoch bleibt die Kurve flexibler. Spielen Sie auch hier mit der Größe des Intervalls und beobachten Sie das Ergebnis.
Was fällt Ihnen auf? Wie gut ist das Modell und wie gut hilft es uns bei der Vorhersage bzw. wie gut approximiert es den Verlauf der Wetterkurve selbst?
Denken Sie Beispielsweise an Fehler oder Ungenauigkeiten in den Messungen oder auf Verallgemeinerungen (z.B. nächster Tag, nächste Woche oder nächstes Jahr).
Aufgabe 1.4: Regression — linear und polynomiell
[30 Punkte]
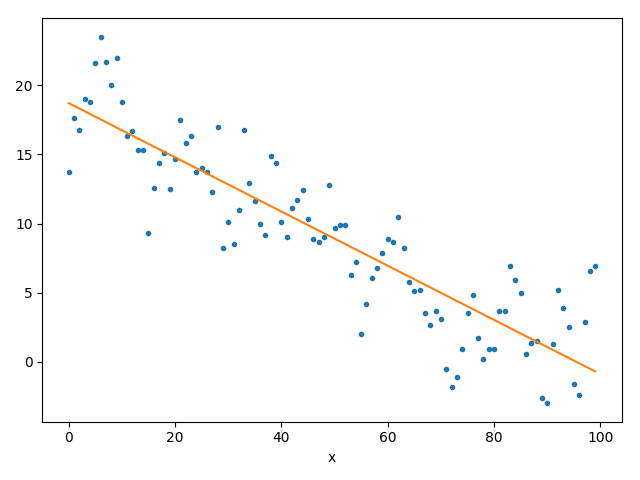



(a) lineare Regression
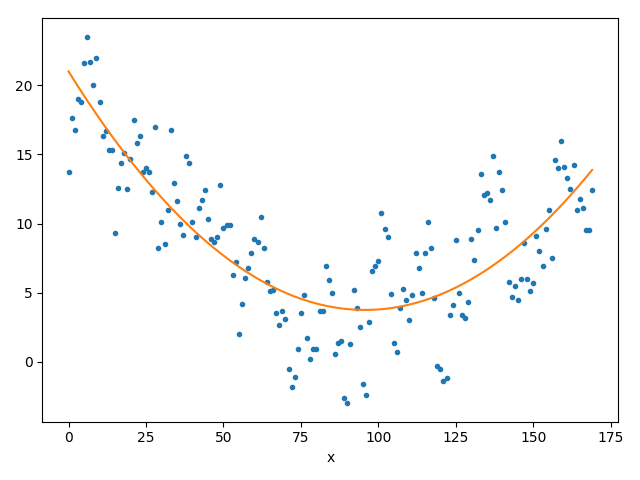



(b) Parabelfit
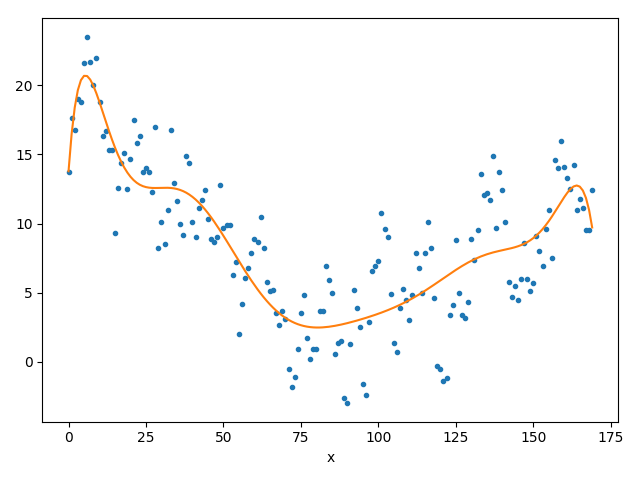



(c) Fit eines Polynoms vom Grad 10
Wir haben nun einige Ansätze gesehen:
- Polynominterpolation ist glatt, kann aber nur wenige Datenpunkte berücksichtigen.
- Laufenden Mittelwerte sind flexibler, haben aber andere Nachteile (siehe Fragen in der Aufgabe zuvor).
Mit unserem nächsten Ansatz Schema versuchen wir uns an einer etwas schwierigeren Methode, um ein Modell fitten. Die Rede ist von Regression, dem Finden einer Ausgleichskurve die möglichst nah an sehr vielen Daten liegt. Ist diese Kurve eine Grade, so spricht man von linearer Regression; handelt es sich um ein Polynom, so nennt man das ganze polynomielle Regression (oder auch Polynomregression).
Worum geht es?
In der letzten Aufgabe haben Sie bereits den Mittelwert des ganzen Datensatzes als Linie dargestellt. Mit einem solchen Modell gehen einige Einschränkungen einher. Zum Beispiel liefert es nicht direkt eine Tendenz (Anstieg oder Abstieg) der Werte. Eng damit verbunden ist auch, daß die Form der Kurve sich nicht sehr gut an die Daten anpasst. Wir beheben dies nun in zwei Schritten (der zweite folgt in Aufgabe 1.5).
Als erstes möchten wir nun eine Gerade \(y=mx+b\) finden, die unseren Wetterverlauf möglichst gut approximiert. Im folgenden zeigen wir Ihnen wie die Parameter \(m\) und \(b\) bestimmt werden können.
Wir verwenden die „Methode der kleinsten Quadrate“:
Zuerst definieren wir den qualitativen Fehler, den ein Modell mit festen Parametern hätte. \[\begin{aligned}
E({\color{darkblue}b},{\color{darkblue}m}) &= \sum_{i=1}^n \left( ( {\color{darkblue}m}{\color{blue}x}_i + {\color{darkblue}b} ) - {\color{blue}y}_i \right)^2\\
&= \sum_{i=1}^n \left( {\color{darkblue}b}^2 + {\color{blue}y}_i^2 + {\color{darkblue}m}^2{\color{blue}x}_i^2 + 2{\color{darkblue}b}{\color{darkblue}m}{\color{blue}x}_i - 2{\color{darkblue}b}{\color{blue}y}_i - 2{\color{darkblue}m}{\color{blue}x}_i{\color{blue}y}_i \right)
\end{aligned}
\]
Konkret messen wir hier den Unterschied zwischen dem geschätzten Wert \({\color{darkblue}m}{\color{blue}x}_i+{\color{darkblue}b}\) und dem tatsächlichen Wert \(y_i\) und quadrieren die Ergebnisse jeweils. Die Summe \(E({\color{darkblue}b},{\color{darkblue}m})\) der quadratischen Fehler gibt uns damit ein Maß für den Gesamtfehler zurück.
Wichtig: Bei dieser Regressionsaufgabe sind die Parameter \({\color{darkblue}m}\) und \({\color{darkblue}b}\) nicht fest, sondern die Punktpaare (Messwerte) \(({\color{blue}x}_1,y_1),\dots,({\color{blue}x}_n,y_n)\). Wenn wir diese Messwerte kennen, hängt die Funktion \(E\) nur noch von \({\color{darkblue}b}\) und \({\color{darkblue}m}\) ab; dies sind die Variablen, die wir optimieren wollen (so das der Fehler \(E\) so klein wie irgend möglich wird).
Wie in der Kurvendiskussion üblich, kann man lokale Extremwerte durch die Ableiten und Null setzen einer Funktion bestimmen: \[\left[ f'({\color{blue}x}) = 0 \text{ und } f''({\color{blue}x}) \neq 0 \right] \Rightarrow {\color{blue}x} \text{ ist lokales Extremum}
\]
Im Fall von \(E\) können wir sogar davon ausgehen, dass es genau ein globales Minimum gibt, d.h. es reicht aus die Nullstellen der Ableitung zu bestimmen (die Prüfung der zweiten Ableitung können wir ohne Bedenken ignorieren). Wir fassen also \(E\) einmal als Funktion abhängig von \({\color{darkblue}m}\) auf, und einmal als Funktion abhängig von \({\color{darkblue}b}\). Wir leiten \(E\) erst nach \({\color{darkblue}b}\) ab. \[\begin{aligned}
0 = E'({\color{darkblue}b}) &= \sum_{i=1}^n \left( 2{\color{darkblue}b} + 2{\color{darkblue}m}{\color{blue}x}_i - 2{\color{blue}y}_i \right)\\
&= 2{\color{darkblue}b}n + 2\sum_{i=1}^n \left( {\color{darkblue}m}{\color{blue}x}_i - {\color{blue}y}_i \right)\\
\end{aligned}
\] also \[\begin{aligned}
{\color{darkblue}b} &= \sum_{i=1}^n \frac{1}{n}\left({\color{blue}y}_i - {\color{darkblue}m}{\color{blue}x}_i \right)\\
&= \bar{{\color{blue}y}} - {\color{darkblue}m}\cdot \bar{{\color{blue}x}},
\end{aligned}
\] für die Mittelwerte \(\bar{{\color{blue}x}} := \frac{1}{n}\sum_{i=1}^n{\color{blue}x}_i\) und \(\bar{{\color{blue}y}} := \frac{1}{n}\sum_{i=1}^n{\color{blue}y}_i\).
Jetzt leiten wir nach \({\color{darkblue}m}\) ab:
\[\begin{aligned}
0 = E'({\color{darkblue}m}) &= \sum_{j=1}^n \left( 2{\color{darkblue}m}{\color{blue}x}_j^2 + 2{\color{darkblue}b}{\color{blue}x}_j - 2{\color{blue}x}_j{\color{blue}y}_j \right)\\
&= 2{\color{darkblue}m}\sum_{j=1}^n {\color{blue}x}_j^2 + 2{\color{darkblue}b}\sum_{j=1}^n {\color{blue}x}_j - 2\sum_{j=1}^n {\color{blue}x}_j{\color{blue}y}_j\\
&= 2{\color{darkblue}m}\sum_{j=1}^n {\color{blue}x}_j^2 + 2n{\color{darkblue}b}\cdot \bar{\color{blue}x} - 2 \sum_{j=1}^n {\color{blue}x}_j{\color{blue}y}_j
\end{aligned}
\] Wir bringen \({\color{darkblue}b}\) auf eine Seite der Gleichung setzen Sie mit dem vorherigen Ergebnis gleich.
\[\begin{aligned}
\frac{-{\color{darkblue}m}\sum_{j=1}^n {\color{blue}x}_j^2 + \sum_{j=1}^n {\color{blue}x}_j{\color{blue}y}_j}{n\cdot \bar{\color{blue}x}} &= \bar{\color{blue}y} - {\color{darkblue}m}\cdot \bar{{\color{blue}x}} \\
\Leftrightarrow \qquad {\color{darkblue}m}\left(\bar{\color{blue}x} - \frac{\sum_{j=1}^n{\color{blue}x}_j^2}{n\cdot\bar{\color{blue}x}} \right) &= \bar{\color{blue}y} - \frac{\sum_{j=1}^n {\color{blue}x}_j{\color{blue}y}_j}{n\cdot\bar{\color{blue}x}}\\
\Leftrightarrow \qquad {\color{darkblue}m} &= \frac{n\bar{\color{blue}x}\cdot \bar{\color{blue}y} - \sum_{j=1}^n {\color{blue}x}_j{\color{blue}y}_j}{n\bar{\color{blue}x}^2 - \sum_{j=1}^n{\color{blue}x}_j^2}\\
\end{aligned}
\]
zu bearbeitenden Aufgaben
- Implementieren Sie die lineare Regression in Python. Sie können die o.g. Formeln direkt verwenden. Hier können Sie ruhig den ganzen Datensatz verwenden.
Hinweis zur Darstellung: Es reicht wenn sie den Funktionswert für \({\color{darkblue}m}x+{\color{darkblue}b}\) für den ersten und letzten Datensatzeintrag bestimmen und diese beiden Punkte dann durch eine durchgezogene Linie verbinden.
Numpy-Tipp: Die Koeffizienten \({\color{darkblue}m}\) und \({\color{darkblue}b}\) können mithilfe von Numpy in je einer Zeile berechnet werden! - Theoriefrage (etwas anspruchsvoller): Überlegen Sie sich ein ähnliches Schema für quadratische Polynome (Parabeln). Starten Sie wieder mit einer ähnlichen (quadratischen) Formel, die minimiert werden soll.
Wir suchen nun also die Koeffizienten \({\color{darkblue}a},{\color{darkblue}b},\color{darkblue}c\) des Polynoms \({\color{darkblue}a}x^2 +{\color{darkblue}b}x +\color{darkblue}c\), die die Gleichung minimieren — was wir suchen ist also ein lokales Minimum (tatsächlich ist es sogar ein globales Minimum). Betrachten sie die Koeffizienten nacheinander als Variablen und leiten Sie nach diesen ab. Die drei dabei entstehenden Gleichungen bilden ein Gleichungssystem. Lösen Sie dieses auf dem Papier, um die Lösung für \({\color{darkblue}a}, {\color{darkblue}b}\) und \(\color{darkblue}c\) zu erhalten.
Erweitern Sie nun Ihr Programm durch die Möglichkeit, ein quadratisches Polynom an den Datensatz zu fitten. - Selbstverständlich geht dies auch für höhere Polynomgrade. Die Lösung der Gleichung mit Mitteln der Schulmathematik wird allerdings mühsam — hier kommt man viel schneller voran mit Mitteln der linearen Algebra, die wir erst später genauer diskutieren.
Daher (und auch um den Zeitrahmen nicht zu sprengen), nutzen wir dafür jetzt fertigen Code:
Glücklicherweise bietet Numpy bereits eine Funktion an, die Polynome beliebigen Grades quadratisch fittet —numpy.polyfit(...). Die Funktion liefert direkt die Koeffizienten eines Polynoms beliebigen Grades (kann man frei auswählen) das gegen Daten gefittet wurde (die Funktion ist recht flexibel — siehe Doku. Für unsere Aufgabe kann man einfach alle optionalen Parameter weglassen; dann bekommt man genau das, was wir brauchen).
Implementieren Sie nun Polynomfits beliebigen Grades mit Hilfe der Bibliotheksfunktion.
Experimentieren Sie mit verschiedenen Graden — was beobachten Sie?
Verwendung derPolyfit-Funktionx = ... # liste oder numpy arrays y = ... # -"- (bilden zusammen Punkteliste (x[i],y[i]) ) coeff = np.polyfit(x,y,5) # 5 ist hier der Polynomgrad des fits # coeff enthält die Liste der Koeffizienten des gefitteten Polynoms p = np.poly1d(coeff) # np.poly1d erstellt daraus eine vektorisierte Funktion p(np.linspace(0,1,10)) # Auswertung von p an den stellen 0,0.1,0.2,0.3, ...
Aufgabe 1.5: Moving Least Squares
[15 Punkte]
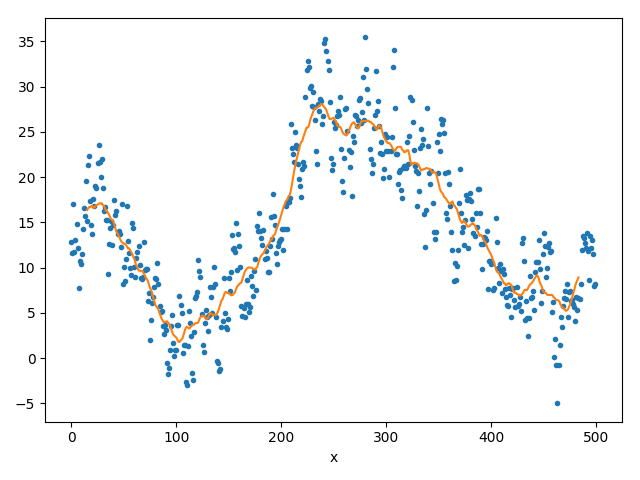



Unsere bisherigen Methoden sind nicht so wirklich zufriedenstellend:
- Die Polynominterpolation/approximation explodiert gerne, wenn Sie zu flexibel wird; man kann Sie nur mit geringem Grad einsetzen.
- Der laufenden Mittelwert liefert flexible Kurven, hat aber Schwierigkeiten mit Vorhersagen und mit der Genauigkeit eben dieser.
Im letzten Schritt kombinieren wir daher beide Verfahren, um die Stärken beider Verfahren zu vereinen.
Damit erhält man das (berühmte) „Moving-Least-Squares“-(MLS)-Verfahren, welches in der modernen maschinellen Datenanalyse (in den letzten Jahren) sehr populär geworden ist.
Die Vorgehensweise ist prinzipiell genauso wie beim „mitlaufenden“ Mittelwert; allerdings ersetzen wir die Bildung eines einfachen Mittelwertes mit polynomieller Regression:
- Wieder definieren wir einen Teildaten-Abschnitt (Fenster), wenden darauf die Regression (linear, quadratisch oder am besten den allgemeinen Polynomfit aus NumPy) an.
- Anstatt den einfachen Mittelwert in der Mitte des Fensters abzutragen werten wir nun das erhaltene Regressionspolynom in der Mitte des Fensters aus.
- Danach verschieben wir das Fenster um eine Stelle und wiederholen die Prozedur — ganz ähnlich wie beim laufenden Mittelwert.
Implementieren Sie nun die beschriebene Moving-Least-Squares Methode für Polynome mit allgemeinem Grad mithilfe der polyfit-Methode.
(Falls Sie den Teil in der vorherigen Aufgabe nicht lösen konnten: Nutzen Sie statt dessen den linearen bzw. den quadratischen Ansatz).
Analyse: Testen Sie die Methoden mit verschiedenem Polynomgrad und verschiedener Fensterbreite.
Die besten Ergebnisse erhält man, wenn man den Grad des Polynoms nicht zu hoch wählt (max. einstellig).
Was sind Ihre Beobachtungen? Erklären Sie diese!
Aufgabe 2: Cross-Validation
Zuletzt wollen wir bewerten, wie gut das Modell ist, dass wir gefittet haben.
Dazu messen wir, wie genau die Voraussagen des Modells sind. Wichtig hierbei ist, dass man für die Validierung für solche Daten, die wir beim Bauen (z.B. via Regression) des Modells noch nicht verwendet haben). Zuerst müssen wir also den Fehler eines Modells quantifizieren.
Eine Möglichkeiten dafür (von sehr vielen) haben wir bereits (in leicht anderer Form) kennengelernt — die Auswertung des mittleren quadratischen Fehlers: \[ E({\color{darkblue}b},{\color{darkblue}m}) = \frac{1}{n}\sum_{i=1}^n \left( ( \mathcal{M}({\color{darkblue}x}_i) ) - {\color{darkblue}y}_i \right)^2. \] Was wir hier hinzugefügt haben, ist die Mittelwertbildung (Division durch die Anzahl von Punkten, an denen validiert wird); dies macht das Maß unabhängig von der Menge an Validierungsdaten.
Hierbei bezeichne \(\mathcal{M}\) unser bestimmtes Modell und \(\mathcal{M}({\color{darkblue}x}_i)\) den Funktionswert an der Stelle \({\color{darkblue}x}_i\).
Nun möchten wir jedoch das Modell nicht an den Stützstellen auf die Qualität Prüfen an denen wir das Modell gefittet haben. Die Qualität eines Modells zeichnet sich dadurch aus, wie gut es auf Fälle verallgemeinert, die bei der Erstellung des Modells noch nicht in betrachtet wurden. In der Formel oben sind die Indizes daher so zu verstehen, daß hier nur „neue“ Daten angeschaut werden (nicht die, die für das ursprüngliche „Fitting“ genutzt wurden). Es gibt zwei Varianten für die Validierung: Grundsätzlich teilen wir den Datensatz in zwei Teile train und test auf. Nun können wir entweder die Genauigkeit beim Interpolieren (kleine Lücken in den Daten) messen, oder die Genauigkeit beim Extrapolieren (große Lücken bzw. Vorhersagen in Zukunft oder ungemessene Vergangenheit).
- Interpolation: Teilen Sie den Datensatz rein zufällig in
trainundtestauf. Nutzen Sie die Hälfte der Daten für das Training, die andere Hälfte für den „Test“-Teil (Vorsicht: Wenn man einen Teil der Punkte auswählt, müssen natürlich jeweils x und y-Koordinate gemeinsam ausgewählt werden.) Vermischen sie dazu den Datensatz zuerst und „slicen“ Sie dann eine Teilmenge der richtigen Größe aus. (Siehe Skript zunp.random.permutation(...)) - Extrapolation: Lassen Sie beim „Training“ nur Daten am Ende weg (z.B. für einen Tag, eine Woche, oder länger). Diese Daten bilden den Testteil.
Im Folgenden können wir eine der beiden Varianten auswählen (Geschmackssache, was interessanter ist).
Aufgaben
[15 Punkte]
Bearbeiten Sie nun folgende Aufgaben!
- Implementieren Sie eine der beiden Varianten (Dateninterpolation oder Extrapolation, also Wettervorhersage).
- Nutzen Sie nun Ihren Code zu allen Modellen, die sie an einer beliebigen Stelle auswerten können (Aufgabe 1.2 und 1.4; optional auch Aufgabe 1.5).
„Trainieren“, d.h. fitten Sie die jeweiligen Modelle auf dem Teiltrain.
Achtung: Beachten Sie auch hier wieder, dass die x-Werte zu den y-Werten passen, also dasstrain_y[k]zum richtigentrain_x[k]gehören muß. - Werten Sie die Modelle nun auf den
test-Teilen aus. Das bedeutet: Messen Sie die Qualität mithilfe der oben genannten Qualitätsfunktion, aber verwenden Sie nur die Punkte aus dem Test-Teil. - Unser Ziel ist es, die Modelle anhand dieser Definition von Qualität zu vergleichen. Momentan hängt das Ergebnis jedoch von der zufälligen Aufteilung der beiden Datensatzteile ab (bzw.: Bei der Extrapolation kommt man für verschiedene Vorhersagebereiche zu unterschiedlichen Ergebnissen). Daher sollte man die Validierung mehrmals durchführen und über die Ergebnisse mittelt (also mehrmals unabhängig voneinander zufällig aufteilen, oder verschiedene Wochen zur Vorhersage auswählen, mit der Vorwoche oder dem Vormonat als Trainingsdaten).
- Führen Sie die Validierung für verschiedene Parameter (verschiedener Polynomgrad bzw. zusätzlich auch noch verschiedener Fenstergröße beim optionalen MLS) durch und plotten Sie den entsprechenden Validierungsfehler. Welche Parameter funktionieren am besten, und warum?